Ответы к 2 кол

1

Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону. Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением x = xm cos (ωt + φ0). Здесь x – смещение тела от положения равновесия, xm – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время.

Графическое представление колебаний: ускорение и скорость гармонических колебаний.

При колебательном движении тела вдоль прямой линии (ось OX) вектор скорости направлен всегда вдоль этой прямой. Скорость υ = υ_x движения тела определяется выражением 

Для гармонического закона движения  Вычисление производной приводит к следующему результату: 

следовательно, ускорение a равно производной функции υ (t) по времени t, или второй производной функции x (t). Вычисления дают: 

Дифференциальное уравнение гармонических колебаний.

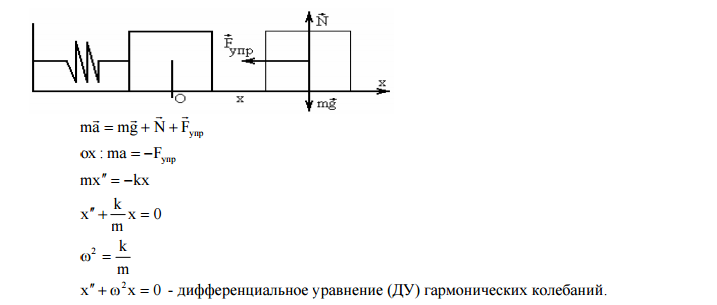
Энергия при гармонических колебаниях.

Потенциальная энергия U тела, смещенного на расстояние х от положения равновесия, измеряется той работой, которую произведет возвращающая сила  , перемещая тело в положение равновесия.

Кинетическая энергия

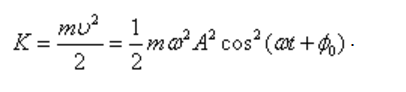
Полная энергия

2

Гармонический осциллятор.

Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):

F = -k x \,

где k — коэффициент жёсткости системы.

Получите формулы для нахождения периода колебаний: пружинного маятника;

m — масса груза, k — жёсткость пружины.

физического маятника,

где J — момент инерции маятника относительно оси вращения, m — масса маятника, l — расстояние от оси вращения до центра масс.

математического маятника.

где l — длина подвеса (к примеру, нити), g — ускорение свободного падения.

Колебательный контур.

2

Воспользовавшись II законом Ньютона, получите дифференциальное уравнение для свободных затухающих колебаний и проанализируйте его решение. В случае упругих колебаний возвращающая сила F = -kx. Если нет других сил, кроме упругой силы, то колебания называют свободными. Согласно второму закону Ньютона

, или . Разделим оба слагаемых на m:

(7.7)

Последнее соотношение носит название основного уравнения гармонических свободных колебаний. Общее решение этого уравнения имеет вид

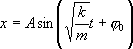
Запишите закон изменения амплитуды затухающих колебаний и поясните графиком.     Коэффициент затухания β. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону . Пусть за время τ амплитуда колебаний уменьшится в «e » раз («е» – основание натурального логарифма, е ≈ 2,718). Тогда,  с одной стороны, , а с другой стороны,  расписав амплитуды А_зат.(t) и А_зат.(t+τ), имеем

 

.

 

Из этих соотношений следует  βt = 1, отсюда .

Промежуток времени τ, за который амплитуда уменьшается в «е» раз, называется временем релаксации. Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.

В чем физический смысл коэффициента затухания?

логарифмический декремент затухания - безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.

огарифмического декремента?

Логарифми́ческий декреме́нт колеба́ний (декреме́нт затуха́ния; от лат. decrementum — «уменьшение, убыль») — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины x в одну и ту же сторону.

времени релаксации?

Время релаксации — промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в раз:

добротности?

Добротность колебательной системы-отношение энергии, запасённой в колебательной системе, к энергии, теряемой системой за один период колебания.

4

Вынужденные колебания.

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

Воспользовавшись II законом Ньютона, получите дифференциальное уравнение для вынужденных механических колебаний.

От чего зависит амплитуда вынужденных колебаний?

Амплитуда вынужденных колебаний  величины действующей силы, но и от ее частоты. Амплитуда вынужденных колебаний очень резко возрастает, если частота внешней силы близка к частоте собственных колебаний.

При каких условиях возникает резонанс?

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — явление, при котором амплитуда вынужденных колебаний имеет максимум при некотором значении частоты вынуждающей силы. Часто это значение близко к частоте собственных колебаний, фактически может совпадать, но это не всегда так и не является причиной резонанса.

Нарисовав 2-3 резонансных кривых, свяжите добротность колебательной системы с каждой из них.

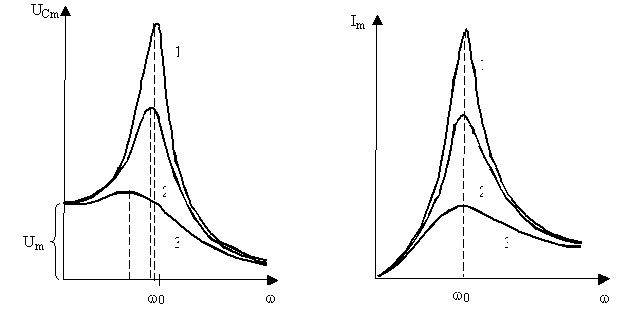
Что является источником любой волны?

Источник любой волны является колеблющееся тела, которые создают в окружающем пространстве деформацию среды.

Что такое волновой процесс?

Волновой процесс (волна)—это процесс распространения колебаний в сплошной среде. Сплошная среда — непрерывно распределенная в пространстве и обла­дающая упругими свойствами.

Какие волны называются продольными? поперечными?

Поперечная волна это когда направление колебаний перпендикулярно направлению распространения. В продольных волнах направление колебаний совпадает с направлением распространения волны.

От чего зависит скорость звука?

Скорость распространения звуковой волны (скорость звука) в среде зависит от массы молекул или атомов и расстояния между ними. А они в свою очередь зависят от химического состава вещества, его температуры, а для газов и давления.

Что такое волновой фронт? волновая поверхность?

Волновая поверхность - геометрическое место точек, колеблющихся в одинаковой фазе. Если источником волны является точка, то волновые поверхности в однородном и изотропном пространстве представляют собой концентрические сферы.

А Волновой фронт - это поверхность, до которой дошли колебания к данному моменту времени. Волновой фронт является частным случаем волновой поверхности.

запишите уравнение плоской волны.

.   

W - смещение любой из точек с координатой х в момент времени

k- волновое число  ,   

Каковы характерные особенности стоячей волны по сравнению с бегущей?

Стоя́чая волна́ — колебания в распределенных колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на прямую.

Главное отличие от бегущей волны заключается в том, что в стоячей волне не происходит переноса энергии, а лишь перекачка одного вида энергии в другой (как в колебаниях) . Например, электрической энергии в магнитную, кинетической — в потенциальную и т. п. Частота при этом по сравнению с прямой волной удваивается.

Получите уравнение стоячей волны.

Уравнение стоячей волны

Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:

Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны:

Преобразовав это уравнение, получим упрощенное уравнение стоячей волны:

От чего зависит амплитуда стоячей волны?

от координаты

от плотности среды

от амплитуды бегущей волны

от длины волны

Чему равно расстояние между двумя соседними пучностями стоячей волны? двумя соседними узлами?

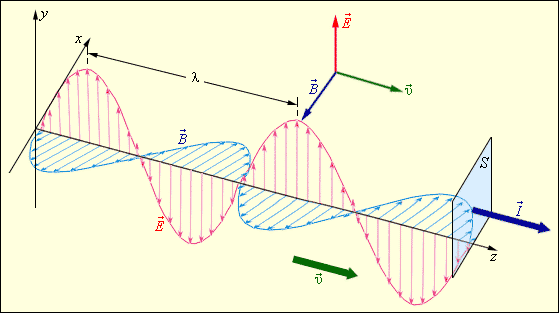
Поперечность электромагнитных волн.

Электромагнитные волны являются поперечными волнами. Это означает, что векторы Е и В электромагнитного поля волны перпендикулярны направлению ее распространения. Колебания напряженности электрического поля волны, выходящей из рупора, происходят в определенной плоскости, а колебания вектора магнитной индукции — в плоскости, ей перпендикулярной. Волны с определенным направлением колебаний называются поляризованными. На рисунке 3.5.6.4 изображена такая поляризованная волна. Приемный рупор с детектором принимает только поляризованную в определенном направлении волну.

Запишите дифференциальное уравнение электромагнитной волны.

Объемная плотность энергии электромагнитных волн.

Объемная плотность энергии w электромагнитной волны складывается из объемных плотностей и электрического и магнитного полей:

В чем физический смысл вектора Умова-Пойнтинга?

Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, компоненты которого входят в состав компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:

Шкала электромагнитных волн.

Интерференция света.

Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

Когерентность света.

взаимная согласованность протекания во времени световых колебаний в разных точках пространства и (или) времени, характеризующая их способность к интерференции. В общем случае световые колебания частично когерентны и количественно их когерентность измеряется степенью взаимной когерентно с-т и (с. в. к.), к-рая определяет контраст интерференционной картины (и. к.) в том или ином интерференц. эксперименте.

Условия максимума и минимума при интерференции.

Дифракция света.

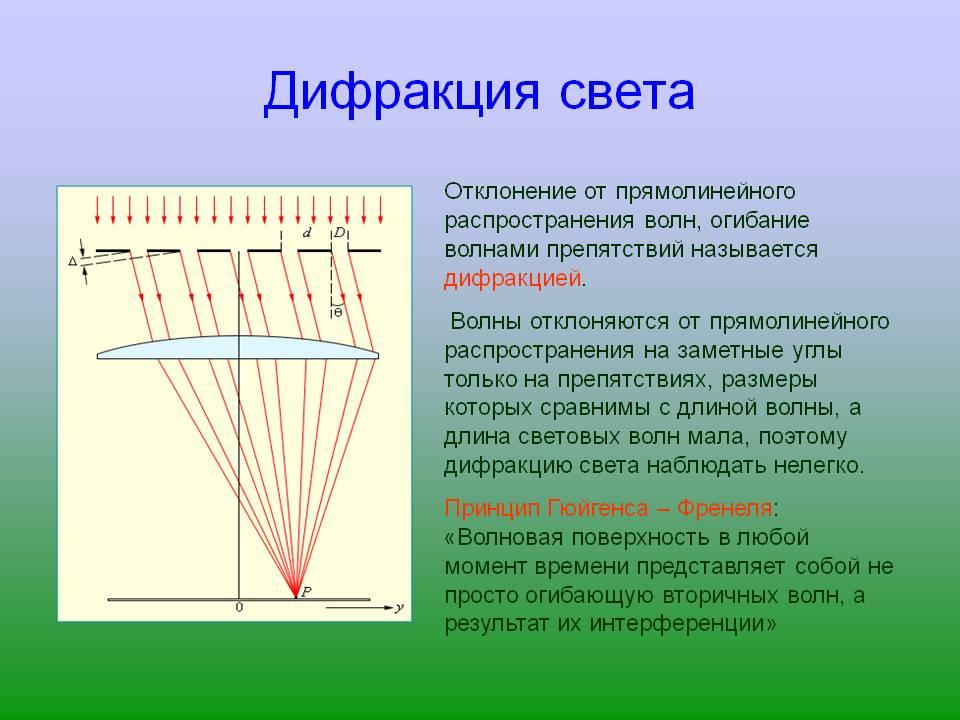
Условия наблюдения дифракции.

либо размеры препятствий (или отверстий) должны быть очень малыми, либо расстояние от препятствия до наблюдаемой картины должно быть велико.

Принцип Гюйгенса-Френеля.

Согласно принципу Гюйгенса-Френеля световая волна, возбуждаемая каким-либо источником S может быть представлена как результат суперпозиции когерентных вторичных волн. Каждый элемент волновой поверхности S (рис.) служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS.

Метод зон Френеля. Свойства зон Френеля.

Зонная пластинка.

Зонная пластинка — плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями, радиус которых совпадает с радиусами зон Френеля. Зонная пластинка «выключает» чётные либо нечётные зоны Френеля, чем исключает взаимную интерференцию (погашение) от соседних зон, что приводит к увеличению освещённости точки наблюдения. Таким образом, зонная пластинка действует как собирающая линза.

Также зонная пластинка представляет собой простейшую голограмму — голограмму точки.

Дифракция Фраунгофера на плоской щели при нормальном падении света.

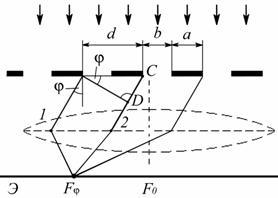
Дифракция Фраунгофера на дифракционной решетке

Дисперсия света.

Диспе́рсия све́та (разложение света) — это совокупность явлений, обусловленных зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимостью фазовой скорости света в веществе от частоты (или длины волны). Экспериментально открыта Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее.

Нормальная и аномальная дисперсия.

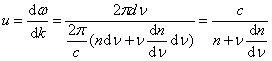 .  Отсюда можно записать:

.

(10.2.3)

Таким образом, при нормальной дисперсии   u < υ   и   .

При аномальной дисперсии  u > υ,  и, в частности, если  , то u > c. 

Поляризация света.

Естественный и поляризованный свет. Закон Малюса.

Закон Брюстера.

Зако́н Брю́стера — закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения.

Двойное лучепреломление.

Двойно́е лучепреломле́ние — эффект расщепления в анизотропных средах луча света на две составляющие. Впервые обнаружен датским учёным Расмусом Бартолином на кристалле исландского шпата в 1669 году. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча.

Поляризаторы.

Поляриза́тор —- устройство, предназначенное для получения полностью или частично поляризованного оптического излучения из излучения с произвольным состоянием поляризации. В соответствии с типом поляризации, получаемой с помощью поляризаторов, они делятся на линейные и круговые.