50. Характеристики статистического распределения: характеристики положения; характеристики формы; характеристики рассеяния.

Для выборки можно определить ряд числовых характеристик, которые аналогичны основным числовым характеристикам случайных величин в теории вероятностей (математическое ожидание, дисперсия , среднее квадратическое отклонение, мода, медиана) и являются в некотором смысле (который будет ясен дальше) их приближенным значением.

Пусть дано статистическое распределение выборки объема n для частот и относительных частот:

xi	x1	x2	…	xk
ni	n1	n2	…	nk

xi	x1	x2	…	xk
wi	w1	w2	…	wk

Выборочным средним называется среднее арифметическое значение всех вариант:

.

Если внести множитель под знак суммы, то получим формулу для выборочного среднего через относительные частоты:

.

Отметим, что в случае интервального ряда выборочное среднее вычисляется по тем же формулам, если в качестве чисел х₁, … , х_k взять середины интервалов: , … ,.

Выборочной дисперсией называется среднее арифметическое квадратов отклонений значений выборки от их выборочного среднего:

.

Снова внося множитель под знак суммы, получим формулу для выборочной дисперсии через относительные частоты:

.

Несложные преобразования приводят к более удобной формуле для вычисления выборочной дисперсии

,

где есть выборочное среднее квадрата изучаемой случайной величины, т.е.

.

Если выборка представлена интервальным статистическим рядом, то формулы для выборочной дисперсии остаются те ми же, где, как обычно, в качестве чисел х₁, … , х_k берутся середины интервалов: , … ,.

Выборочным средним квадратическим отклонением называется квадратный корень из выборочной дисперсии

.

Размахом вариации R называется разность между максимальным и минимальным значением в выборке. Если варианты в выборке ранжированы (размещены в возрастающем порядке), то

.

Коэффициент вариации определяется по формуле

.

Модой М_о вариационного ряда называется вариант, имеющий наибольшую частоту (или относительную частоту).

Медианой М_е вариационного ряда называется число, являющееся его серединой. Для дискретного ряда с нечетным числом вариант медиана равна его серединному варианту. Если же число вариант четно, то Медина равна среднему (т.е. полусумме) двух серединных вариант.

К основным статистическим характеристикам ряда измерений (вариацион­ного ряда) относятся характеристики положения(средние характе­ристики, или центральная тенденция выборки); характеристики рассеяния(ва­риации, или колеблемости) и характеристики формыраспределения.

К характеристикам положения относятся среднее арифметическое значе­ние (среднее значение), мода и медиана.

К характеристикам рассеяния (вариации, или колеблемости) относятся: размах вариации, дисперсия, среднее квадратическое (стандартное) отклонение, ошибка средней арифметической (ошибка средней), коэффициент вариации и др.

К характеристикам формы относятся коэффициент асимметрии, мера ско­шенности и эксцесс.

51. Оценка параметров генеральной совокупности. Точечная и интервальная оценка. Доверительный интервал. Уровень значимости

Оценка параметров генеральной совокупности

Существуют точечные и интервальные оценки генеральных параметров.

Точечной называют оценку, которая определяется одним числом. К таким оценкам относятся, например,

• выборочная средняя , или для сгруппированного вариационного ряда;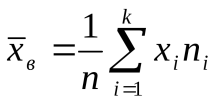

• выборочная дисперсия, или для сгруппированного вариационного ряда, или;

• выборочное среднее квадратическое отклонение и др.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны быть:

• несмещенными;

• эффективными;

• состоятельными.

Оценка называется несмещенной, если математическое ожидание ее выборочного распределения совпадает со значением генерального параметра.

Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками, т.е. обнаруживает наименьшую случайную вариацию.

Точечная оценка называется состоятельной, если при увеличении объема выборочной совокупности она стремиться к величине генерального параметра.

Например, выборочная средняя есть состоятельная, несмещённая оценка генеральной средней. Для выборки из нормальной генеральной совокупности эта оценка является также и эффективной.

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами – концами интервала – доверительного интервала.

Интервальные оценки позволяют установить точность и надежность оценок.

Для оценки генерального параметра с помощью доверительного интервала необходимы три величины:

• значение выборочного показателя;

• критерий надежности 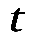, или показатель безошибочных прогнозов, значение которого определяется заранее, при планировании исследования, исходя из представления о большей или меньшей ответственности возможных результатов работы;

• ошибка репрезентативности или показатель точности выборочного параметра определяется на основе выборочных данных по формулам математической статистики.

Например, доверительный интервал для генеральной средней находится по формуле:при уровне значимости.

Доверительный интервал — термин, используемый в математической статистике при интервальной оценке статистических параметров, более предпочтительной при небольшом объёме выборки, чем точечная.

Уровень значимости - это вероятность того, что мы сочли различия существенными, а они на самом деле случайны.

Когда мы указываем, что различия достоверны на 5%-ом уровне значимости, или при р<0,05, то мы имеем виду, что вероятность того, что они все-таки недостоверны, составляет 0,05.

Когда мы указываем, что различия достоверны на 1%-ом уровне значимости, или при р<0,01, то мы имеем в виду, что вероятность того, что они все-таки недостоверны, составляет 0,01.

Если перевести все это на более формализованный язык, то уровень значимости - это вероятность отклонения нулевой гипотезы, в то время как она верна.

Ошибка, состоящая в той, что мы отклонили нулевую гипотезу, в то время как она верна, называется ошибкой 1 рода.(См. Табл. 1)

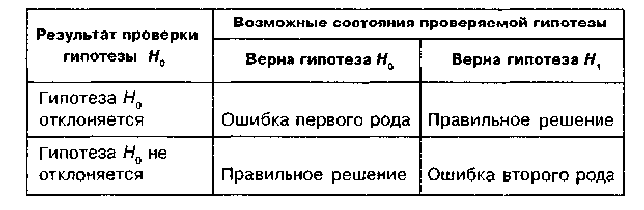Табл. 1. Нулевая и альтернативные гипотезы и возможные состояния проверки.

Вероятность такой ошибки обычно обозначается как α. В сущности, мы должны были бы указывать в скобках не р<0,05 или р<0,01, а α<0,05 или α<0,01.

Если вероятность ошибки - это α, то вероятность правильного решения: 1—α. Чем меньше α, тем больше вероятность правильного решения.

Исторически сложилось так, что в психологии принято считать низшим уровнем статистической значимости 5%-ый уровень (р≤0,05): достаточным – 1%-ый уровень (р≤0,01) и высшим 0,1%-ый уровень (р≤0,001), поэтому в таблицах критических значений обычно приводятся значения критериев, соответствующих уровням статистической значимости р≤0,05 и р≤0,01, иногда - р≤0,001. Для некоторых критериев в таблицах указан точный уровень значимости их разных эмпирических значений. Например, для φ*=1,56 р=О,06.

До тех пор, однако, пока уровень статистической значимости не достигнет р=0,05, мы еще не имеем права отклонить нулевую гипотезу. Мы будем придерживаться следующего правила отклонения гипотезы об отсутствии различий (Но) и принятия гипотезы о статистической достоверности различий (Н₁).