2.3.8. Расчет сложных газопроводов
Простым газопроводом принято называть
газопровод постоянного диаметра, по
которому транспортируется газ с
неизменным расходом Q.
Газопроводы, отличающиеся от указанных
условий, называются сложными.
Любая сложная система газопроводов
может быть разделена на элементарные
участки, размеры которых (Li,
Di) и
производительности (Qi)
являются исходными данными для
расчета системы в целом. При этом в
узловых точках должны выполняться
следующие условия: равенство давлений,
сохранение массы газа и его теплосодержания.
Такой поэтапный метод расчета весьма
трудоемок, но достаточно просто
реализуется с помощью ЭВМ.
Нормами технологического проектирования
допускается в первом приближении с
достаточной для практических расчетов
точностью заменять сложный газопровод
эквивалентным простым, который имеет
такую же пропускную способность при
аналогичных граничных условиях, что и
простой газопровод.
При гидравлическом расчете сложного
газопровода (как и простого) решается
одна из задач:
определение пропускной способности Qпри заданных начальном и конечном
давлениях и геометрических размерах
участков (Li,
Di);
определение конечного давления при
заданных расходах и геометрических
размерах участков;
определение диаметров отдельных
участков по заданным перепаду давления
и расходам для участков известной
длины.
Для расчета сложных газотранспортных
систем применяются следующие способы:
замена сложного газопровода эквивалентным
простым газопроводом (применяется при
отсутствии сбросов и подкачек);
замена сложного газопровода с различными
расходами по участкам эквивалентным
простым газопроводом с постоянным
эквивалентным расходом (применяется
в случае сбросов и подкачек газа).
Рассмотрим наиболее часто встречающиеся
случаи.
Однониточный газопровод с участками различного диаметра
Р ассмотрим
однониточный газопровод с участками
различного диаметра (рис.2.11).
ассмотрим
однониточный газопровод с участками
различного диаметра (рис.2.11).
Рис. 2.11. Схема сложного
однониточного газопровода
Воспользуемся формулой для определения
пропускной способности простого
газопровода
 .(2.84)
.(2.84)
Тогда из выражения (2.84)
очевидно соотношение
 .(2.85)
.(2.85)
Исходя из определения эквивалентного
газопровода, предполагающего равенство
температуры и давления газа в начале и
в конце реального и эквивалентного
газопровода, можно записать
 ,(2.86)
,(2.86)
откуда
 ,(2.87)
,(2.87)
Сделав допущение, что
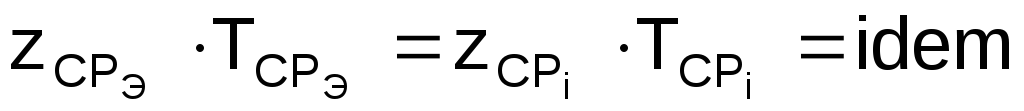 ,
и предположив, что режим течения
квадратичный, можно записать
,
и предположив, что режим течения
квадратичный, можно записать
 . (2.88)
. (2.88)
Выражая диаметр эквивалентного
газопровода через диаметр первого
участка, найдем эквивалентную длину
 .(2.89)
.(2.89)
Параллельные газопроводы
Рассмотрим сложный газопровод, состоящий
из нескольких параллельных ниток
различного диаметра (рис. 2.12).
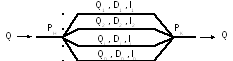
Рис.
2.12. Схема параллельных
газопроводов
Поскольку начальное и конечное давление
для каждой нитки параллельной системы
газопроводов одинаково, из уравнения
неразрывности следует, что
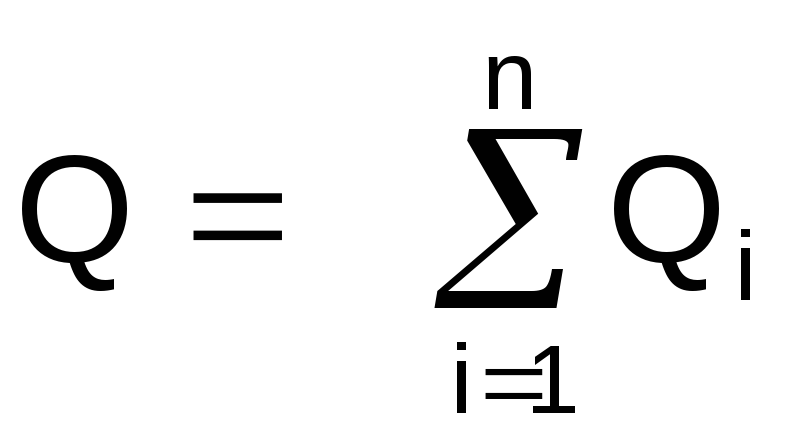 .(2.90)
.(2.90)
В этом случае для эквивалентного
газопровода будет справедливо соотношение
 .(2.91)
.(2.91)
Полагая, что режим течения квадратичный
и
 ,
из (2.90) получим
,
из (2.90) получим
 .(2.92)
.(2.92)
Эквивалентная длина параллельной
системы газопроводов составит
 .(2.93)
.(2.93)
Пользуясь уравнением расхода (2.84),
можно записать
 ,(2.94)
,(2.94)
откуда из условия квадратичного закона
сопротивления и выполнения
условия ,
расход в любой параллельной нитке
составит
,
расход в любой параллельной нитке
составит
 .(2.95)
.(2.95)
Если длины параллельных ниток одинаковы,
справедливо соотношение
 .(2.96)
.(2.96)
Нечваль А.М.
Проектирование нефтегазопроводов


 ассмотрим
однониточный газопровод с участками
различного диаметра (рис.2.11).
ассмотрим
однониточный газопровод с участками
различного диаметра (рис.2.11). .(2.84)
.(2.84) .(2.85)
.(2.85) ,(2.86)
,(2.86) .(2.89)
.(2.89)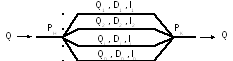
 .(2.91)
.(2.91) .(2.92)
.(2.92) .(2.93)
.(2.93) .(2.95)
.(2.95) .(2.96)
.(2.96)