Наименьший угол

Через каждую вершину треугольника Рёло, в отличие от остальных его граничных точек, проходит не одна опорная прямая, а бесконечное множество опорных прямых. Пересекаясь в вершине, они образуют «пучок». Угол между крайними прямыми этого «пучка» называется углом при вершине. Для фигур постоянной ширины угол при вершинах не может быть меньше 120°. Единственная фигура постоянной ширины, имеющая углы, равные в точности 120° — это треугольник Рёло.

Наименьшая центральная симметрия

Треугольник Рёло и его образ при центральной симметрии относительно своего центра. Наибольшая центрально-симметричная фигура, в нём содержащаяся, и наименьшая центрально-симметричная выпуклая, его содержащая выделены жирной линией

Из всех фигур постоянной ширины треугольник Рёло обладает центральной симметрией в наименьшей степени. Существует несколько различных способов дать определение степени симметричности фигуры. Один из них — это мера Ковнера — Безиковича. 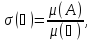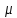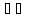В общем случае для выпуклой фигуры {\displaystyle C} она равна{\displaystyle \sigma (C)={{\mu (A)} \over {\mu (C)}},}где{\displaystyle \mu } — площадь фигуры, {\displaystyle A}A — содержащаяся в {\displaystyle C}  центрально-симметричная выпуклая фигура максимальной площади. Для треугольника Рёло такой фигурой является шестиугольник с искривлёнными сторонами, представляющий собой пересечение этого треугольника Рёло со своим образом при центральной симметрии относительно своего центра. Мера Ковнера — Безиковича для треугольника Рёло равна =0,84034.{\displaystyle \sigma ={{6\arccos {\left({{5+{\sqrt {33}}} \over {12}}\right)}+{\sqrt {3}}-{\sqrt {11}}} \over {\pi -{\sqrt {3}}}}=0{,}84034\ldots }Другой способ — это мера Эстерманна ,

{\displaystyle \tau (C)={{\mu (C)} \over {\mu (B)}},}где{\displaystyle B}B— содержащая{\displaystyle C}центрально-симметричная фигура минимальной площади. Для треугольника Рёло{\displaystyle B}B— этоправильный шестиугольник, поэтому мера Эстерманна равна=0,81379.

{\displaystyle \tau ={{\pi -{\sqrt {3}}} \over {\sqrt {3}}}=0{,}81379\ldots }Для центрально-симметричных фигур меры Ковнера — Безиковича и Эстерманна равны единице. Среди фигур постоянной ширины центральной симметрией обладает толькокруг, который (вместе с треугольником Рёло) и ограничивает область возможных значений их симметричности.

Качение по квадрату

Любая фигура постоянной ширины вписана в квадрат со стороной, равной ширине фигуры, причём направление сторон квадрата может быть выбрано произвольно. Треугольник Рёло — не исключение, он вписан в квадрат и может вращаться в нём, постоянно касаясь всех четырёх сторон.

Каждая вершина треугольника при его вращении «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах — там вершина описывает дугу эллипса. Центр этого эллипса расположен в противоположном углу квадрата ,а его  больша́я и малая оси повёрнуты на угол в 45° относительно сторон квадрата и равны,{\displaystyle a\cdot \left({\sqrt {3}}\pm 1\right),}где {\displaystyle a}a — ширина треугольника. Каждый из четырёх эллипсов касается двух смежных сторон квадрата на расстоянии{\displaystyle a\cdot \left(1-{{\sqrt {3}} \over {2}}\right)=a\cdot 0{,}13397\ldots }от угла.

Центр треугольника Рёло при вращении движется по траектории, составленной из четырёх одинаковых дуг эллипсов. Центры этих эллипсов расположены в вершинах квадрата, а оси повёрнуты на угол в 45° относительно сторон квадрата и равны .

{\displaystyle a\cdot \left(1\pm {{1} \over {\sqrt {3}}}\right)}Иногда для механизмов, реализующих на практике такое вращение треугольника, в качестве траектории центра выбирают не склейку из четырёх дуг эллипсов, а близкую к ней окружность.

Площадь каждого из четырёх не затронутых вращением уголков равна и, вычитая их из площади квадрата, можно получить площадь фигуры, которую образует треугольник Рёло при вращении в нём{\displaystyle a^{2}-4\beta =a^{2}\cdot \left(2{\sqrt {3}}+{{\pi } \over {6}}-3\right)=a^{2}\cdot 0{,}98770\ldots }азница с площадью квадрата составляет ≈1,2 %, поэтому на основе треугольника Рёло создают свёрла, позволяющие получать почти квадратные отверстия.