
- •Моделирование, идентификация и компьютерная имитация объекта управления
- •Маятник как объект управления
- •Математическая модель оу
- •Компьютерная модель (имитационная модель)
- •Учёт сопротивления воздуха
- •Учёт трения в точке подвеса
- •Выбор алгоритма стабилизации маятника
- •Временные и частотные характеристики элементов и систем управления
- •Временные характеристики (вх)
- •Частотные характеристики (чх)
- •Устойчивость объектов и систем управления
- •Синтез систем управления.
- •Операторный метод.
- •Дискретная система управления.
- •6.1 Выплата кредита.
- •6.2 Генератор чисел Фибоначчи.
- •6.3. Генератор псевдослучайных последовательностей.
- •6.4. Фильтр ма(3)
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра АПУ
Отчеты по лабораторным работам
по дисциплине «Теория управления»
|
Студенты гр. 5371 |
|
Уруков С.Д. |
|
|
|
Шадзевская А. |
|
Преподаватель |
|
Профессор Имаев Д.Х. |
Санкт-Петербург
2018
-
Моделирование, идентификация и компьютерная имитация объекта управления
-
Маятник как объект управления
На рис. 1.1 изображена принципиальная схема маятника, где m – сосредоточенная масса (кг), l – длина маятника; g = 9.81 (м/с2) – ускорение свободного падения; y(t) – угол отклонения маятника. Примем следующие допущения:
-
Отсутствует трение;
-
Нет сопротивления воздуха.

Рис. 1.1
-
Математическая модель оу
Составим уравнение баланса моментов, действующих на маятник: момент силы тяжести, момент за счёт движения с ускорением (II закон Ньютона). Уравнения баланса выглядят так:


Получено нелинейное дифференциальное уравнение второго порядка. Это уравнение однородное (без правой части), что означает отсутствие внешних воздействий, как управляющих, так и возмущающих (объект автономный). Если поделить уравнение (1.1) на ml2, то уравнение упрощается:
 .
(1.2)
.
(1.2)
Линейное уравнение решается аналитически:

где
 —
круговая частота колебаний (
—
круговая частота колебаний (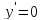 ).
).
Круговая частота
колебаний
 связана с периодом
связана с периодом следующим соотношением:
следующим соотношением:
 .
.
Отсюда получим формулу:

Если
 («секундный маятник»), то длина маятника
(«секундный маятник»), то длина маятника
 равняется:
равняется:

-
Компьютерная модель (имитационная модель)
Выберем программную среду для научно-технических расчётов Matlab/Simulink фирмы The MathWorks, Inc.
Реализация математической модели на языке графического редактора Simulink упрощается, если дифференциальное уравнение разрешить относительно старшей производной.
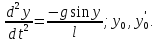 (1.2)
(1.2)
На рис. 1.2 представлена компьютерная модель маятника на языке графического редактора Simulink.

Рис.1.2.
На рис. 1.3 представлен
результат компьютерной имитации при
начальных условиях
 .
.

Рис. 1.3.
-
Учёт сопротивления воздуха
Колебания реального маятника со временем затухают, что объясняется потерей энергии на преодоление сопротивления воздуха. Примем гипотезу о том, что момент сопротивления пропорционален угловой скорости. Уравнение баланса моментов примет вид:


где
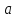 – неизвестный коэффициент пропорциональности.
– неизвестный коэффициент пропорциональности.
Оценка неизвестного параметра a проводилась экспериментальным способом: установим число колебаний секундного маятника, за которое амплитуда колебания уменьшиться в половину раз. По истечении 10 периодов колебаний амплитуда уменьшается в половину.
Отредактируем компьютерную модель (рис. 1.2) с учетом момента сопротивления, то есть в соответствии с дифференциальным уравнением (1.3)

-
Учёт трения в точке подвеса
Колебания реального маятника со временем затухают полностью, что объясняется наличием кулоновского трения в точке подвеса. Момент трения постоянен по величине и направлен против движения, что моделируется так:

Компьютерная модель представлена на рис. 1.4.

Рис. 1.4.
Эксперимент с реальным маятником показал, что примерно за 25 секунд маятник останавливается.
Вывод: как показывают результаты компьютерного моделирования (рис. 1.5) математическая модель адекватна реальному секундному маятнику.

Рис. 1.5.
