14. Импульс. Закон сохранения импульса.

Импульс тела (или количество движения) − это векторная физическая величина, равная произведению массы тела на его скорость.

Единица измерения импульса в СИ – кг*м/с

Закон сохранения импульса: если сумма внешних сил, действующих на точки системы, равна нулю, то сумма импульсов всех точек системы остается величиной постоянной.

15. Энергия. Кинетическая и потенциальная энергия. Теорема об изменении кинетической энергии. Закон сохранения энергии в механики.

Работа − это количественная характеристика процесса обмена энергией между взаимодействующими телами.

Кинетическая энергия − это энергия тела, обусловленная его механическим движением

Теорема об изменении кинетической энергии:

Потенциальная энергия − часть общей механической энергии системы, зависящей от взаимного расположения материальных точек системы и их положения во внешнем силовом поле.

К₁ + П₁ = К₂ + П₂ = const (1)

Величину E = К + П называют полной механической энергией системы.

Из соотношения (1) следует закон сохранения полной механической энергии: полная механическая энергия системы, на материальные точки которой действуют только консервативные силы, с течением времени не изменяется:

E = const.

16. Момент импульса материальной точки относительно некоторого центра. Чему равен модуль вектора момента импульса? Что называется плечом импульса? Момент импульса в си.

Момент импульса − векторная величина, равная векторному произведению радиус-вектора 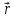точки, проведенного из центра на ее импульс .

Модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению им-пульса p на плечо импульса d относительно этой оси.

Модуль вектора момента импульса равен:

где d − плечо импульса относительно точки О.

Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

17. Как определяется направление вектора момента импульса.

Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу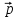, и он перпендикулярен как вектор , так и вектору.

18. Момент силы материальной точки относительно некоторого центра.

Момент силы - векторная величина, равная векторному произведению радиус-вектора точки, проведенному из полюса в точку приложения силы, на силу:

19. Формула для определения модуля вектора момента силы. Плечо силы. Момент силы в СИ.

Модуль вектора момента силы равен:

где d = r sin α − плечо силы относительно точки О.

Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.

Момент силы измеряется в ньютон-метрах. 1 Н·м

20. Как определяется направление вектора момента силы.

Направление момента силы совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора 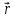к силе, и он перпендикулярен как вектору, так и вектору

21. Момент инерции тела относительно данной оси. Физический смысл момента инерции. Момент инерции в СИ

Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:

^[I] = 1 кг · м²

Физический смысл момента инерции можно определить из выражения:

Момент инерции тела является мерой инерции тела при вращательном движении.

22. Теорема Штейнера. Правило аддитивности для момента инерции.

Теорема Штейнера: момент инерции тела I_z относительно произвольной оси равен сумме момента инерции I_c относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:

Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:

23. Формула для расчета работы силы при вращении тела.

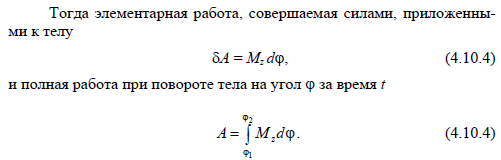
24. Основное уравнение динамики вращательного движения относительно точки. Закон сохранения момента импульса.

Уравнение динамики вращательного движения относительно точки (или иначе закон изменения момента импульса механической системы)

Производная по времени от момента импульса системы относительно точки равна сумме моментов внешних сил относительно этой точки.

Закон сохранения момента импульса: если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы остаётся величиной постоянной.

25. Основное уравнение динамики вращательного движения относительно неподвижной оси. Закон сохранения проекции момента импульса.

Основное уравнение динамики вращательного движения относительно неподвижной оси:

Закон сохранения проекции момента импульса:

Если проекцию моментов внешних сил относительно оси z равна нулю, то момент импульса тела относительно этой оси остаётся величиной постоянной.

26. Кинетическая энергия тела вращающегося вокруг неподвижной оси. Кинетическая энергия тела при плоском движении.

27. Свободные гармонические колебания и их характеристики( смещение, амплитуда, частота и период колебаний, циклическая частота фаз и начальная фаза колебаний).

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени.

Периодические колебания − значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени.

Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид:

28. Дать определение частоты обращения тела. Дайте определение периода обращения тела.

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения - это время, за которое совершается один оборот. Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения.

29.Характеристики колебательной системы. Коэффициент затухания и логарифмический декремент затухания. Время релаксации. Добротность колебательной системы.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать.

30. Уравнение состояния идеального газа(Клапейрона – Менделеева).

Уравнением состояния идеального газа или уравнение Менделеева − Клапейрона.

31. Внутренняя энергия идеального газа. Дать определение числа степеней свободы молекулы газа. Работа газа при изменении его объёма.

Число степеней свободы − это число независимых координат (переменных), которые полностью определяют положение системы в пространстве.

Молекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения. Молекула двухатомного газа рассматривается как совокупность двух материальных точек,

связанных недеформированной связью. Эта система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Трехатомная молекула имеет шесть степеней свободы: три поступательные и три вращательные. Столько же степеней свободы будут иметь и многоатомные молекулы (четырех, пяти и т. д.).