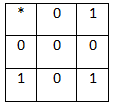
6. Операция вычитания в 2-й сс.

Правила вычитания в 2-й СС.

-	0	1
0	0	1
1	1*	0

Звездочкой отмечен случай, когда в текущем разряде получена единица, путем займа из ближайшего старшего разряда.

Пример.

_ 1000111001

0101101101

0011001100

В ЭВМ никогда в перечне выполняемых операций арифметического устройства не присутствует одновременно операция сложения и операция вычитания. При этом, как правило, присутствует только операции сложения. Что же касается операции вычитания, то она реализуется за счет прибавления к уменьшаемому значения вычитаемого, взятого с противоположным знаком.

7. Операция умножения в 2-й сс начиная со старшего разряда множителя со сдвигом множимого.

При умножении многоразрядных операндов, как правило (особенно в десятичной системе счисления), используется метод, при котором формирование произведения выполняется за счет суммирования частичных произведений, которые оформляются посредством умножения множимого на отдельные разряды множителя с учетом веса соответствующего разряда множителя. При последовательном способе формирования частичных произведений последние могут рассчитываться поочередно для отдельных разрядов множителя начиная с младшего или старшего разряда. При десятичном основании, как правило, формирование частичных произведений осуществляется начиная с младшего разряда множителя.

---------------------------------------------------------------------------------------------------------------

8. Операция умножения в 2-й сс начиная с младшего разряда множителя со сдвигом множимого.

При последовательном способе формирования частичных произведений последние могут рассчитываться поочередно для отдельных разрядов множителя начиная с младшего или старшего разряда. При десятичном основании, как правило, формирование частичных произведений осуществляется начиная с младшего разряда множителя.

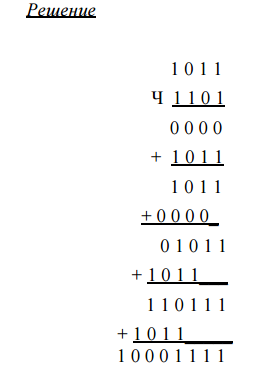
Реализация данного метода умножения требует использовать 2n-разрядный сумматор для последовательного, от такта к такту, формирования 2n-разрядного произведения и 2n-разрядный регистр для хранения и сдвига влево множимого. В данном примере для того, чтобы учесть то, что очередной разряд множителя имеет вес, в два раза больший, чем предыдущий разряд, его частичное произведение учитывается со сдвигом множимого на один разряд влево при суммировании с промежуточным результатом. В таком случае говорят, что умножение выполняется со сдвигом множимого.

---------------------------------------------------------------------------------------------------------------

Возможные методы реализации операции умножения можно классифицировать по двум признакам:

– Начиная с какого разряда (со старшего или младшего) выполняется отработка множителя;

– Что сдвигается – множимое или промежуточное произведение.

Используя эти два классификационных признака, можно выделить четыре метода умножения:

– Умножение с младших разрядов множителя со сдвигом множимого; при реализации данного метода требуется 2n- разрядный сумматор, 2n- разрядный регистр промежуточного произведения, 2n - разрядный регистр для хранения и сдвига множимого и n- разрядный регистр для хранения множителя;

– Умножение с младших разрядов множителя со сдвигом промежуточного произведения; при реализации данного метода требуется n-разрядный сумматор, 2n-разрядный регистр промежуточного произведения, n-разрядный регистр для хранения множимого и n-разрядный регистр для хранения множителя;

– Умножение со старшего разряда множителя со сдвигом множимого; при реализации данного метода требуется 2n-разрядный сумматор, 2n-разрядный регистр промежуточного произведения, 2n- разрядный регистр для хранения и сдвига множимого и n-разрядный регистр для хранения множителя;

– Умножение со старшего разряда множителя со сдвигом промежуточного произведения; при реализации данного метода требуется n-разрядный сумматор, 2n-разрядный регистр промежуточного произведения, n-разрядный регистр для хранения множимого и n-разрядный регистр для хранения множителя.