
- •Алгоритмы,
- •НАЗНАЧЕНИЯ АЛГОРИТМОВ
- •НЕРАЗМЫШЛЯЮЩИЙ
- •АЛГОРИТМЫ
- •Виды алгоритмов
- •СВОЙСТВА АЛГОРИТМОВ
- •СВОЙСТВА АЛГОРИТМА
- •СВОЙСТВА
- •СВОЙСТВА
- •КРИТЕРИИ СРАВНЕНИЯ АЛГОРИТМОВ
- •КРИТЕРИИ СРАВНЕНИЯ АЛГОРИТМОВ
- •Начал
- •РАЗРАБОТКА
- •ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ СТРУКТУРЫ АЛГОРИТМА
- •БЛОК-СХЕМА
- •БАЗОВЫЕ КОНСТРУКЦИИ АЛГОРИТМА
- •АЛГОРИТМИЧЕСКИЕ
- •АЛГОРИТМИЧЕСКИЕ
- •АЛГОРИТМИЧЕСКИЕ
- •АЛГОРИТМИЧЕСКИЕ
- •ПРИМЕР
- •Истина
- •БАЗОВЫЕ АЛГОРИТМЫ
- •БАЗОВЫЕ АЛГОРИТМЫ
- •БАЗОВЫЕ АЛГОРИТМЫ
- •Пример.
- •БАЗОВЫЕ АЛГОРИТМЫ
- •Пример. Вычислить сумму N первых натуральных чисел. Использовать цикл с предусловием.
- •Пример.
- •ТРЕНИН
- •ТРЕНИН
- •Пример.
- •ТРЕНИНГ
- •ПРИМЕ Р 7
- •ТРЕНИНГ
- •ВСПОМОГАТЕЛЬНЫЕ
- •ВСПОМОГАТЕЛЬНЫЕ
- •ВСПОМОГАТЕЛЬНЫЕ
- •1. Могилев А.В. Информатика / А. В. Могилев, Н. И. Пак, Е. К.
- •ОСНОВЫ АЛГЕБРЫ ЛОГИКИ
- •ОСНОВЫ АЛГЕБРЫ ЛОГИКИ
- •Формы
- •Формы
- •Формы
- •Формы
- •Алгебра высказываний служит для определения истинности или ложности составных высказываний, не вникая в
- •СОСТАВНОЕ ВЫСКАЗЫВАНИЕ содержит высказывания, объединенные логическими операциями.
- •Логическое умножение (конъюнкция) -
- •Пример 1.
- •Логическое сложение (дизъюнкция)-
- •Логическое отрицание (инверсия) –
- •Импликация двух высказываний A и B - такое высказывание, которое ложно тогда и
- •Эквиваленция двух высказываний A и B - такое высказывание, которое истинно тогда и
- •Логической переменной называется переменная, значением которой может быть любое высказывание, например: x, у,
- •Формулы А и B, зависящие от одного и того же набора переменных x1,
- •ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
- •ЛОГИЧЕСКИЕ ФУНКЦИИ
- •ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ
- •БУЛЕВЫ ФУНКЦИИ ДВУХ АРГУМЕНТОВ
- •Инверсия
- •Основные законы и тождества булевой
- •Любой из основных законов и тождеств булевой алгебры может быть доказан с помощью
- •Законы алгебры логики можно доказать
- •Законы алгебры логики можно доказать путем тождественных преобразований.
- •Формула А называется тавтологией (или тождественно истинной),
- •Формула А называется тождественно ложной,
- •Пример 11. Определить x, если:
- •Пример 12.
- •Пример 13.
- •Любую формулу можно преобразовать к равносильной ей, в которой используются только операции НЕ,
- •Пример 15.
- •Пример 16.
- •Решение логических задач
- •Пример 17.
- •На вопрос «Кто из трех студентов изучал
- •Пример 18.
- •Таблица истинности для F1
- •Таблицы истинности. Обучающая программа «Logic»
- •БАЗОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ ЭВМ
- •Логические элементы компьютера
- •КОНЪЮНКТОР
- •ДИЗЪЮНКТОР
- •ИНВЕРТОР
- •ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- •КАНОНИЧЕСКИЕ ФОРМЫ БУЛЕВЫХ
- •КАНОНИЧЕСКИЕ ФОРМЫ БУЛЕВЫХ ФУНКЦИЙ
- •СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (СДНФ) логической функции
- •ПОЛУЧЕНИЕ СДНФ ФУНКЦИИ С ПОМОЩЬЮ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- •ПЕРЕХОД ОТ ТАБЛИЦЫ ИСТИННОСТИ ФУНКЦИИ К СДНФ
- •ПЕРЕХОД ОТ ТАБЛИЦЫ ИСТИННОСТИ ФУНКЦИИ К СДНФ
- •ПЕРЕХОД ОТ ТАБЛИЦЫ ИСТИННОСТИ
- •Построить логическую схему функции:
- •ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ ФУНКЦИИ
- •ТАБЛИЦА ИСТИННОСТИ
- •ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ ФУНКЦИИ
- •РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ. ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ ФУНКЦИИ
- •РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ. ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ ФУНКЦИИ
- •РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ. ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ
- •ДВОЙСТВЕННОСТЬ ЛОГИЧЕСКИХ ОПЕРАЦИЙ: ДИЗЪЮНКЦИИ И КОНЪЮНКЦИИ
- •Элементарной дизъюнкцией называется дизъюнкция нескольких переменных и/или их инверсий.
- •Совершенной конъюнктивной нормальной формой (СКНФ ) функции
- •СКНФ функции F (x1, x2, … , xn) можно получить:
- •Построение СКНФ функции по таблице истинности:
- •ПРАВИЛО ПОЛУЧЕНИЯ СКНФ ФУНКЦИИ F С ПОМОЩЬЮ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ

ЛОГИЧЕСКИЕ ФУНКЦИИ
Любое составное высказывание можно рассматривать как логическую функцию
F(X1, X2, …, XN), аргументами которой являются логические переменные X1, X2, …, XN - простые высказывания.
Функция и аргументы могут принимать только два различных значения: «истина» (1) и «ложь» (0).
63

ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ
Таблица истинности определяет истинность или ложность высказывания (логического выражения) при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
Количество строк в таблице истинности логического выражения определяется количеством логических переменных (N), равно 2 N.
Логические выражения, у которых таблицы истинности совпадают, называются
равносильными или эквивалентными.
64
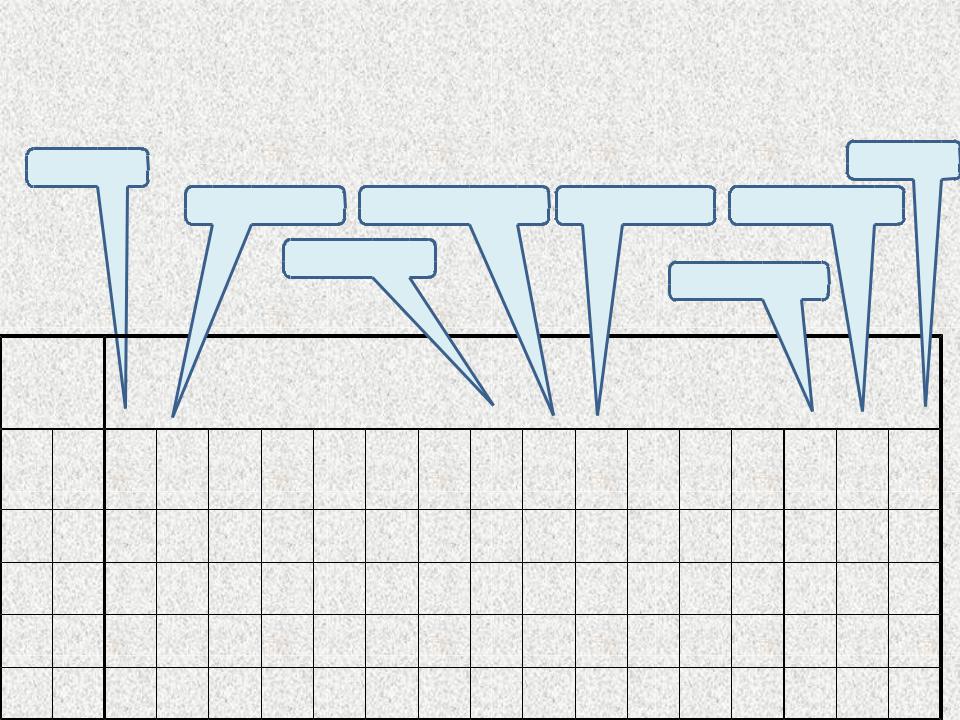
БУЛЕВЫ ФУНКЦИИ ДВУХ АРГУМЕНТОВ
Количество строк в таблице: N1=22 = 4. |
|||
Число различных F(A,B) - число столбцов в |
|||
F(A,B) |
=24 = 16. |
|
|
N =2N1 |
F(A,B)= (A |
F(A,B)=A |
|
=02 |
F(A,B)=А |
||
|
&B |
V B) |
B |
V
Аргу- мент
ы
таблице:F(A,B)
F(A,B)= (=1
A&B)
А В F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 F11 F12 F13 F14 F15 F16 |
||||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|

Инверсия |
дизъюнкции |
(«стрелка |
||
Пирса», «ИЛИ-НЕ»): F(A,B)= A B = (A |
||||
V B) |
А |
В |
F(A,B)= A B = (A V |
|
|
|
|
B) |
|
|
0 |
0 |
1 |
|
|
0 |
1 |
0 |
|
|
1 |
0 |
0 |
|
|
1 |
1 |
0 |
(«штрих |
Инверсия |
|
конъюнкции |
||
Шеффера», «И-НЕ»): F(A,B)= A B = (A |
||||
& B) |
А |
В |
F(A,B)= A B = (A & |
|
|
|
|
B) |
|
|
0 |
0 |
1 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
1 |
66 |
|
1 |
1 |
0 |
|
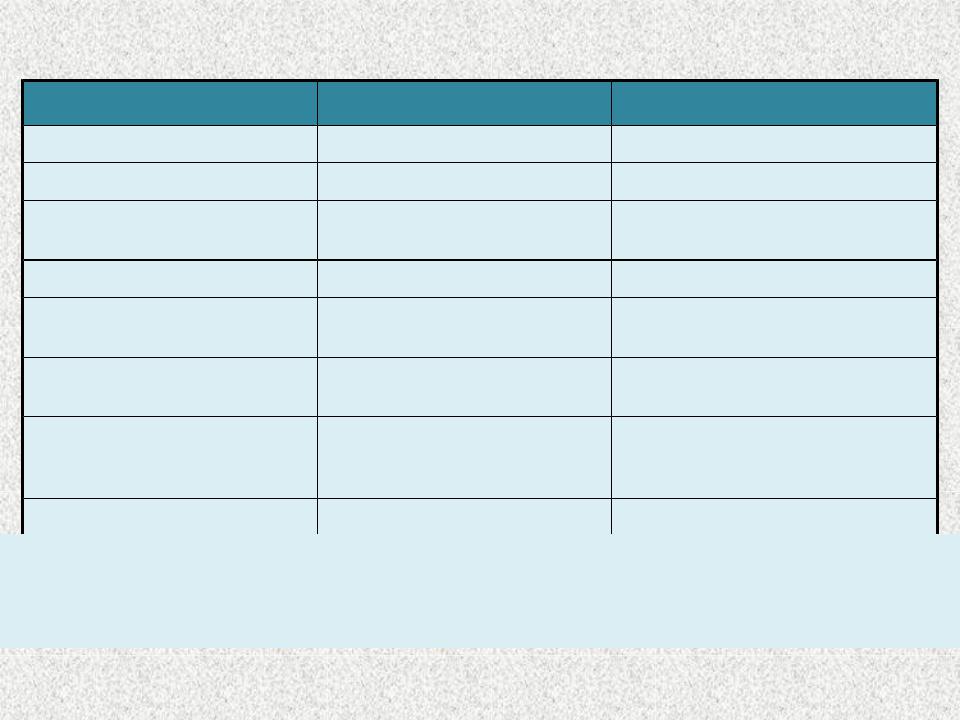
Основные законы и тождества булевой
|
алгебры |
Для конъюнкции |
|
Для дизъюнкции |
|
Ассоциативность |
АV(ВVС)=(АVВ)VС |
А&(В&С)=(А&В)&С |
Коммутативность |
А VВ=ВVА |
А&В=В&А |
Дистрибутивность |
А&(ВVС)=(А&B)V(A |
АV(В&С)=(АVВ)&(АVС |
|
&C) |
) |
Идемпотентность |
АVА=А |
А&А=А |
Операции с |
АV1=1 |
А&1=А |
константами |
АV0=А |
А&0=0 |
Правила де |
(АVВ)= А & В |
(А&В)= А V В |
Моргана |
|
|
Операции |
АVĀ=1 |
А&Ā=0 |
переменной с её |
|
|
инверсией |
|
|
Правила |
АV(А&В)=А |
А&(АVВ)=А |
Правило замены операции импликации: A B = A V B
Правило замены операции эквивалентности: A B = ( A V B) V (A Правило двойной инверсии: А =А
67
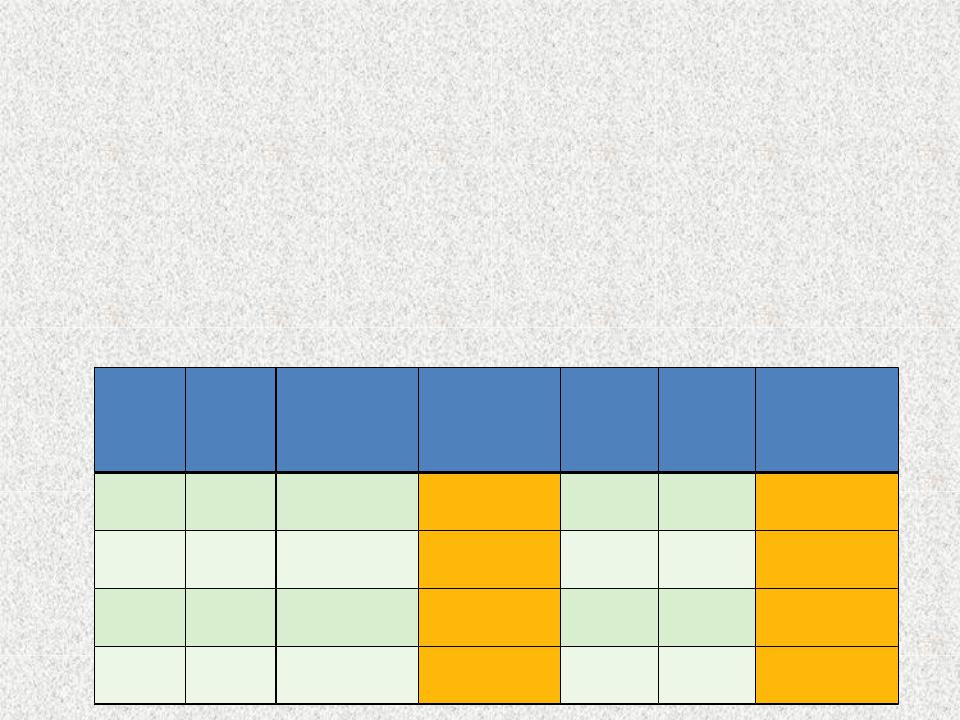
Любой из основных законов и тождеств булевой алгебры может быть доказан с помощью таблиц истинности.
Пример 6.
Правило де Моргана: (x & у) = x V y
x y x & у |
(x & x |
y |
x V |
|
|||
|
|
|
у) |
|
|
y |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
68 |

Законы алгебры логики можно доказать
путем логических рассуждений.
Пример 7. Доказательство первого закона поглощения:
x V (x & у )= x
• Пусть истинна правая часть, т. е. x = 1, тогда в
левой части дизъюнкция x v (x & у) истинна.
• Пусть истинна левая часть.
Тогда по определению дизъюнкции истинна или формула x, или формула (x & у), или обе эти формулы одновременно.
• Если x ложна, тогда (x & у) ложна,
следовательно, x может быть только истинной.
69

Законы алгебры логики можно доказать путем тождественных преобразований.
Пример 8.
Доказательство первого закона поглощения x v (x & у )= x
x V (x & у ) = (x & 1 ) V (x & у ) = x & (1 V y) = x
70

Формула А называется тавтологией (или тождественно истинной),
если она истинна при любых значениях своих переменных.
Пример 9.
х V х =1
(операция переменной с её инверсией)
71

Формула А называется тождественно ложной,
если она равна 0 при любых значениях своих переменных.
Пример 10.
х & х =0
72
