
- •Алгоритмы,
- •НАЗНАЧЕНИЯ АЛГОРИТМОВ
- •НЕРАЗМЫШЛЯЮЩИЙ
- •АЛГОРИТМЫ
- •Виды алгоритмов
- •СВОЙСТВА АЛГОРИТМОВ
- •СВОЙСТВА АЛГОРИТМА
- •СВОЙСТВА
- •СВОЙСТВА
- •КРИТЕРИИ СРАВНЕНИЯ АЛГОРИТМОВ
- •КРИТЕРИИ СРАВНЕНИЯ АЛГОРИТМОВ
- •Начал
- •РАЗРАБОТКА
- •ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ СТРУКТУРЫ АЛГОРИТМА
- •БЛОК-СХЕМА
- •БАЗОВЫЕ КОНСТРУКЦИИ АЛГОРИТМА
- •АЛГОРИТМИЧЕСКИЕ
- •АЛГОРИТМИЧЕСКИЕ
- •АЛГОРИТМИЧЕСКИЕ
- •АЛГОРИТМИЧЕСКИЕ
- •ПРИМЕР
- •Истина
- •БАЗОВЫЕ АЛГОРИТМЫ
- •БАЗОВЫЕ АЛГОРИТМЫ
- •БАЗОВЫЕ АЛГОРИТМЫ
- •Пример.
- •БАЗОВЫЕ АЛГОРИТМЫ
- •Пример. Вычислить сумму N первых натуральных чисел. Использовать цикл с предусловием.
- •Пример.
- •ТРЕНИН
- •ТРЕНИН
- •Пример.
- •ТРЕНИНГ
- •ПРИМЕ Р 7
- •ТРЕНИНГ
- •ВСПОМОГАТЕЛЬНЫЕ
- •ВСПОМОГАТЕЛЬНЫЕ
- •ВСПОМОГАТЕЛЬНЫЕ
- •1. Могилев А.В. Информатика / А. В. Могилев, Н. И. Пак, Е. К.
- •ОСНОВЫ АЛГЕБРЫ ЛОГИКИ
- •ОСНОВЫ АЛГЕБРЫ ЛОГИКИ
- •Формы
- •Формы
- •Формы
- •Формы
- •Алгебра высказываний служит для определения истинности или ложности составных высказываний, не вникая в
- •СОСТАВНОЕ ВЫСКАЗЫВАНИЕ содержит высказывания, объединенные логическими операциями.
- •Логическое умножение (конъюнкция) -
- •Пример 1.
- •Логическое сложение (дизъюнкция)-
- •Логическое отрицание (инверсия) –
- •Импликация двух высказываний A и B - такое высказывание, которое ложно тогда и
- •Эквиваленция двух высказываний A и B - такое высказывание, которое истинно тогда и
- •Логической переменной называется переменная, значением которой может быть любое высказывание, например: x, у,
- •Формулы А и B, зависящие от одного и того же набора переменных x1,
- •ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
- •ЛОГИЧЕСКИЕ ФУНКЦИИ
- •ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ
- •БУЛЕВЫ ФУНКЦИИ ДВУХ АРГУМЕНТОВ
- •Инверсия
- •Основные законы и тождества булевой
- •Любой из основных законов и тождеств булевой алгебры может быть доказан с помощью
- •Законы алгебры логики можно доказать
- •Законы алгебры логики можно доказать путем тождественных преобразований.
- •Формула А называется тавтологией (или тождественно истинной),
- •Формула А называется тождественно ложной,
- •Пример 11. Определить x, если:
- •Пример 12.
- •Пример 13.
- •Любую формулу можно преобразовать к равносильной ей, в которой используются только операции НЕ,
- •Пример 15.
- •Пример 16.
- •Решение логических задач
- •Пример 17.
- •На вопрос «Кто из трех студентов изучал
- •Пример 18.
- •Таблица истинности для F1
- •Таблицы истинности. Обучающая программа «Logic»
- •БАЗОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ ЭВМ
- •Логические элементы компьютера
- •КОНЪЮНКТОР
- •ДИЗЪЮНКТОР
- •ИНВЕРТОР
- •ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- •КАНОНИЧЕСКИЕ ФОРМЫ БУЛЕВЫХ
- •КАНОНИЧЕСКИЕ ФОРМЫ БУЛЕВЫХ ФУНКЦИЙ
- •СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (СДНФ) логической функции
- •ПОЛУЧЕНИЕ СДНФ ФУНКЦИИ С ПОМОЩЬЮ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- •ПЕРЕХОД ОТ ТАБЛИЦЫ ИСТИННОСТИ ФУНКЦИИ К СДНФ
- •ПЕРЕХОД ОТ ТАБЛИЦЫ ИСТИННОСТИ ФУНКЦИИ К СДНФ
- •ПЕРЕХОД ОТ ТАБЛИЦЫ ИСТИННОСТИ
- •Построить логическую схему функции:
- •ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ ФУНКЦИИ
- •ТАБЛИЦА ИСТИННОСТИ
- •ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ ФУНКЦИИ
- •РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ. ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ ФУНКЦИИ
- •РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ. ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ ФУНКЦИИ
- •РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ. ПЕРЕХОД ОТ ЛОГИЧЕСКОЙ СХЕМЫ К ФОРМУЛЕ
- •ДВОЙСТВЕННОСТЬ ЛОГИЧЕСКИХ ОПЕРАЦИЙ: ДИЗЪЮНКЦИИ И КОНЪЮНКЦИИ
- •Элементарной дизъюнкцией называется дизъюнкция нескольких переменных и/или их инверсий.
- •Совершенной конъюнктивной нормальной формой (СКНФ ) функции
- •СКНФ функции F (x1, x2, … , xn) можно получить:
- •Построение СКНФ функции по таблице истинности:
- •ПРАВИЛО ПОЛУЧЕНИЯ СКНФ ФУНКЦИИ F С ПОМОЩЬЮ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ
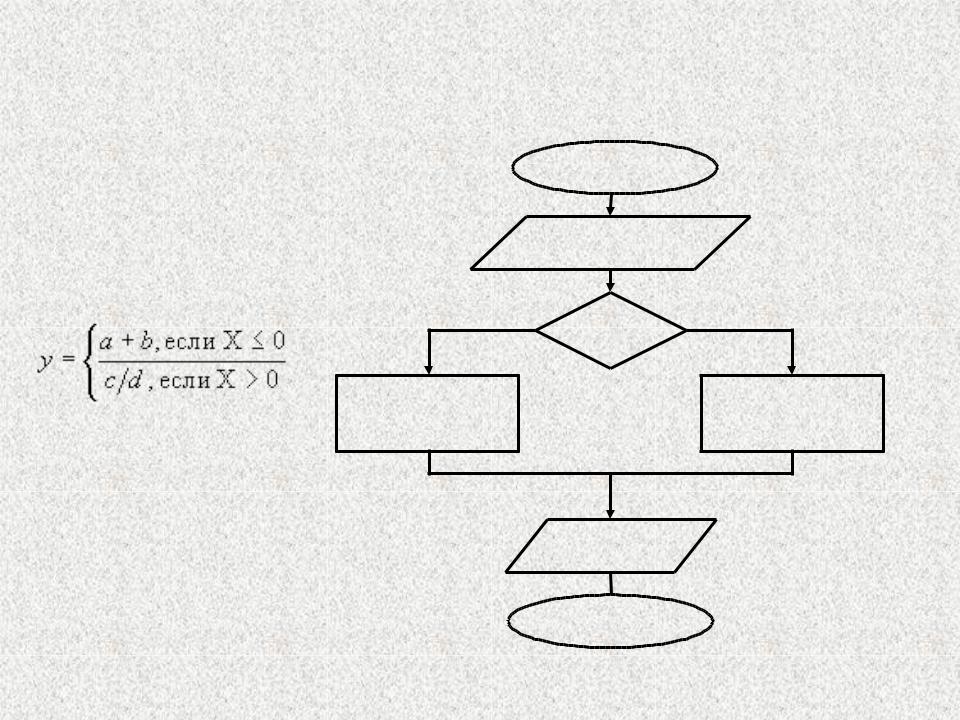
ПРИМЕР
оритм вычисления функции:
да
начало
Ввод a, b, c, d,
x
нет
X >
0
Y = c / d |
Y = a + b |
Вывод Y
конец
Истина
Ложь Услов ие
от, до Ложь Услов Истина шаг
ие
|
|
|
|
|
|
|
|
Д1 |
||
|
|
|
|
Д1 |
||||||
Д1 |
|
|
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
http://inf1.info

БАЗОВЫЕ АЛГОРИТМЫ
Алгоритм поиска наибольшего (наименьшего) значения:
За max (min) принимаем значение любого из входных данных и поочередно их сравниваем.
Если окажется, что очередное значение входного данного больше (меньше) max (min) , то max (min) присваиваем это значение.
Алгоритм использует неполное ветвление.
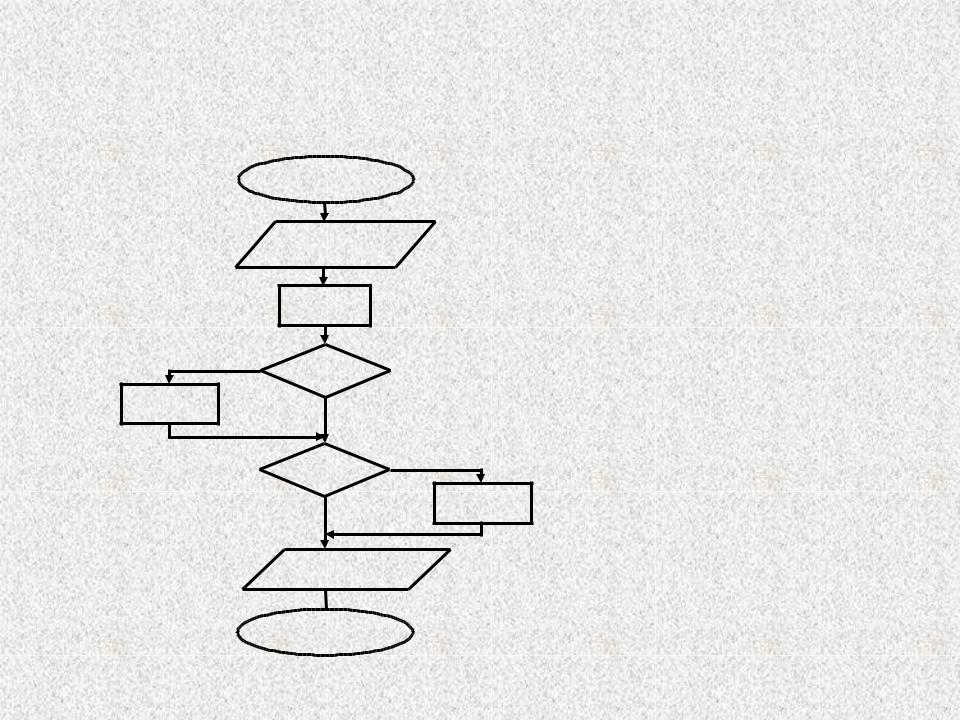
БАЗОВЫЕ АЛГОРИТМЫ
Пример: |
начало |
a=9 b=3 |
|
c=5 |
|
|
|
min=9 |
|
Ввод a, b, c |
3<9 |
|
min |
min=3 |
|
5<3 |
|
д |
=a |
|
b<mi |
|
|
а |
|
|
min= |
nнет |
|
b |
c<m |
д |
|
||
|
а |
|
|
in |
min= |
|
нет |
c |
|
Вывод min |
|
|
Ответ: запись в |
|
|
конец |
|
|
переменную min |
|
|
|
наименьшего из трех |
|
|
чисел: |

БАЗОВЫЕ АЛГОРИТМЫ
Правило произведения:
•начальное значение произведения Р=1;
•в теле некоторой циклической конструкции выполнить команду: Р = Р * <множитель>
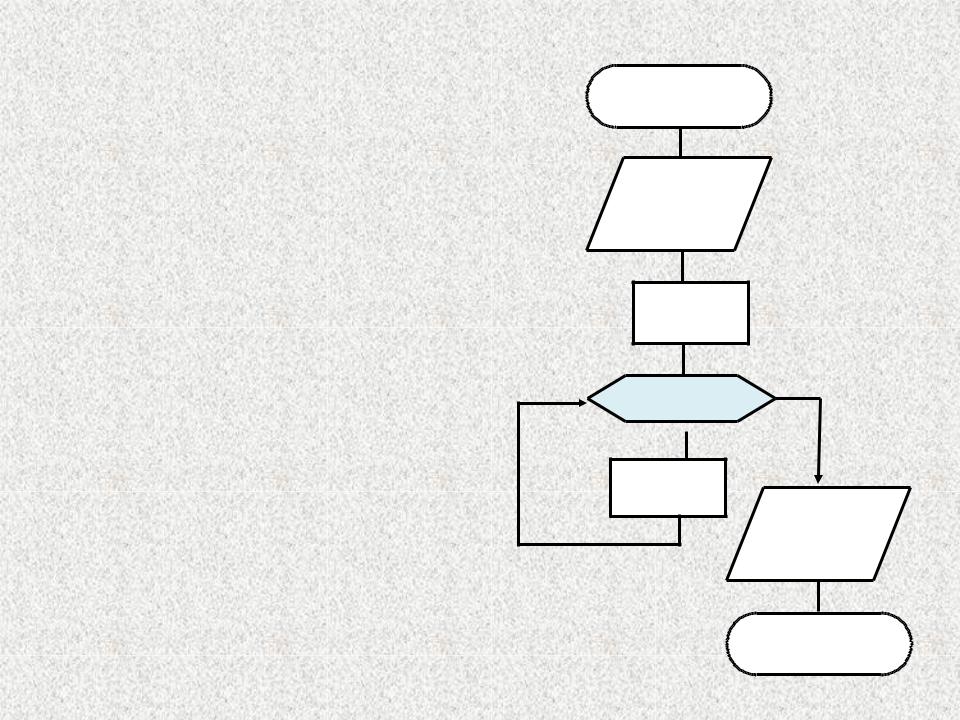
Пример.
Алгоритм вычислить факториала (F) натурального числа N: F=N!=1 2 3… N.
Используется цикл со счетчиком (i).
N=4
F=1
i=1
i=2F=1*1=1 F=1*2=2i=3 F=2*3i=4 =6*4=24
Начало
Ввод N
F=1
i = 1, N, 1
F=F*i
Вывод F
Конец

БАЗОВЫЕ АЛГОРИТМЫ
Правило суммирования:
•начальное значение суммы S=0;
•в теле некоторой циклической конструкции выполнить команду: S = S + <слагаемое>
Правило счетчика:
начальное значение счетчика K=0;в теле некоторой циклической
конструкции выполнить команду: K = K + 1
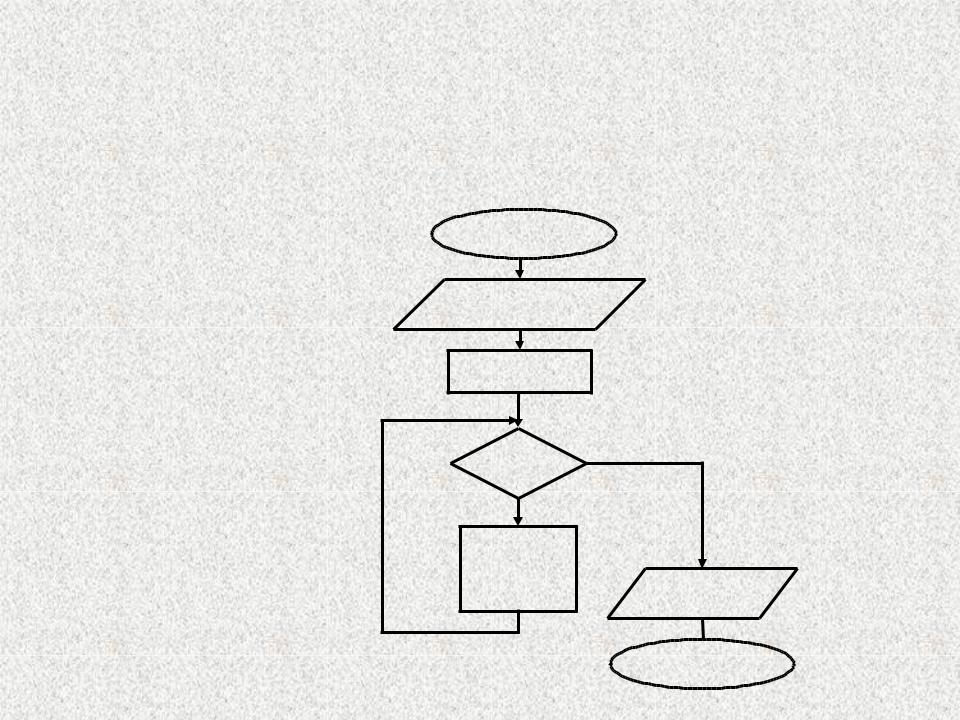
Пример. Вычислить сумму N первых натуральных чисел. Использовать цикл с предусловием.
N=5
S=0 i=1
S=0+1=1 i=2S=1+2=3 i=3S=3+3=6 i=4S=6+4=10
i=5S=10+5=15 i=6
S=15
начало
Ввод N
S=0, i=1
i > |
да |
|
|
N нет |
|
S=S+i |
|
i=i+1 |
Вывод S |
|
|
|
конец |
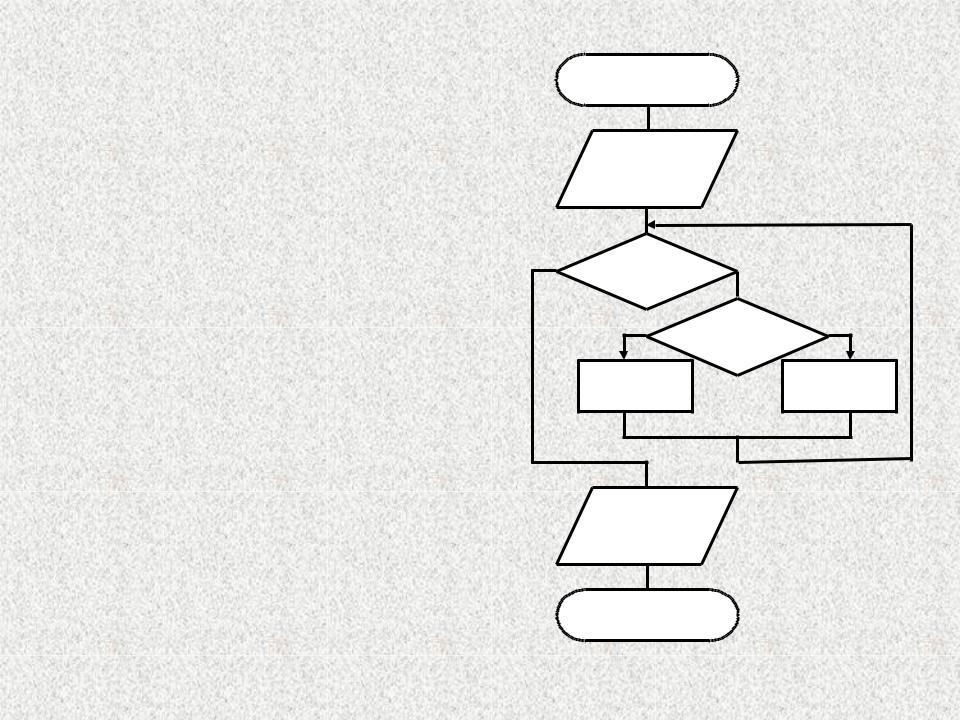
Пример.
Алгоритм Евклида –
определение НОД (наибольшего общего делителя) двух натуральных чисел m и n (m n). Используется цикл с предусловием, в который вложена операция ветвления
|
Начало |
|
|
|
|
Ввод |
|
|
|
|
m, n |
|
|
|
нет |
m <> n |
да |
|
|
|
|
|
||
|
нет |
m > n |
да |
|
|
|
|
||
|
n=n-m |
|
|
m=m-n |
m=18 n=12 |
Вывод |
||
m |
|||
m=6 |
|
||
n=6 |
Конец |
||
НОД=6 |
|||
|
|||
|
ТРЕНИН |
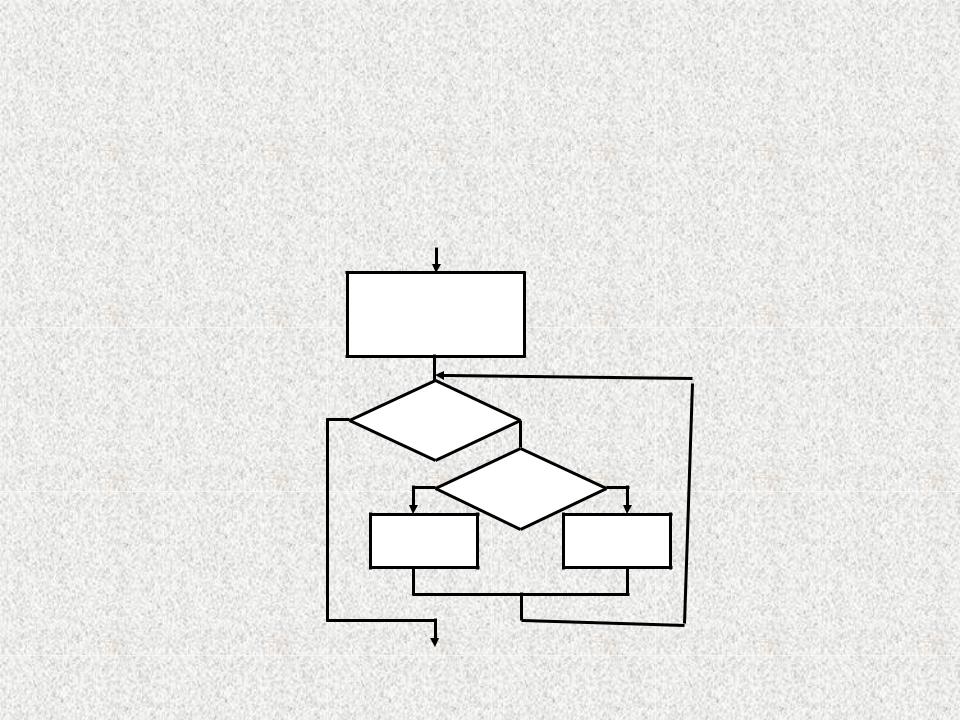
ПРИМЕР 1. |
Г |
Определите значение целочисленной переменной х после выполнения следующего фрагмента алгоритма:
|
x=55, |
|
|
|
y=75 |
|
|
нет |
x <> y |
да |
|
|
|
|
|
|
нет |
x > y |
да |
|
|
|
|
|
y=y-x |
|
x=x-y |
