Коэффициент перекрытия

Коэффициент торцевого перекрытия - это отношение угла торцевого перекрытия зубчатого колеса цилиндрической передачи к его угловому шагу, где под углом перекрытия понимают угол, на который поворачивается колесо за время зацепления одной пары зубьев.

Также коэффициентом перекрытия называют отношение длины k дуги зацепления к длине шага p_w по начальным окружностям колес

Коэффициент перекрытия характеризует плавность зацепления и показывает среднее число пар зубьев, находящихся одновременно в зацеплении. Чем больше коэффициент перекрытия, тем более плавно и бесшумно работает передача.

Коэффициентом перекрытия не должен быть меньше единицы, так как это приводит к перерывам в передаче движения от ведущего к ведомому и к ударам зубьев колес. Предельное значение коэффициента перекрытия в зубчатой передаче с нормальной высотой зуба равно 1,982. Если коэффициент перекрытия равен, например, 1,6, то это значит, что в среднем в зацеплении находится 1,6 пары зубьев, т.е. фактически 60% времени в зацеплении находятся две пары зубьев, а 40% - одна пара зубьев.

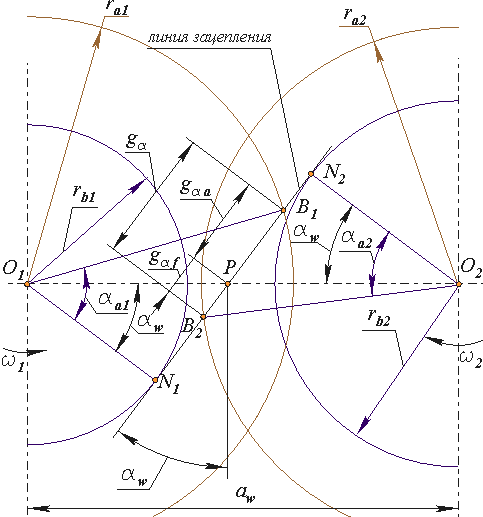
Рис. 7.8

Коэффициент формы зуба

 Геометрическая форма зуба в значительной мере определяет показатели его как изгибной, так и контактной прочности. Оценка влияния геометрии зуба на изгибную прочность осуществляется коэффициентом формы зуба Y. Этот коэффициент определяется через параметры балки параболического сечения (балки равного сопротивления изгибу), которая вписывается в контур зуба так, чтобы вершина параболы располагалась в точке пересечения оси зуба и нормали к профилю в вершине, а ветви касались профиля зуба у основания ( см. схему на рис.7.9).

где Sp - толщина зуба по хорде на окружности, проходящей через точки касания параболы и профиля зуба, l - высота от вершины параболы до хорды Sp .

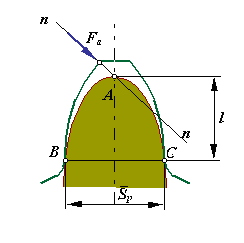
Рис 7.9

Коэффициент удельного давления.

Коэффициент удельного давления учитывает влияние геометрии зубьев (радиус кривизны их профилей) на величину контактных напряжений, возникающих в местах соприкосновения зубьев.

Коэффициентом удельного давления называется отношение модуля зацепления к приведенному радиусу кривизны эвольвентных профилей:

.

Коэффициенту имеет минималь­ное значение в середине теоретической линии зацепления N₁N₂ .

Коэффициент удельного скольжения.

Так как рабочие уча­стки профилей зубьев перекатываются друг по другу со скольжением, то на этих участках возникают силы трения и происходит процесс из­нашивания. Скорость скольжения в точке контакта профилей высшей пары определяется следующим выражением:

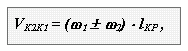
где l _КР - расстояние от точки контакта до полюса, знак "+" для внешнего зацепления,"-" для внутреннего.

Величина износа активных частей профилей в высшей паре в значительной степени зависит от их относительного скольжения и от скорости этого скольжения. Для оценки скольжения при геометрических расчетах зубчатых передач пользуются коэффициентом удельного скольжения

где V^tk_i - проекция скорости контактной точки звена i на контактную нормаль.

Графики изменения коэффициентов удельного давления и удельного скольжения по линии зацепления зубчатых колес.

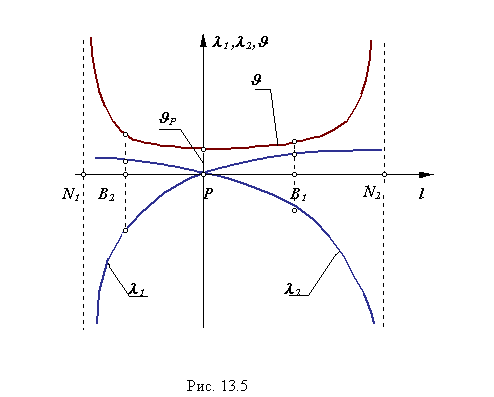
Рис. 7.10