14

Лекция 14

Тема: Динамика твердого тела

1. Кинетическая энергия системы. Вычисление кинетической энергии системы в общем виде.

2. Кинетическая энергия поступательного движения, вращательного движения.

3. Кинетическая энергия при плоскопараллельном движении.

4. Теорема об изменении кинетической энергии материальной точки.

5. Теорема об изменении кинетической энергии системы.

1. Кинетическая энергия системы. Теорема Кенига.

Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е. ().

Кинетическая энергия является скалярной положительной величиной. В системе СИ единицей измерения кинетической энергии является:

1 Дж=1Н∙м

Кинетическая энергия механической системы называется сумма кинетических энергий всех точек, входящих в систему:

(14.1)

Скорости точек системы определяются относительно неподвижной системы отсчета.

Совместим начало координат OXYZ с центром масс системы.

П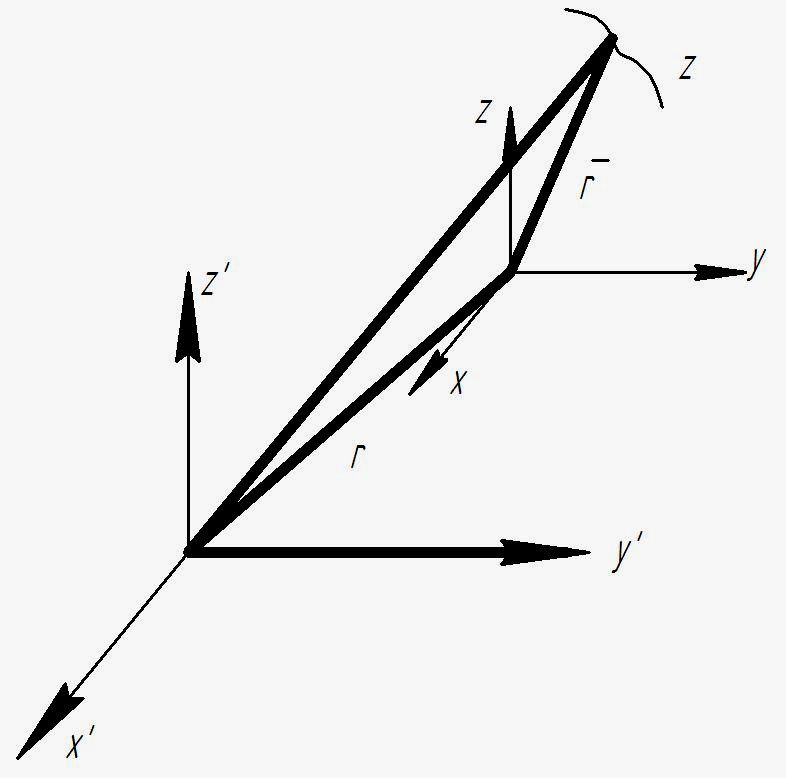редположим, что механическая система вместе с системой координат OXYZ движется поступательно относительно неподвижной системы координат O’X’Y’Z’. Точка р_к – точка системы.

Тогда на основании теоремы о сложении скоростей абсолютная скорость точки р_к заменяется как векторная сумма переносной и относительной скоростей.

(а)

где -переносная скорость, т.е. скорость центра масс

-относительная скорость

Подставляя (а) в (14.1) получаем:

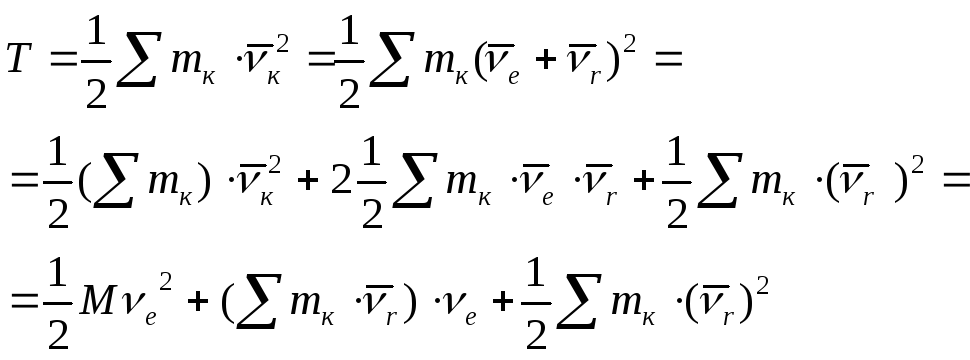
где - вся масса системы;

- радиус-вектор центра масс в подвижной системе координат.

Откуда:

, т.е.

Поскольку начало координат О совпадает с центром масс системы, то , тогда , т.е. векторная сумма равна нулю.

Таким образом, кинетическая энергия системы имеет вид:

Это равенство определяет теорему Кенига.

Кинетическая энергия системы равна сумме кинетической энергии, которую имела бы материальная точка, расположенная в центре масс системы и имеющая массу, равную массе системы и кинетической энергии движения системы относительно центра масс.

2. Кинетическая энергия твердого тела.

Твердое тело является частным случаем механической системы и рассматривается как непрерывно распределенная масса, тогда формула примет вид:

а) Кинетическая энергия твердого тела, движущегося поступательно.

П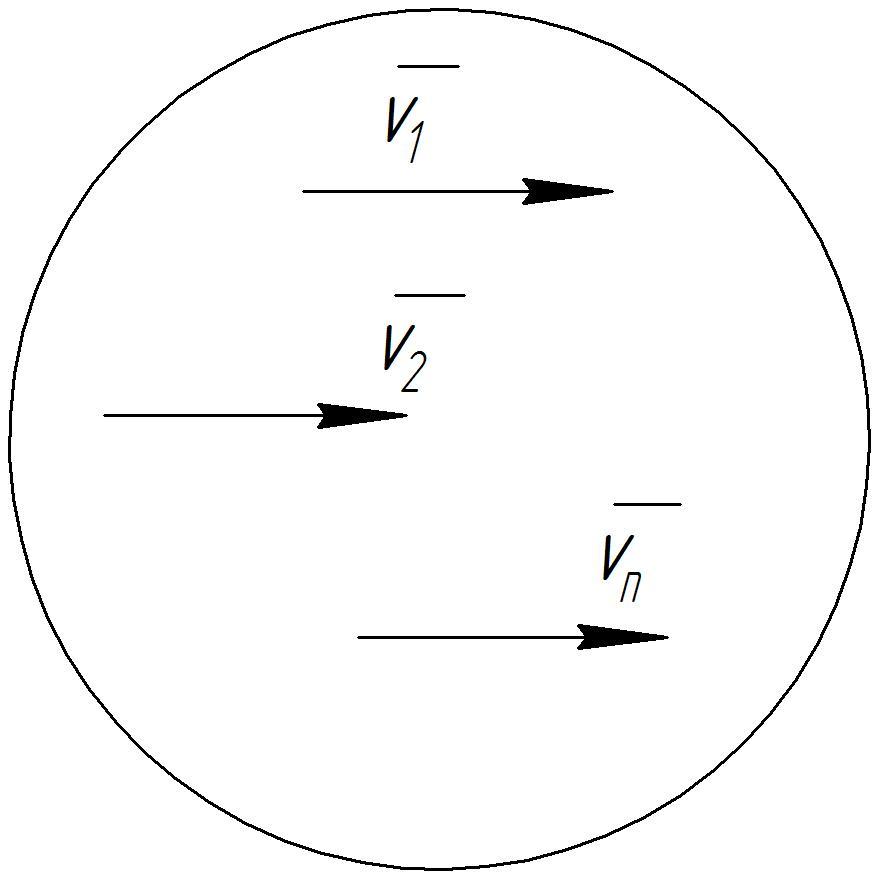ри этом движении скорости всех точек тела одинаковы.

Вынося в формуле за знак интеграла получим:

Кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела М на квадрат его скорости.

б) Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси.

М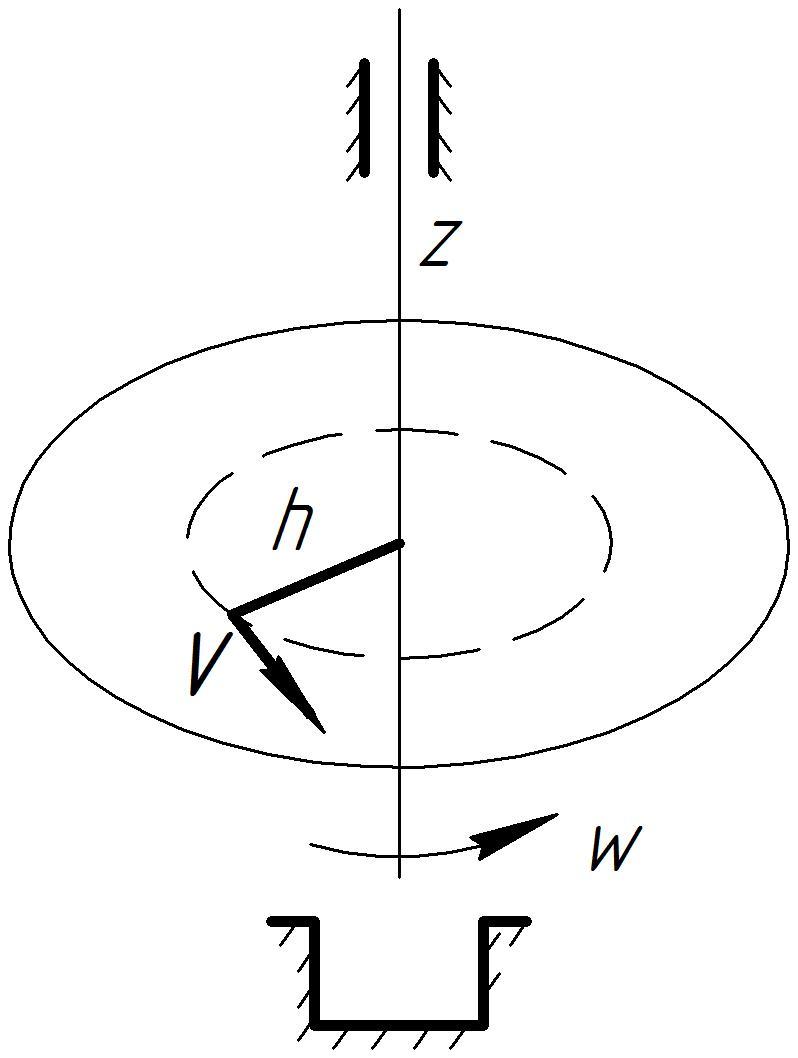одуль скорости v любой точки твердого тела, вращающегося вокруг неподвижной оси, равен w∙h, где w- модуль угловой скорости твердого тела, h-расстояние от точки до оси вращения z.

Подставляя v =w∙h в формулу , получим:

где - момент инерции твердого тела.

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.

3. Кинетическая энергия твердого тела при плоскопараллельном движении.

При плоскопараллельном движении скорость любой точки тела состоит из геометрической суммы скорости полюса и скорости точки при вращении вокруг полюса.

Пусть тело движется плоско в плоскости OXY, тогда || OZ. За полюс выбираем центр масс тела, тогда в формуле при ее вращении относительно полюса n равна:

где - расстояние k-ой точки до полюса

Тогда:

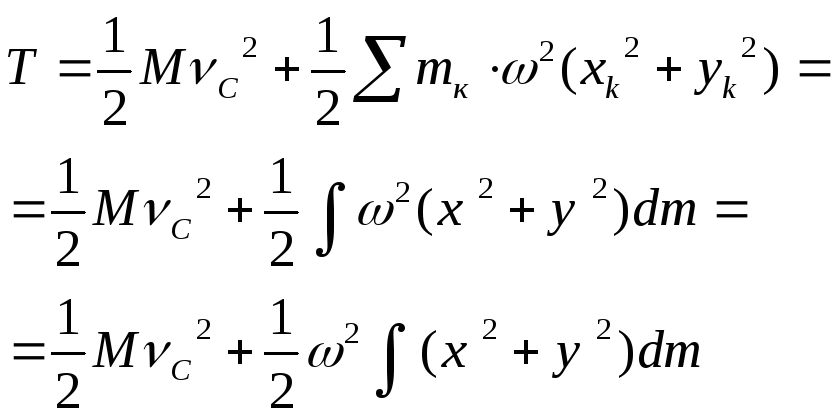
- момент инерции тела относительно оси OZ, проходящей через полюс С. Тогда:

При плоскопараллельном движении тела кинетическая энергия складывается из кинетической энергии поступательного движения вместе с центром масс и перпендикулярной плоскости движения

4. Теорема об изменении кинетической энергии.

Найдем связь между работой и изменением скорости. Пусть материальная точка массой m перемещается вдоль оси OХ под действием силы, например сжатой или разжатой пружины, закрепленной в начале координат, - точке О.

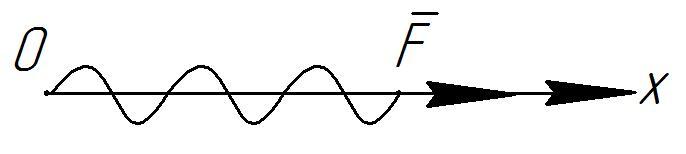Управление движения точки имеет вид:

Пусть v=v(x)

Подставим в формулу

Разделим переменные

В этом виде равенство имеет очень наглядный смысл: при смещении точки на dx сила совершает работу , в результате чего изменяется величина кинетической энергии точки , характеризующая движение точки и, в частности, модуль ее скорости.

Если точка смещается из положения х₁ в х₂, а скорость при этом изменяется от до , то, интегрируя, имеем:

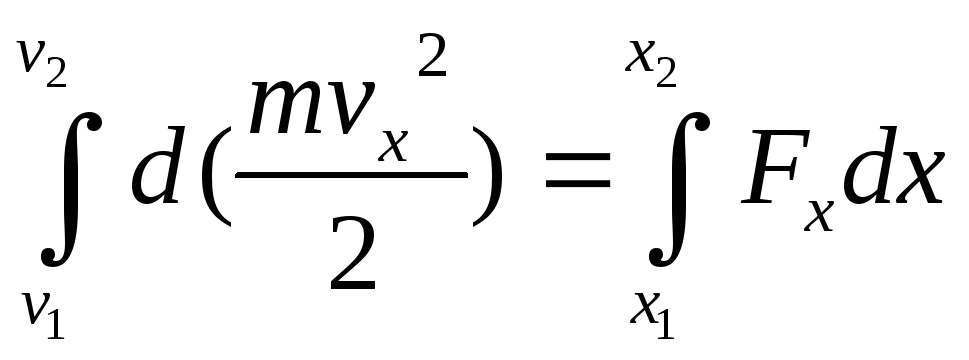
Учитывая, что

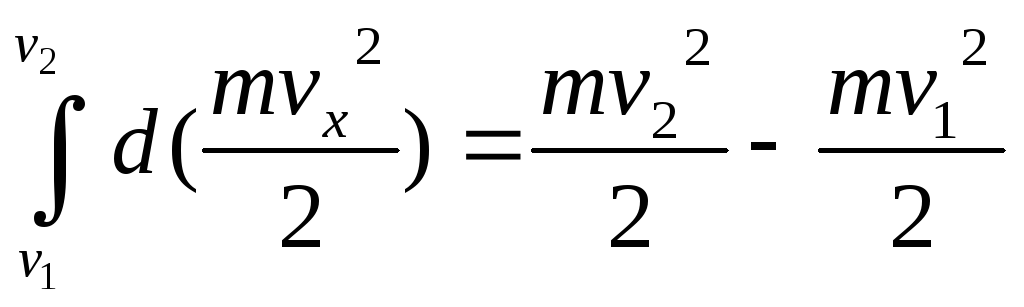
Окончательно находим

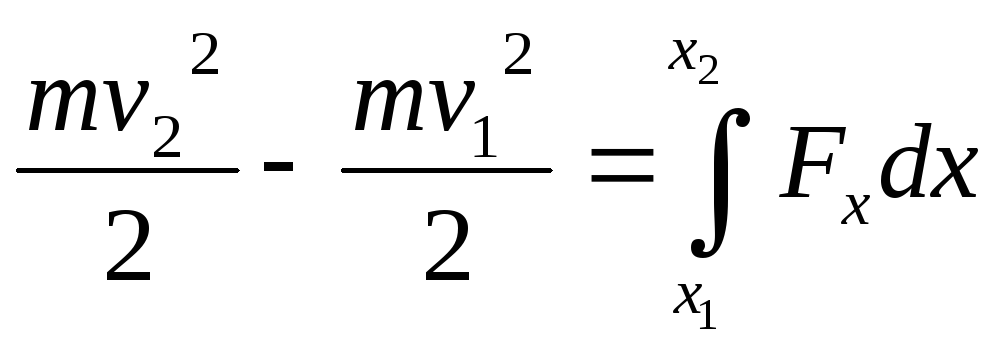
Изменение кинетической энергии материальной точки при ее каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.

5. Теорема об изменении кинетической энергии системы.

Кинетическая энергия системы:

Вычислим дифференциал кинетической энергии системы и преобразуем полученное выражение:

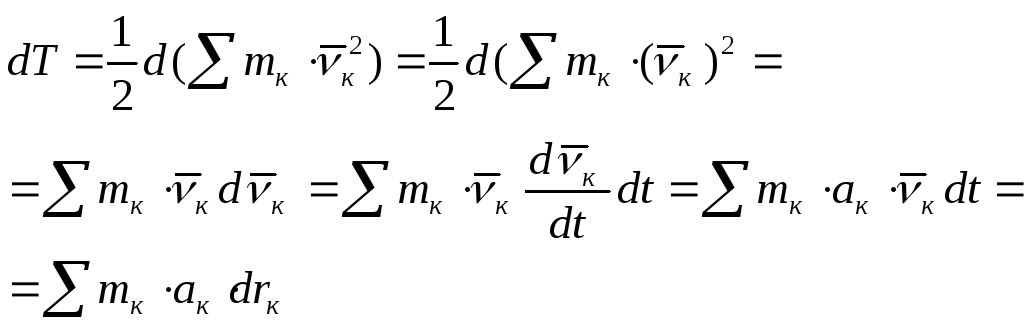
Здесь ;

Учитывая, что

где а_к – ускорение точки

- равнодействующая внешних и внутренних сил, приложенных к точке.

Таким образом:

Теорема об изменении кинетической энергии системы в дифференциальной теории.

Дифференциал кинетической энергии системы равен элементарной работе всех сил системы.

а) если для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:

то

Изменение кинетической энергии твердого тела при каком-либо элементарном перемещении равно элементарной работе внешних сил, действующих на тело.

Если обе части проинтегрировать между двумя положениями – начальным и конечным, в которых соответственно кинетическая энергия Т₁ и Т₂, получим: