4

Лекция №4

План:

1) Эквивалентность пар сил. Векторный момент пар сил

2) Приведение системы сил к центру.

3) Приведение системы сил, произвольно расположенных в пространстве к силе, к паре.

4) Главный вектор и главный момент. Вычисление главного вектора и главного момента.

1) Эквивалентность пар сил. Векторный момент пары сил.

Сформулируем условия эквивалентности двух пар сил, используя наиболее общую характеристику пары сил - ее векторный момент.

Известно, что пару сил можно поворачивать и переносить в плоскости её действия. От этого действие пары сил на твердое тело не изменяется, если алгебраический момент пары сил, остается таким же.

Следовательно, векторный момент пары сил можно переносить параллельно самому себе в любую точку твердого тела, лежащую в плоском действии пары сил. Так как пару сил можно переносить в параллельную плоскость, то векторный момент пары сил можно переносить параллельно самому себе в любую точку тела, не изменяя действия пары сил на твердое тело.

Поэтому векторный момент пары сил, действующий на твердое тело, есть свободный вектор, т.е. он характеризуется только величиной и направлением, а точкой приложения у него может быть любая точка и, векторный момент пары сил не обязательно прикладывается посередине отрезка, соединяющего точки приложения сил пар.

2) Приведение сил к заданному центру

Рассмотрим систему состоящую из любого количества сил, как угодно расположенных в пространстве. Такую систему сил будем называть произвольной пространственной системой сил. Прежде чем перейти к её преобразованию, приведем вспомогательную теорему о параллельном переносе сил

Теорема: Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого его действия на тело, переносить параллельно ей самой в любую точку тела, добавляя при этом пару с моментом, равным моменту переносимой силы, относительно новой точки ее приложения.

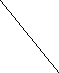
Доказательство: Пусть имеем силу F, приложенную в точке А. Известно, что силу, приложенную к твердому телу, можно переносить вдоль её линии действия, от чего действие силы на твердое тело не изменяется. Теперь докажем, что силу можно переносить на другую параллельную линию действия. Но этот перенос, следует компенсировать добавлением соответствующей пары сил. 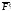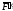Приложим в точку В, выбранной за центр приведения, систему двух равных по величине, но противоположных по направлению сил и параллельных заданной силе 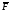. Система сил и ее можно добавить к любой заданной системе сил .

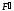
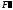
В

A

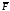
Тогда 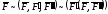Система сил называется присоединенной парой. Итак вместо силы F, приложенной в точке А получена сила F’, равная ей по величине и направлению, но приложенная в точке В и присоединенная пара сил (F, F’’) векторный момент которой

Процесс замены силы силой и парой сил (F, F’’) называется приведением силы к заданному центру.

Итак, если рассматривается система сил, то все силы( пользуясь данной теоремой) можно привести к некоторому центру – в этом и состоит метод, предложенный Пуансо.

Луи Пуансо (1777-1859 г.) французский математик, механик, автор геометрической статики (1803 г.). Ввел в механику понятие момента силы, пары сил, разработал теорию пар и метод приведения системы сил. Много сделал в кинематике, динамике.

3)Приведение системы сил, произвольно расположенных в пространстве к силе и паре

Теорема: Любую произвольную систему сил, действующих на твердое тело, можно в общем случае привести к силе и паре сил. При этом сила равна главному вектору системы сил и приложена в центре приведения, а пара имеет момент равный главному моменту системы сил, относительно центра приведения.

Доказательство: Пусть дана произвольная система сил - приложенная к твердому телу.

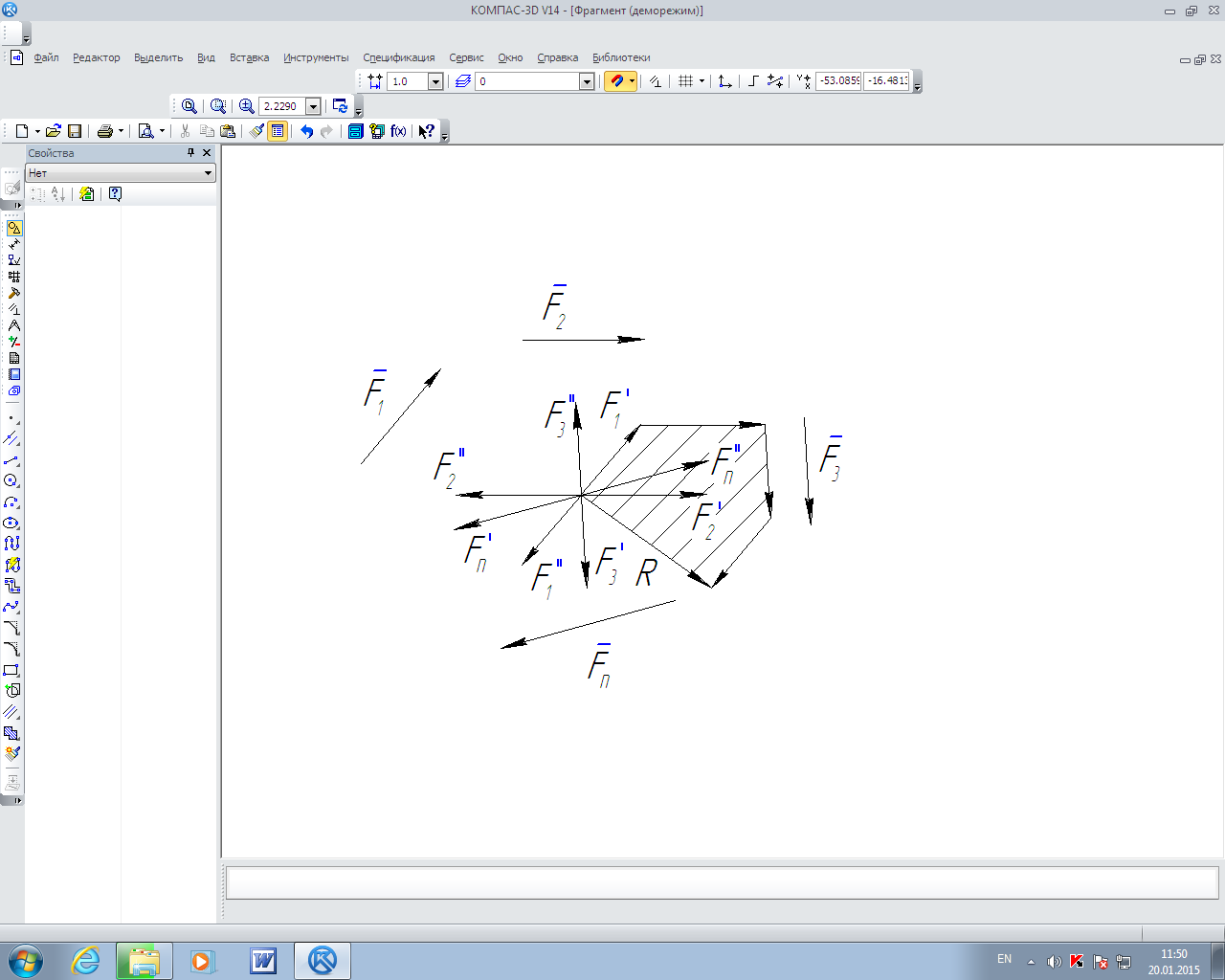
Выберем произвольную точку О за центр приведения и каждую силу заданной системы сил приведем к точке О, добавляя при каждом переносе присоединенную пару с моментом, равным моменту данной силы, относительно точки О. Таким образом система из n сил заменена системой из 3n сил, т.е. в точке О приложена система сходящихся сил и на твердое тело действует система n присоединенных пар сил

Векторный момент присоединенных пар сил можно выразить через векторные моменты заданных сил

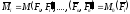
Образованную в точке О систему сходящихся сил 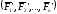. Заменим одной силой, их равнодействующей, равной векторной сумме 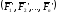~ R или

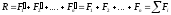
Геометрически изображается замыкающим вектором силового многоугольника, построенного на этих силах.

Для системы сходящихся сил 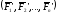сила R – равнодействующая .

Для заданной системы сил 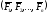сила R – векторная сумма или главный вектор

4) Главный вектор и главный момент. Вычисление главного вектора и главного момента

а) Главный вектор.

Для любой системы 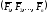сил главным вектором системы сил называется вектор, равный сумме этих сил:

Главный вектор геометрически изображается замыкающей силового многоугольника, построенного на заданных силах.

Проектируя обе части векторного равенства на координате оси, для произвольной, пространственной системы сил получаем:

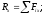
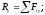
По проекциям определяем величину главного вектора и косинусы углов с осями координат.

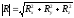
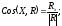
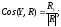
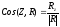
Для плоской системы сил, если выбрать ось OZ плоскости действия сил, то главный вектор R лежит в плоскости OXY и следовательно

;

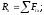
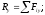
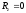
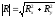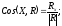
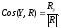
б) Главный момент сил.

Систему присоединенных пар 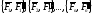сил можно по теореме о сложении пар сил заменить одной парой сил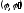 с векторным моментом.

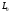,-называется главным моментом.

Главный момент 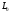равен сумме векторных моментов присоединенных пар

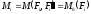
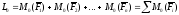
Индекс 0 у величины главного момента означает, что за центр приведения взята точка 0.

Итак, главный момент системы сил является вектором, замыкающим векторный многоугольник, образованный при сложении векторных моментов сил системы относительно выбранного центра

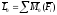
Проектируя обе части векторного равенства на прямоугольные оси координат и используя связь момента силы относительно оси с проекциями векторного момента этой силы относительно точки на оси, имеем:

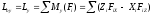
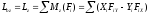
Величина главного момента и косинусы его углов с осями координат

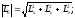
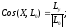
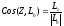
Для плоской системы сил, если ось OZ плоскости действия сил ось OX, OY в плоскости действия сил. Главный момент плоской системы сил главному вектору и параллелен оси OZ;