2

Лекция № 2.

План.

1. Момент силы относительно точки.

2. Момент силы относительно оси.

3. Аналитический метод вычисления моментов силы относительно осей координат.

4. Сложение параллельных сил, приложенных к твердому телу направленных в одну сторону.

5. Сложение параллельных сил, приложенных к твердому телу направленных в разные стороны ( антипараллельные силы).

6. Пара сил и её момент. Теорема о моменте сил пары относительно произвольной точки

1. ВОПРОС

1. Момент силы относительно точки.

Для характеристики вращательного движения под действием силы вводится понятие момента силы относительно точки.

Моментом силы относительно точки называется вектор равный векторному произведению радиуса-вектора, соединяющего центр O с точкой приложения силы точки А, на саму силу .

(1)

Момент силы относительно центра в плоскости.

Сила F в плоскости XOY

Момент направлен вдоль оси OZ

- алгебраическое значение момента в плоскости системы сил и модуль

определяется численно удвоенной площадью ∆ OAB

где h-плечо

Вычислим аналитически. Пусть заданы проекции радиус-вектора и проекция силы

Раскроем векторные произведения по формуле векторной алгебры:

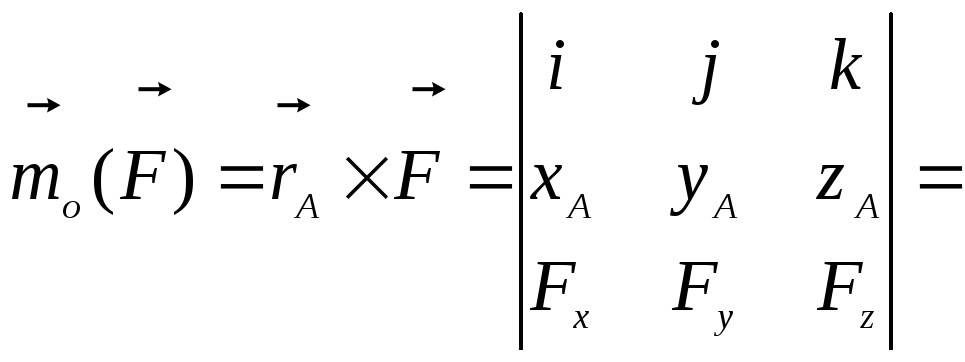
(2)

-единичные орты

где – координаты на оси .

2. Момент силы относительно оси.

Будем называть проекцию на эту ось вектора момента ,т. е. на оси .

С помощью формулы (2) момент силы относительно оси можно вычислить, зная проекции силы и координаты точки ее приложения.

Зная момент силы относительно осей можно определить модуль момента силы

3. Аналитический метод вычисления моментов силы относительно осей координат.

а)если сила параллельна оси, то её момент относительно этой оси равна нулю.

F // z

= 0

б) если линия действия силы пересекает оси, то её моменты относительно этих осей также равны нулю.

в) если сила перпендикулярна к оси, например к оси Y, и кратчайшее расстояние между линией действия силы и осью, например осью x,равно h,то момент силы относительно оси х равен произведению модуля силы на расстояние между линией действия силы и осью.

г) если сила старается развернуть твердое тело вокруг оси против хода часовой стрелки относительно наблюдателя, стоящего на этой оси, то момент силы относительно этой оси положительный рис.а); если по ходу часовой стрелки- отрицательный рис. б)

а) б)

4. Сложение параллельных сил, приложенных к твердому телу направленных в одну сторону.

Найдем равнодействующую 2х параллельных сил ,приложенных в точке А и точке В твердого тела

Разложим силу на 2 составляющие.Одну составляющую направим вдоль линии действия.Другую найдем по модулю и направлению с помощью силового треугольника рис.(а).Аналогично найдемс помощью силового треугольника рис.(б) и сходятся в точке О оба построения рис. (а и б) соединим в рис. (с) таким образом, вместо системы 2-х сил имеем эквивалентную из 4-(x) сил

Найдем равнодействующую из 4-х сил, так как равны по модулю и действуют вдоль одной линии, противоположно направлены, то они уравновешены и их сумма равна нулю.

Геометрическая сумма

Равнодействующая 2-х действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону равна по модулю сумме модулей слагаемых сил, им параллельна и направлена в ту же сторону.

Найдем линию действия равнодействующей, проведем через точку О прямую, параллельную линиям действия слагаемых сил. Точку пересечения этой прямой с АВ обозначим С.

Треугольник АСО подобен силовому треугольнику рис. (а), так как их стороны параллельны.

∆ ВСО подобен рис.(б)

Тогда и получим

Разделив почленно первую пропорцию на вторую и учтя, что получим

тогда

;

Итак

Линия действия равнодействующей 2-х действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону, проходят между точками приложения слагаемых сил на расстояниях от этих точек, обратно пропорционально модулям этих сил.

5. Сложение параллельных сил приложенных к твердому телу, направленных в разные стороны.

Рассмотрим тело, на которое действуют две параллельные силы направленные в противоположные стороны.

Возьмем на продолжении точку С. Приложим к ней две уравновешенные силы и // , так что и удовлетворялось равенство

Сложим силы

т.е. равна модулю

и эквивалентна 0 и их можно отбросить.

=> - равнодействующая.

Определение:

Равнодействующая 2-х антипараллельных сил равна по модулю разности модулей этих сил, им параллельна и направлена в сторону большей силы. Линия действия равнодействующей проходит вне отрезка соединяющего точку приложения слагаемых сил, на расстояниях от этих точек, обратно пропорционально модулям сил.

6. Пара сил и её момент силы.

Определение:

Две равные, параллельные, но противоположно направленные силы, приложенные в разных точках тела, наз парой сил. ; -пара сил

Пара сил создает вращательное действие на тело.

Пара сил характеризуется:

1)плоскостью действия сил.

2)направлением вращения пары сил в плоскости.

3)момент пары сил- это численная характеристика вращательного действия.

Момент пары равен произведению одной из сил пары (модуля) на плечо пары, взятого с определенным знаком.

Плечо пары : кратчайшее расстояние(d) между линиями действия сил, составляющих пару.

Момент пары сил положителен, если пары сил стремится вращать объект в сторону противоположную в ращению часовой стрелки рис.а) и отрицательным, если в сторону вращения часовой стрелки рис.б)

Вектор моментапары направлен перпендикулярно к плоскости действия пары сил в такую сторону, чтобы смотря навстречу этому вектору, видеть пару сил, стремящейся вращать плоскость её действия в сторону, обратную вращения часовой стрелки

Свойства пары сил

1. Пару сил, не изменяя её действия на твердое тело, можно переносить в любое место в плоскости её действия, поворачивать её плечо на любой угол.

2. Не изменяя действия пары сил на тело можно переносить эту пару в любую плоскость параллельную плоскости действия пары сил.

3. Н

   F

   е изменяя действие пары сил на твердое тело, можно изменять её силу и плечо,сохраняя неизменным модуль и направление её момента.

F

Теорема о моменте сил пары относительно произвольной точки:

С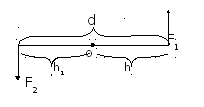умма моментов сил пары относительно любой точки, лежащей в плоскости действия пары равны моменту этой пары.