Свойства эквивалентности множеств:

1)

2. если то

3. если ато

Доказательство. 1) тождественное отображениеявляется взаимно однозначным; 2) есливзаимно однозначно, то– тоже; 3) еслии– взаимно однозначные отображения, то(– взаимно однозначное отображение.

Замечание. Нельзя назвать эквивалентность множеств отношением эквивалентности, потому что непонятно, на каком множестве рассматривается это отношение (такого понятия, как “множество всех множеств”, не существует).

Мощностью множества А называется совокупность всех множеств, эквивалентных множеству А. Мощность множества А обозначается

Теперь нам надо научиться сравнивать множества по мощности.

Говорят, что мощность множества не превосходит мощности множества(записываем:если существует вложение множества в множествоЕсли существует вложениевно не существует взаимно однозначного отображениянато мы говорим, что мощность множествастрого меньшемощности множестваи пишем

Очевидны следующие свойства:

1. 

2. 

Гораздо менее очевидным является свойство, называемое теоремой Шрёдера – Бернштейна:

Теорема 1 (теорема Шрёдера – Бернштейна). Если существуют вложенияито существует взаимно однозначное отображение

Доказательство. ПоложимПустьи вообщеМы имеем:

(1)

где

(2)

где Очевидно,взаимно однозначно отображаетнапоэтому существуеттакже взаимно однозначное. Проверим, чтовзаимно однозначно отображаетнаДействительно, пустьТак кактоСледовательно,ПустьТак какитодля некоторогоЭто равенство выполнено для каждого натуральногоЕслиито (ввиду того, что– вложение)Следовательно,Таким образом,взаимно однозначно. Кроме того,взаимно однозначно отображаетнанаи т.д., авзаимно однозначно отображаетнанаи т.д. Пользуясь соотношениями (1) и (2), нетрудно убедиться в том, что отображениеопределённое правилом

является взаимно однозначным. Теорема доказана.

Эта теорема, наряду с теоретическим значением, имеет большое практическое значение: она позволяет доказывать эквивалентность множеств ине прибегая к построению взаимно однозначного отображенияа строя лишь вложенияи

Пример. Докажем, что отрезоки интервалравномощны.

Действительно, тождественное отображение является вложениемвДалее, отрезоквкладывается в интервала он взаимно однозначно отображается на интервалс помощью отображенияОтсюда по теореме Шрёдера – Бернштейна получаем:

Итак, отношение обладает обычными свойствами частичного порядка (рефлексивность, транзитивность, антисимметричность). Возникает вопрос: любые ли два множества сравнимы по мощности? Другими словами, верно ли, что для любых множествихотя бы одно из них вкладывается в другое? Ответ здесь положительный:для любых множеств А и В имеет место хотя бы одно из следующих соотношений: но доказать это мы сможем лишь позже – в разделе 2.2.

Счётные множества

Множество называетсясчётным, если

Например, счётным является множество чётных натуральных чисел. Действительно, отображениезадаёт взаимно однозначное соответствие между множествамии

Свойства счётных множеств:

1. объединение двух счётных множеств счётно;

2. прямое произведение двух счётных множеств счётно;

3. объединение счётного числа счётных множеств счётно;

4. всякое бесконечное множество имеет счётное подмножество.

Доказательство. Докажем вначале свойство 2). Пустьгде– счётные множества. Элементы множестваможно расположить в следующем виде:

			. . .
			. . .
			. . .
. . .	. . .	. . .	. . .

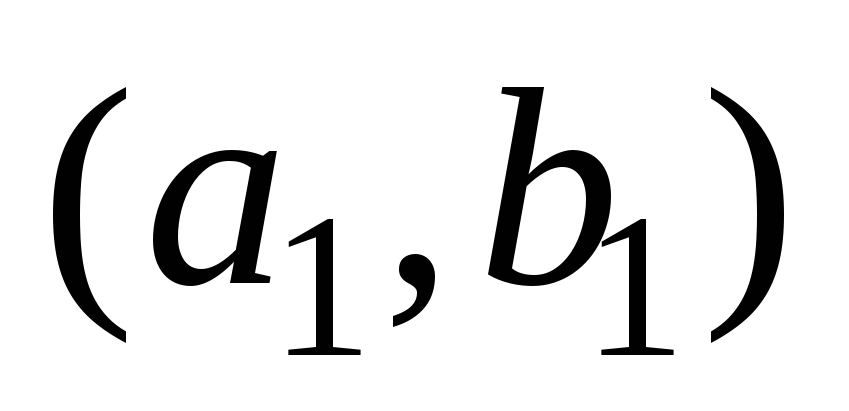
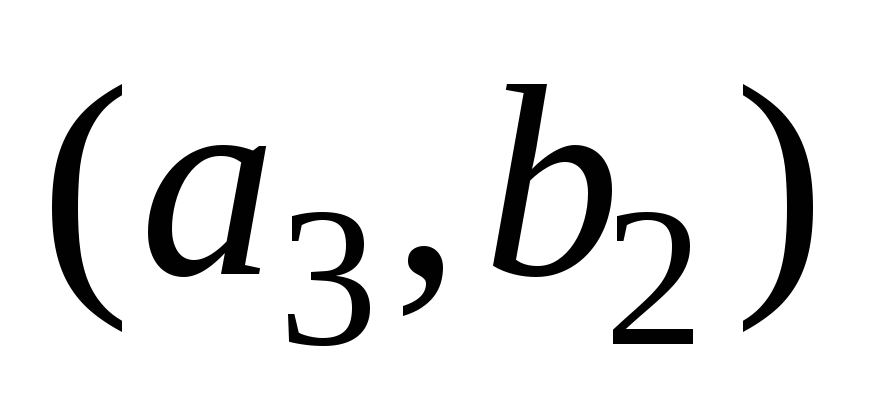
Пересчёт элементов множества т.е. установление взаимно однозначного соответствия между элементами множествиможет быть осуществлён, например, так:

1	2	4	7	11	16 . . .
3	5	8	12	17	23 . . .
6	9	13	18	24	31 . . .
10	14	19	25	32	40 . . .
15	20	25	33	41	50 . . .
21 . . .	27 . . .	34 . . .	42 . . .	51 . . .	61 . . . . . . . .

Номер, который будет присвоен паре равен

Свойство 3) следует из 2) и теоремы Шрёдера – Бернштейна. Поясним это. Пусть где каждоесчётно. Так каквкладывается втовкладывается вОсталось построить вложениеПо условиюсчётные множества, поэтомузначит, элемент изимеет видНе исключается, чтопри каких-нибудьДля каждоговыберем одно какое-нибудь представление в видеОтображениеопределяет вложениева по свойству 2)Значит,

Свойство 1) следует из 3), так как

Докажем свойство 4). Пусть бесконечное множество. Выберем элементТак какбесконечно, тоЗначит, существует элементТаким же образом найдёми т.д. Мы получили счётное подмножествомножества

Мощность множества (а значит, любого счётного множества) обозначается(читается: “алеф-нуль”). Так как всякое бесконечное множество содержит счётное подмножество, то– самая маленькая из всех бесконечных мощностей.

Если и– два непересекающихся счётных множества, то по свойству 1)Это можно записать так:Аналогично этому свойство 2) можно записать так:

Множество называетсянесчётным, если оно бесконечно и неэквивалентно счётному множеству (т.е. его мощность больше).

Теорема 2 (Кантора). Множествонесчётно.

Доказательство. Каждое числоимеет десятичную записьгдеПри этом некоторые числа могут быть записаны двумя способами, например,Из этих двух записей выберем первую, т.е. запретим ситуацию, когда в десятичной записи числа, начиная с некоторого момента, идут одни девятки. Исключением сделаем лишь число

Предположим, что множество счётно. Тогда

Представим в виде десятичной дроби:

Теперь построим число следующим образом. Пустьлюбая цифра, отличная оти 9,любая цифра, отличная оти 9, и вообщеПоложимТогдапри всехТак как, мы получили противоречие с равенствомТеорема доказана.

Замечание. Приведённый здесь метод доказательства называется диагональным методом Кантора.

Мощность множества чисел отрезка называетсямощностью континуумаи обозначаетсяс. Очевидно,с