
- •14. Ординальные числа. Арифметика ординалов.
- •15. Кардинальные числа. Мощность множества.
- •16. Теорема Кантора о мощности множества всех подмножеств данного множества
- •17. Теорема о том, что для бесконечной мощностиm.
- •18. Понятие моделей данной сигнатуры. Примеры. Формулы исчисления предикатов. Истинность формулы в данной модели
- •Примеры сигнатур:
- •19. Аксиомы Пеано натуральных чисел
- •20. Аксиомы действительных чисел
- •21. Выразимые предикаты. Элиминация кванторов.
- •22. Фильтры и ультрафильтры
- •23. Ультрапроизведение моделей. Истинность формул на ультрапроизведении. Th. Лося.
- •24. Локальная теорема Гёделя-Мальцева и следствие из неё.
- •25. Машины Тьюринга и вычислимые функции
- •26. Разрешимые и перечислимые множества. Их свойства.
- •27. Универсальные вычислимые функции
- •28. Существование перечислимого неразрешимого множества. Неразрешимость проблемы остановки машины Тьюринга.
24. Локальная теорема Гёделя-Мальцева и следствие из неё.
Предложением
мы будем называть замкнутую формулу,
т.е. формулу, не содержащую свободных
переменных. Теорией
будем называть совокупность предложений
(конечную или бесконечную) одной
сигнатуры. Будем говорить, что теория
![]() имеет модель
имеет модель
![]() если все предложения теории
если все предложения теории![]() истинны на
истинны на![]() Далее, если
Далее, если![]() – теория, а Ф – замкнутая формула УИП,
то мы пишем
– теория, а Ф – замкнутая формула УИП,
то мы пишем![]() если Ф истинна на любой модели теории
если Ф истинна на любой модели теории![]() т.е. Ф истинна на любой модели, на которой
истинны все формулы из
т.е. Ф истинна на любой модели, на которой
истинны все формулы из![]()
Теорема
5 (теорема
компактности
Гёделя – Мальцева).
Если каждое конечное подмножество
![]() имеет модель, то теория
имеет модель, то теория![]() имеет модель.
имеет модель.
Доказательство.
Пусть
![]() – множество всех конечных подмножеств
множества
– множество всех конечных подмножеств
множества![]() и
и![]() – модель для
– модель для![]() Для формулы
Для формулы![]() пусть
пусть![]() истинна на
истинна на![]() Проверим, что
Проверим, что![]() – центрированная система подмножеств
множества
– центрированная система подмножеств
множества![]() Действительно, рассмотрим конечное
подмножество
Действительно, рассмотрим конечное
подмножество![]() Тогда
Тогда![]() Значит, формулы
Значит, формулы![]() истинны на модели
истинны на модели![]() следовательно,
следовательно,![]() Таким образом,
Таким образом,![]() Мы показали, что
Мы показали, что![]() – центрированная система. По теореме
1 и теореме 2 эту систему можно вложить
в некоторый ультрафильтр
– центрированная система. По теореме
1 и теореме 2 эту систему можно вложить
в некоторый ультрафильтр![]() Рассмотрим ультрапроизведение
Рассмотрим ультрапроизведение![]() Пусть
Пусть![]() Тогда
Тогда![]() истинна на всех
истинна на всех![]() где
где![]() Но
Но![]() значит, по теореме Лося (Th.
Лося: Пусть
значит, по теореме Лося (Th.
Лося: Пусть
![]() – ультрапроизведение моделей
– ультрапроизведение моделей![]() одной и той же сигнатуры
одной и той же сигнатуры![]() Формула
Формула![]() данной сигнатуры истинна на наборе
данной сигнатуры истинна на наборе![]() в том и только в том случае, если
в том и только в том случае, если![]() )
)![]() истинна на ультрапроизведении
истинна на ультрапроизведении![]() Таким образом,G
является
моделью для
Таким образом,G
является
моделью для
![]()
Для доказательства неаксиоматизируемости некоторых классов алгебраических систем часто используется следствие из теоремы компактности, которое мы сейчас приведём.
Следствие.
Пусть
![]() – множество предложений логики первого
порядка и
– множество предложений логики первого
порядка и![]() Тогда существует конечное подмножество
Тогда существует конечное подмножество![]() такое, что
такое, что![]()
Доказательство.
Предположим противное, т.е. что
![]() для любого конечного
для любого конечного![]() Тогда для каждого конечного
Тогда для каждого конечного![]() существует модель, для которой предложение
существует модель, для которой предложение![]() истинно. По теореме компактности
существует модель, в которой все
предложения изT
и предложение
истинно. По теореме компактности
существует модель, в которой все
предложения изT
и предложение
![]() истинны. Но тогда
истинны. Но тогда![]() вопреки условию.
вопреки условию.
25. Машины Тьюринга и вычислимые функции
Машина Тьюринга так же, как и конечный автомат, является дискретным устройством преобразования информации. Приведём её точное определение, а затем интерпретацию её работы.
Машиной Тьюринга называется частичное отображение (множество состояний)
![]()
Где
![]() обозначает “лево”, “право”. Тот факт,
что отображение
обозначает “лево”, “право”. Тот факт,
что отображение![]() частичное, означает, что
частичное, означает, что![]() может быть определено не для всех наборов
аргументов. Машина Тьюринга
может быть определено не для всех наборов
аргументов. Машина Тьюринга![]() работает с бесконечной в обе стороны
лентой, разбитой на ячейки, в каждой из
которых написан один из символов 0, 1.
Считывающая головка машины обозревает
в каждый момент времени одну из ячеек
и за один такт, сменяющий два последовательных
момента времени, может перемещаться
влево или вправо. Машина Тьюринга в
каждый момент времени находится в одном
из состояний
работает с бесконечной в обе стороны
лентой, разбитой на ячейки, в каждой из
которых написан один из символов 0, 1.
Считывающая головка машины обозревает
в каждый момент времени одну из ячеек
и за один такт, сменяющий два последовательных
момента времени, может перемещаться
влево или вправо. Машина Тьюринга в
каждый момент времени находится в одном
из состояний![]() а в следующий момент времени переходит
в другое состояние или остаётся в том
же. Кроме того, машина может изменять
символ, стоящий в обозреваемой ячейке.
Все эти преобразования – изменение
состояния, информация на ленте, направление
движения полностью определяются
отображением
а в следующий момент времени переходит
в другое состояние или остаётся в том
же. Кроме того, машина может изменять
символ, стоящий в обозреваемой ячейке.
Все эти преобразования – изменение
состояния, информация на ленте, направление
движения полностью определяются
отображением![]() А именно, если
А именно, если![]() то в случае, когда машина находится в
состоянии
то в случае, когда машина находится в
состоянии![]() а на обозреваемой в данный момент ячейке
написан символ
а на обозреваемой в данный момент ячейке
написан символ![]() машина должна записать в эту ячейку
машина должна записать в эту ячейку![]() вместо
вместо![]() перейти в состояние
перейти в состояние![]() и сдвинуться на одну ячейкувлево.
Например, равенство
и сдвинуться на одну ячейкувлево.
Например, равенство
![]() означает, что, находясь в состоянии
означает, что, находясь в состоянии![]() и обозревая ячейку, в которой написан
символ 1, машина должна сохранить в этой
ячейке символ 1, сдвинуться вправо и
перейти в состояние
и обозревая ячейку, в которой написан
символ 1, машина должна сохранить в этой
ячейке символ 1, сдвинуться вправо и
перейти в состояние![]() Если же
Если же![]() не определено, то машина, находясь в
состоянии
не определено, то машина, находясь в
состоянии![]() и обозревая ячейку с символом
и обозревая ячейку с символом![]() прекращает работу, не изменяя своего
состояния, информации на ленте и никуда
не сдвигаясь.
прекращает работу, не изменяя своего
состояния, информации на ленте и никуда
не сдвигаясь.
Более
удобна запись программы,
которая заключает в себе всю информацию
о работе машины (таким образом, задания
машины с помощью отображения и с помощью
программы эквивалентны между собой).
Опишем составление программы. Для
каждого равенства вида
![]() где
где![]() номера состояний,
номера состояний,![]() направление движения, а
направление движения, а![]() символы на ленте, запишем строку
символы на ленте, запишем строку![]() и назовём еёкомандой.
Совокупность всех команд – это и есть
программа. Если
и назовём еёкомандой.
Совокупность всех команд – это и есть
программа. Если
![]() не определено, то в программе нет ни
одной команды, начинающейся с
не определено, то в программе нет ни
одной команды, начинающейся с![]() Кроме того, для любых
Кроме того, для любых![]() в программе есть не более одной команды,
начинающейся с
в программе есть не более одной команды,
начинающейся с![]()
Будем
говорить, что машина
Тьюринга
![]() вычисляет функцию
вычисляет функцию
![]() если для любого набора
если для любого набора![]() натуральных чисел машина
натуральных чисел машина![]() находясь в состоянии
находясь в состоянии![]() и обозревая крайнюю левую единицу в
и обозревая крайнюю левую единицу в![]() (причём [xi]=i+1
единиц, как и значение f
)останавливается в том и только в том
случае, когда значение
(причём [xi]=i+1
единиц, как и значение f
)останавливается в том и только в том
случае, когда значение
![]() определено, и в конце работы ленте
должно быть записано ...0
определено, и в конце работы ленте
должно быть записано ...0![]() 0...,
а считывающая головка машины должна
стоять напротив крайней левой единицы.
0...,
а считывающая головка машины должна
стоять напротив крайней левой единицы.
Таким
образом, если, например,
![]() то мы должны иметь
то мы должны иметь
![]()
а
если
![]() не существует, то машина, запущенная на
ленте
не существует, то машина, запущенная на
ленте![]() должна работать бесконечно долго (при
условии, что начальное состояние
должна работать бесконечно долго (при
условии, что начальное состояние![]() а обозреваемая в начальный момент
времени ячейка – крайняя левая единица.
а обозреваемая в начальный момент
времени ячейка – крайняя левая единица.
Если
информация на ленте не имеет вид
![]() или начальное состояние не
или начальное состояние не![]() или обозреваемая ячейка – не крайняя
левая единица, то поведение машины может
быть каким угодно.
или обозреваемая ячейка – не крайняя
левая единица, то поведение машины может
быть каким угодно.
Рекурсивные
функции. Напомним,
что в этой главе множество N
натуральных чисел содержит 0, т.е.
![]() Будем рассматривать функции (возможно,
частичные)
Будем рассматривать функции (возможно,
частичные)
![]()
![]() Таким образом, если
Таким образом, если![]() то либо
то либо![]() либо
либо![]() не определено. Введём в рассмотрениепростейшие
функции о
не определено. Введём в рассмотрениепростейшие
функции о![]() s
s![]() I
I![]()
Эти ф-ции могут быть вычислены с помощью соотв. механического устройства (например, на м. Тьюринга). Определим операторы, кот. по одной или неск-ким заданным функциям строят новые ф-ции.
Оператор
суперпозиции.
Пусть даны функция
![]() от
от![]() переменных и
переменных и![]() функций
функций![]() от
от![]() переменных.. Суперпозицией функций
переменных.. Суперпозицией функций![]() называется функция
называется функция
![]()
Мы
говорим, что функция
![]() получается применением оператора
суперпозиции
получается применением оператора
суперпозиции
![]() к функциям
к функциям
![]() и пишем
и пишем
![]()
Например,
![]() (s,o)
– это функция
(s,o)
– это функция
![]() s(o
s(o![]() т.е. функция, тождественно равная 1, а
т.е. функция, тождественно равная 1, а
![]() (s,s)
– это функция
(s,s)
– это функция
![]()
Оператор
примитивной рекурсии.
Пусть даны функции
![]() и
и![]() Построим функцию
Построим функцию![]() Пусть зафиксированы значения
Пусть зафиксированы значения![]() Тогда положим:
Тогда положим:
![]()
Эти
равенства определяют функцию
![]() однозначно. Функция
однозначно. Функция![]() называется функцией, полученной с
помощью оператора
называется функцией, полученной с
помощью оператора
![]() примитивной рекурсии. Используется
запись
примитивной рекурсии. Используется
запись
![]()
Индуктивное
определение функции (продемонстрированное
в операторе примитивной рекурсии) в
математике не редкость. Например,
индуктивно определяются степень с
натуральным показателем:
![]()
![]() факториал:
факториал:![]()
![]() и т.д.
и т.д.
Функции,
которые могут быть получены из простейших
о![]() s
s![]() I
I![]() применением конечного числа раз
операторов суперпозиции и примитивной
рекурсии, называются примитивно
рекурсивными.
(примитивно рекурсивные функции всюду
определен, т.е.
определены для всех значений их
аргументов). Существенно более широким
классом функций, чем примитивно
рекурсивные функции, является класс
рекурсивных
функций (определение см. ниже). В
литературе эти функции называют также
частично
рекурсивными.
Для их определения введём ещё один
оператор.
применением конечного числа раз
операторов суперпозиции и примитивной
рекурсии, называются примитивно
рекурсивными.
(примитивно рекурсивные функции всюду
определен, т.е.
определены для всех значений их
аргументов). Существенно более широким
классом функций, чем примитивно
рекурсивные функции, является класс
рекурсивных
функций (определение см. ниже). В
литературе эти функции называют также
частично
рекурсивными.
Для их определения введём ещё один
оператор.
Оператор
минимизации.
Пусть дана функция
![]() Зафиксируем какие-либо значения
Зафиксируем какие-либо значения![]() первых
первых![]() переменных и будем вычислять
переменных и будем вычислять![]()
![]() и т.д. Если
и т.д. Если![]() наименьшее натуральное число, для
которого
наименьшее натуральное число, для
которого![]() (т.е. значения
(т.е. значения![]()
![]() все существуют и не равны
все существуют и не равны![]() то полагаем
то полагаем![]() Таким образом,
Таким образом,
![]()
![]()
Если
такого
![]() нет, то считаем, что
нет, то считаем, что![]() не определено. Итак, возможны три случая:
не определено. Итак, возможны три случая:
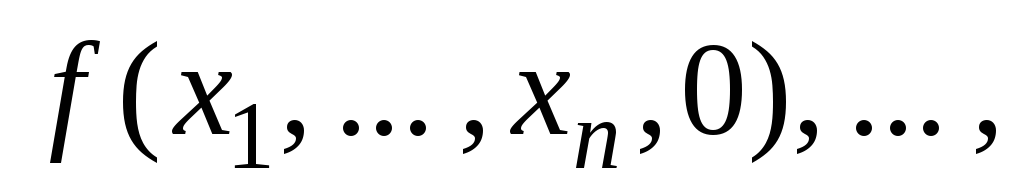
 существуют
и не равны
существуют
и не равны
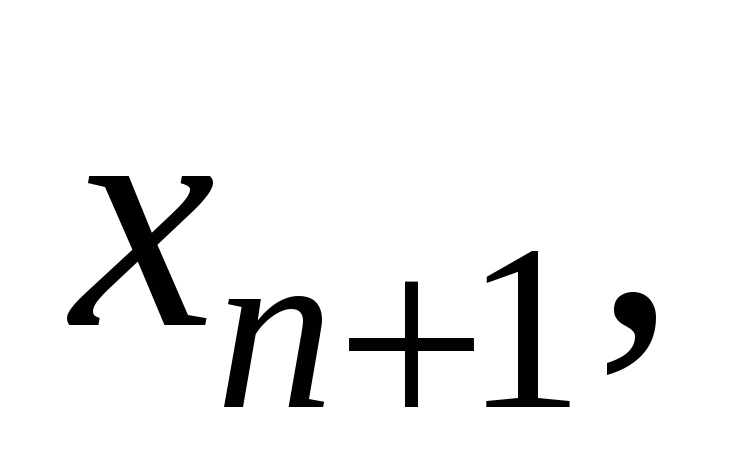 а
а

 существуют
и не равны
существуют
и не равны
 а
а не существует;
не существует; существуют
при всех
существуют
при всех
 и отличны от
и отличны от
Если
имеет место 1-й случай, то
![]() а если 2-й или 3-й, то
а если 2-й или 3-й, то![]() не определено. Про функцию
не определено. Про функцию![]() полученную таким образом, говорят, что
она получена из
полученную таким образом, говорят, что
она получена из![]() применением оператора минимизации
применением оператора минимизации![]() Мы пишем
Мы пишем![]()
Оператор
минимизации – это очевидное обобщение
оператора взятия обратной функции.
Обобщение довольно глубокое, так как
от функции
![]() не требуется, чтобы она была взаимно
однозначной (по переменной
не требуется, чтобы она была взаимно
однозначной (по переменной![]()
Функции,
которые могут быть получены из простейших
о![]() s
s![]() I
I![]() применением конечного числа раз
операторов суперпозиции, примитивной
рекурсии и минимизации, называются
рекурсивными.
Рекурсивные функции отражают наше
интуитивное представление о функциях,
вычислимых некоторым механическим
устройством. В частности, они вычислимы
на машинах Тьюринга (см. предыдущий
раздел). Наоборот, всякая функция,
вычислимая на машине Тьюринга, рекурсивна.
В предыдущем разделе, впрочем, были
построены машины Тьюринга, реализующие
функции o
применением конечного числа раз
операторов суперпозиции, примитивной
рекурсии и минимизации, называются
рекурсивными.
Рекурсивные функции отражают наше
интуитивное представление о функциях,
вычислимых некоторым механическим
устройством. В частности, они вычислимы
на машинах Тьюринга (см. предыдущий
раздел). Наоборот, всякая функция,
вычислимая на машине Тьюринга, рекурсивна.
В предыдущем разделе, впрочем, были
построены машины Тьюринга, реализующие
функции o![]() s
s![]() I
I![]() С другой стороны, не всякая функция
натуральных аргументов и даже не всякая
функция одного аргумента является
рекурсивной,. В самом деле, рекурсивных
функций имеется лишь счётное число
(т.е. их можно занумеровать натуральными
числами), а все функции
С другой стороны, не всякая функция
натуральных аргументов и даже не всякая
функция одного аргумента является
рекурсивной,. В самом деле, рекурсивных
функций имеется лишь счётное число
(т.е. их можно занумеровать натуральными
числами), а все функции
![]() образуют несчётное множество. Существование
нерекурсивных функций и является
“математической причиной” наличия
алгоритмически неразрешимых задач.
образуют несчётное множество. Существование
нерекурсивных функций и является
“математической причиной” наличия
алгоритмически неразрешимых задач.
