19. Аксиомы Пеано натуральных чисел

Множеством натуральных чисел мы будем называть любое множество на котором определена операция следования(элементинтерпретируется как элемент множестванепосредственно следующий за элементоми выполняется ряд аксиом(аксиомы Пеано). Для простоты мы будем пока равенство понимать как совпадение элементови(не описывать аксиоматически отношение равенства).

Аксиомы Пеано:

(П1) (аксиома наличия наименьшего элемента);

(П2)

(П3) (аксиома индукции). Пусть – подмножество множестватакое, что выполняются условия:

(а)

(б)

Тогда

Определим сложение двух натуральных чисел. Пусть Положим:при(индуктивное определение). Ввиду аксиомы индукции мы можем считать, что определено для всех

Докажем свойство коммутативности натуральных чисел, т.е. что Для этого нам понадобятся две леммы.

Лемма 1. Доказательство проведём индукцией по Приутверждение очевидно. Пустьдокажем, чтоИмеем:

Лемма 2. для любыхДоказательство. Индукция по Приполучаем:Пустьпри всехи некоторомДокажем, что то же верно дляИмеем:что и требовалось.

Теорема 1. при всехДоказательство. Индукция по Приутверждение следует из леммы 1. Пустьпри всехи некоторомДокажем, что то же верно дляИмеем (с учётом предположения индукции и леммы 2):Теорема доказана. Аналогично доказывается закон ассоциативности

На множестве натуральных чисел можно определитьотношение порядка: а такжеоперацию умножения: С помощью аксиом Пеано можно доказатьзаконы ассоциативности икоммутативности умножения, а также закон дистрибутивности Доказываются такжесвойства неравенств: и многие другие. Тем самым аксиомы Пеано позволяют построить строгую и стройную теорию натуральных чисел.

Заметим, что любое множество (независимо от его природы) мы называем множеством натуральных чисел, если оно удовлетворяет аксиомам Пеано. Любые два “множества натуральных чисел” (т.е. два множества А и В, удовлетворяющие аксиомам Пеано) изоморфны друг другу, т.е. существует взаимно однозначное соответствие сохраняющее операцию следования:Значит,множество натуральных чисел единственно с точностью до изоморфизма. Для других аксиоматических систем ситуация может быть совсем иной. Например, аксиомы группы не определяют объект однозначно с точностью до изоморфизма. В самом деле, две неизоморфные группы удовлетворяют аксиомам группы (ассоциативность, наличие единицы, наличие обратного элемента).

Теорема 2. Любые два множества А и В, удовлетворяющие аксиомам (П1) – (П3), изоморфны друг другу.

Доказательство. Ввиду аксиомы (П1) в А есть наименьший элемент а вВ – наименьший элемент Построим индуктивно отображениеПоложими вообще, еслито положимПо аксиоме (П3)продолжается до всегоА и По аксиоме (П2)взаимно однозначно. Равенствоследует из определения отображения

20. Аксиомы действительных чисел

Множество действительных чисел мы будем рассматривать как множество, на котором определены операция сложения умножения отношение порядка и выполняются аксиомы:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

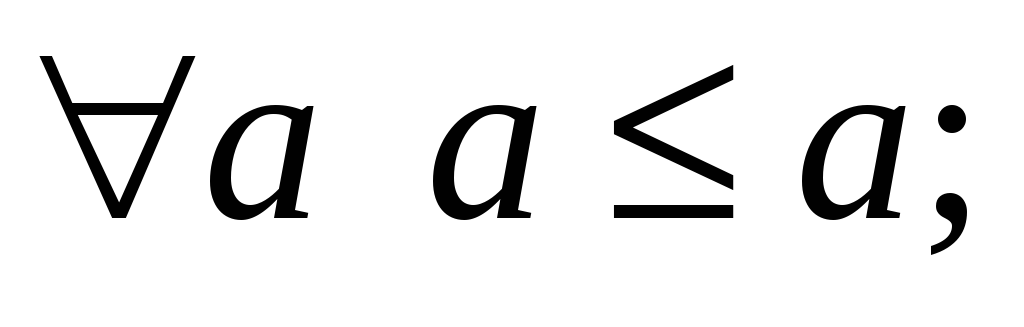
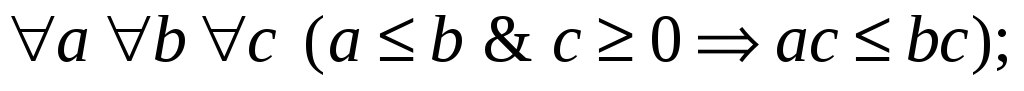
16. (аксиома Архимеда). Каковы бы ни были действительные числа существует натуральное числотакое, что

17. (аксиома непрерывности). Если – непустые подмножества множества действительных чисел ипри всехто существует действительное числотакое, что(т.е.при

Как видно, по форме построения аксиомы (16) и (17) отличаются от других аксиом. Правда, аксиому Архимеда можно переписать так: а аксиома непрерывности переписывается так:

R

Но, в отличие от аксиом (1) – (15), не все кванторы имеют областью определения множество действительных чисел: в аксиоме Архимеда квантор действует на натуральные числа, а в аксиоме непрерывности – на подмножества. Мы будем говорить, что аксиомы (1) – (15) являются формулами логики первого порядка, а аксиомы (16), (17) таковыми не являются (точные определения будут даны в следующем разделе).

В курсе математического анализа доказывается, что аксиома непрерывности эквивалентна принципу вложенных отрезков, а также теореме о существовании точной верхней грани непустого ограниченного множества. Следовательно, аксиома (17) может быть заменена на одно из этих утверждений.

Отметим, что множество действительных чисел определяется аксиомами (1) – (17) однозначно с точностью до изоморфизма. Однако доказывать это утверждение мы не будем. Аксиом (1) – (16) для определения множества недостаточно, так как этим аксиомам удовлетворяет также множестворациональных чисел. Кроме того, данное рассуждение показывает независимость аксиомы (17) от предыдущих аксиом.

Утв. Доказать, что Доказательство. Предположим, что соотношение неверно. По аксиоме (6)Значит, по аксиоме (13)Пусть(т.е.– элемент, противоположный элементу 1 и существующий по аксиоме (3)). ТогдаПрибавим к обеим частям неравенствачисло(здесь мы используем аксиомы (14), (2), (4) и легко доказываемое утверждениеОтсюда(интересный результат:Умножим на(используя аксиому (15)):Докажем теперь вспомогательное утверждение о том, чтоДействительно, так кактот.е.Прибавим 1:Воспользуемся аксиомой (1):Ранее было доказано, чтоСледовательно,Мы получили противоречие с предположением. Утверждение доказано.