Взаимное положение прямых

Прямые могут располагаться параллельно, пересекаться или скрещиваться. Если прямые параллельны, то их одноименные проекции тоже параллельны (фронтальная с фронтальной и горизонтальная с горизонтальной). Если две прямые пересекаются, то их одноименные проекции тоже пересекаются, и проекции точки пересечения лежат на одной линии связи. Проекции скрещивающихся прямых могут пересекаться и не пересекаться в пределах видимости. Точки пересечения проекций не лежат на одной линии связи

Плоскость

Плоскость общего положениянаклонена к плоскостям проекций (рис.1.4). Ни на одну плоскость проекций она не проецируется в прямую линию.

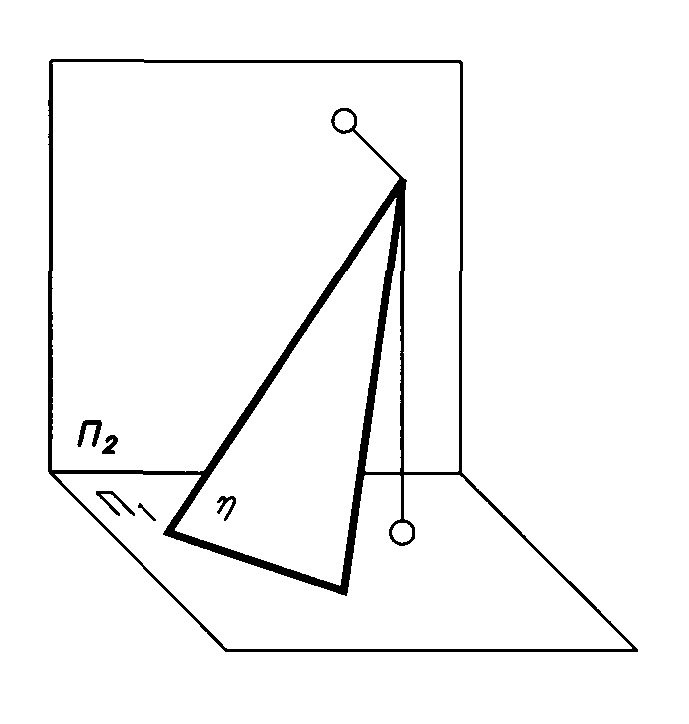
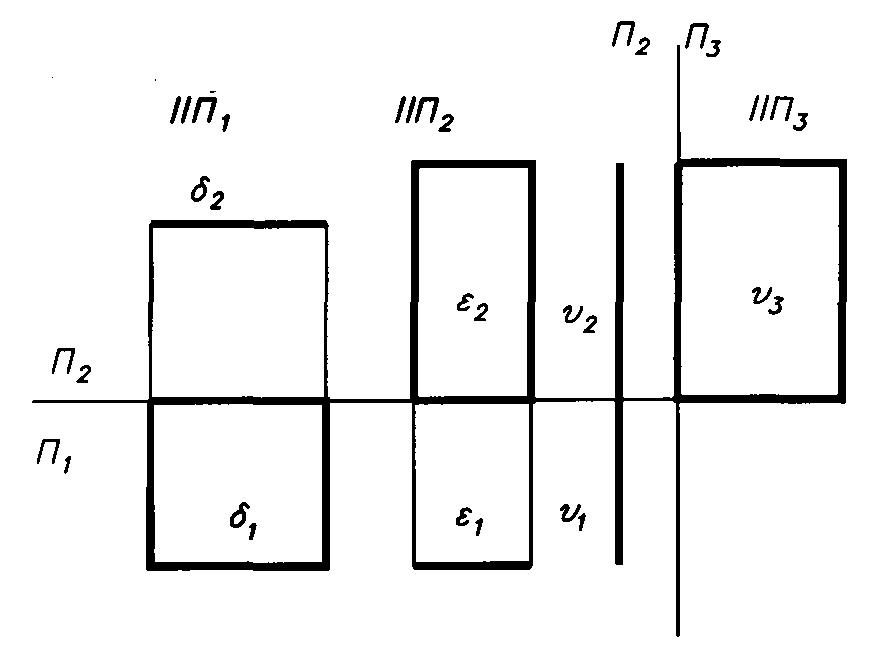
Рис.1.4. Рис.1.5.

Плоскости частного положенияпараллельны или перпендикулярны плоскостям проекций. На рис.1.5 показаны плоскости, параллельные одной из плоскостей проекций: – горизонтальная, – фронтальная,  – профильная(заданы прямоугольниками). Каждая плоскость проецируется на одну из плоскостей проекций в натуральную величину, другие же их проекции – прямые линии, перпендикулярны линиям связи.

Точка на поверхности вращения

Условимся точки обозначать прописными буквами латинского алфавита (A,B,C), их проекции на плоскости – прописными буквами с индексами (A₁,A₂,A₃,B₁,B₂,B₃,C₁,C₂,C₃), невидимые точки – в скобках ( (A₃), (B₂) ).

Точка, лежащая на проецирующем цилиндре (рис.1.6) проецируется на линию (окружность) – проекцию цилиндра, на нижнюю половину, если точка видима (точка А), и на верхнюю половину, если точка невидима (точкаВ, взятая в скобки на фронтальной проекции). На профильной проекции точкиА₃иВ₃находим с помощью координатy_Аиy_В, взятых относительно оси симметрии: А₃– справа от оси,В₃– слева (В₃– невидима (в скобках), поскольку находится на задней половине поверхности цилиндра).

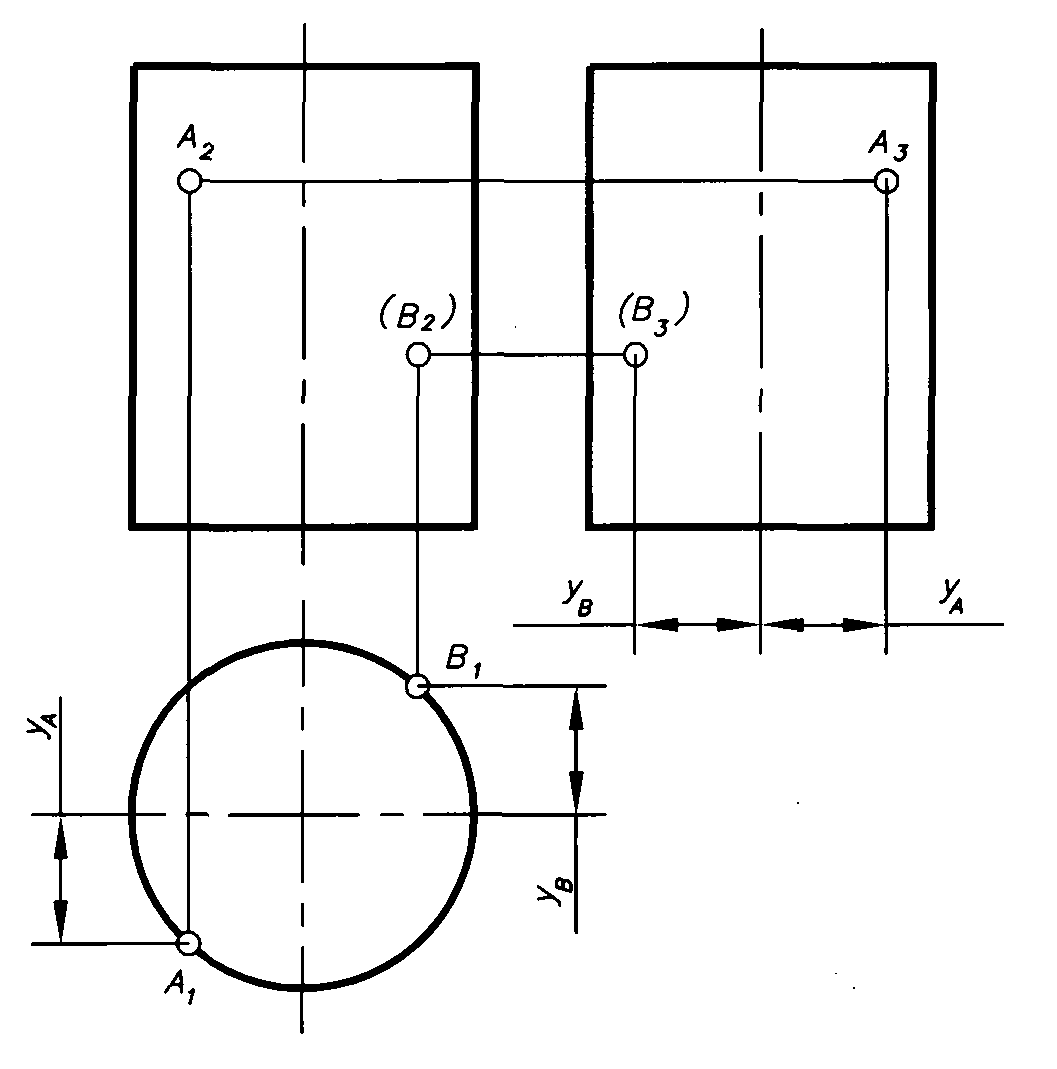
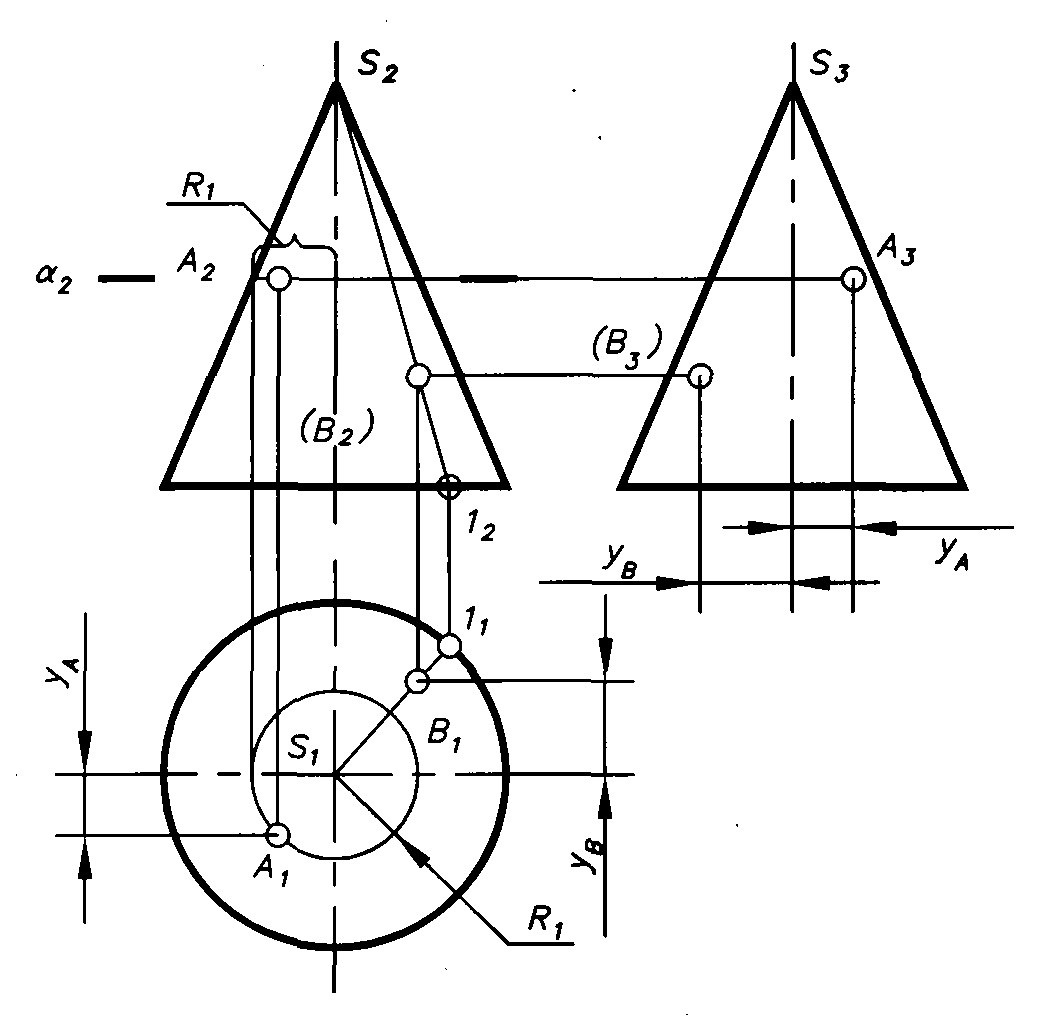
Рис.1.6. Рис.1.7.

Точки на поверхности конуса (рис.1.7) находим с помощью либо окружностина его поверхности, проходящей через заданную точкуА, либо с помощью прямой образующей, проходящей через точкуВ.

Окружность, проходящая через точку Аи расположенная в плоскости ,

перпендикулярной оси конуса, проецируется на фронтальную и

профильную проекции в виде прямой, а на горизонтальную проекцию в виде окружности с радиусом R₁. Поскольку точкаАна фронтальной проекции видима, на горизонтальной проекции она будет расположена в нижней части конуса. Профильная проекцияА₃ точки строится с помощью координатыy_А, расположенной справа от оси симметрии. Проекция точкиА₃– видима, т.к. расположена на передней поверхности конуса. Прямая образующая для построения точки находится с помощью точки1на основании конуса. Поскольку точкаВ₂на фронтальной проекции невидима (в скобках), прямая для ее построения должна быть расположена на горизонтальной проекции в верхней от оси симметрии части конуса. Профильная проекцияВ₃строится по двум ее проекциямВ₂иВ₁с помощью координатыy_В.

Т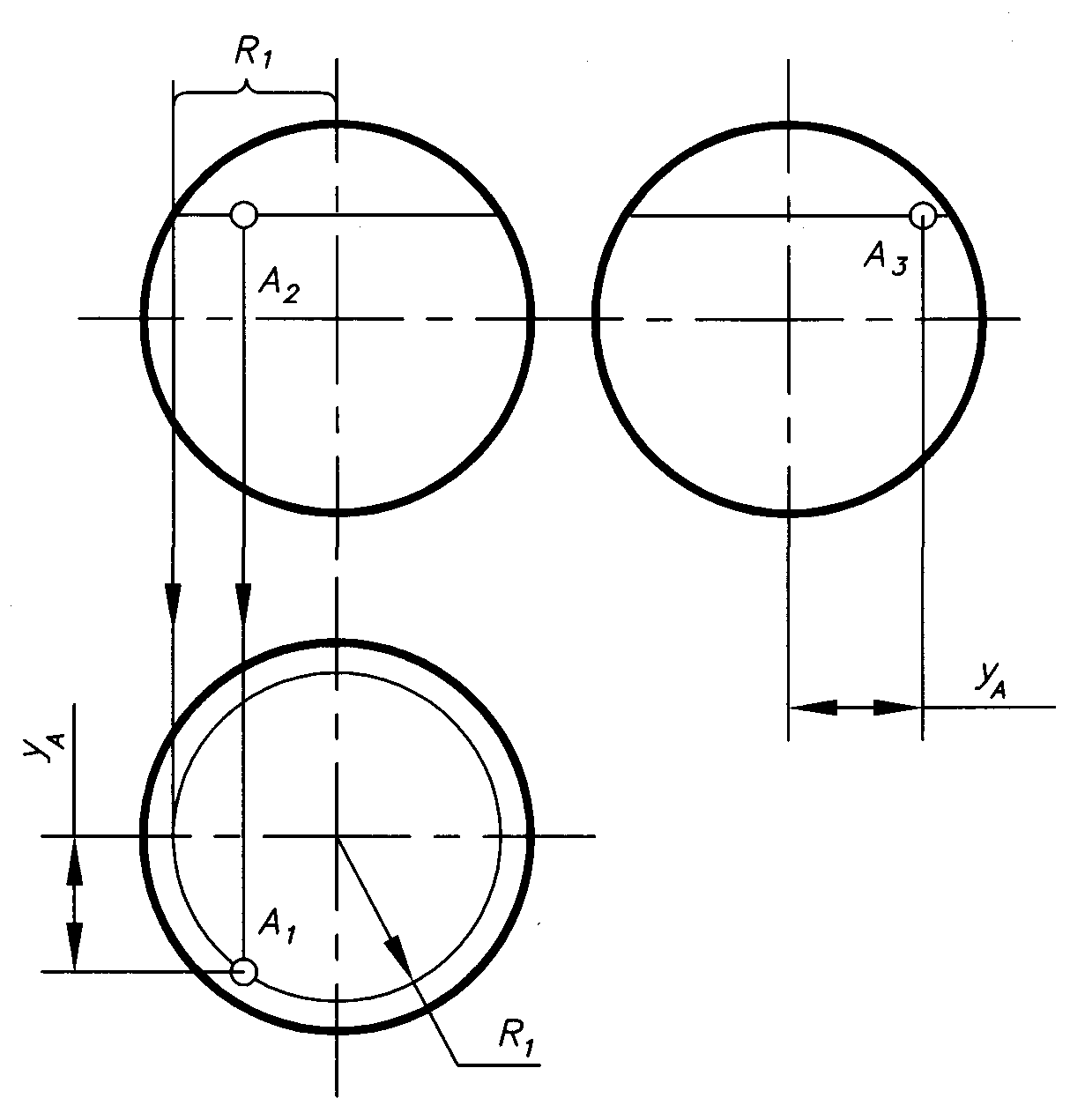очки на поверхности сферы (рис.1.8) строят с помощью окружностей, проходящих через заданные точки, расположенные перпендикулярно оси сферы (только в этом случае окружность на проекциях сферы проецируется в прямую или окружность, в противном случае она проецируется в виде эллипса!).

Рис.1.8.

Для определения проекции А₁точки строим на горизонтальной проекции окружность с радиусомR₁и получаем проекциюА₁на нижней половине горизонтальной проекции сферы (проекцияА₂точки – видима). Профильную проекциюА_3п построим, используя координатуy_А.

Точки на поверхности тора (рис.1.9) строят также с помощью вспомогательных окружностей (параллелей), проходящих через точки и расположенных в плоскостях, перпендикулярных оси вращения тора.

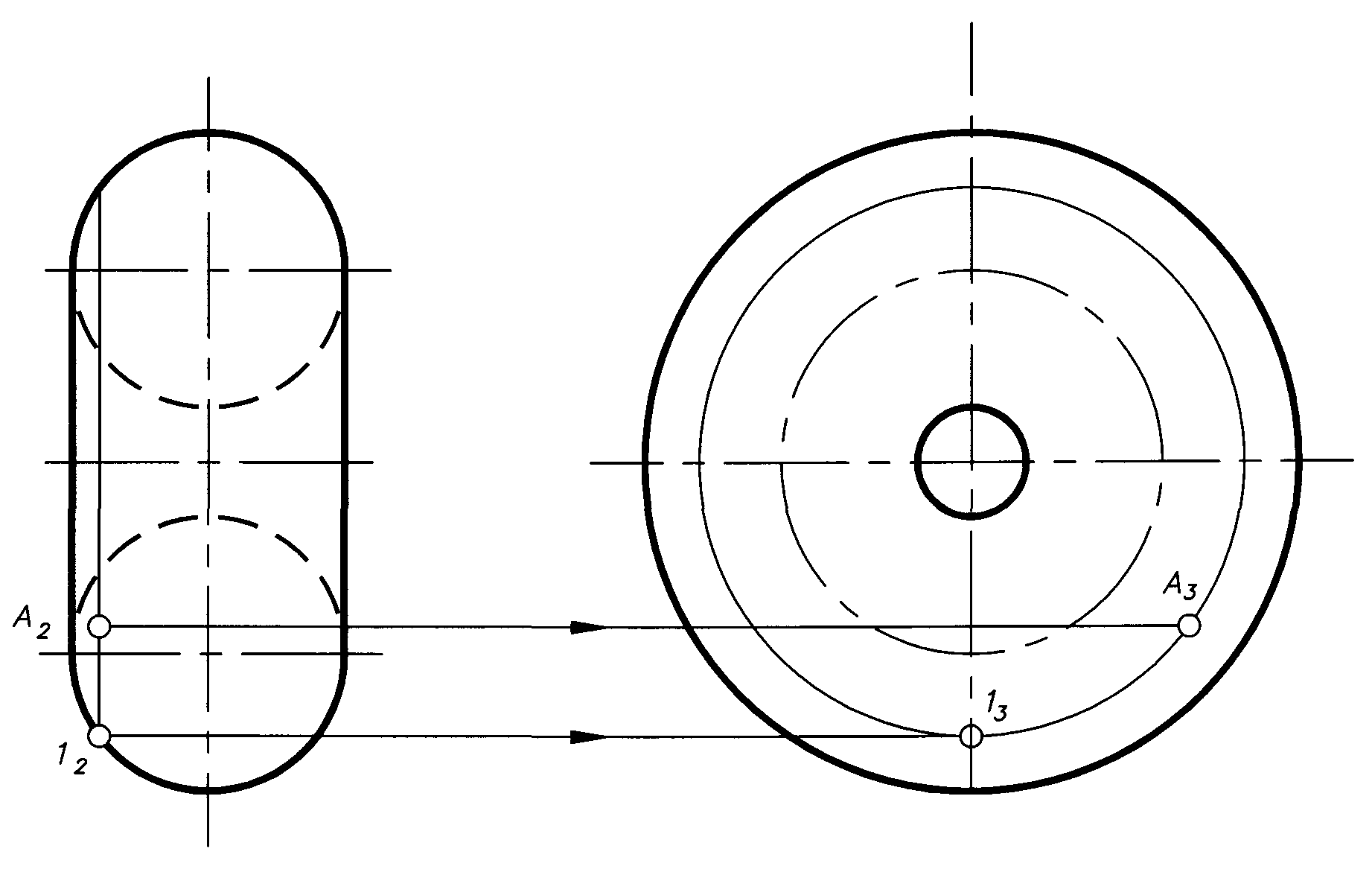
Рис.1.9

Окружность, например, проходящая через точку Аимеет одну проекцию – прямую, другую окружность. Зная одну проекцию точки на поверхности тора, напримерА₂, проводим через нее проекцию окружности, строим с помощью точки1(ее проекции – точки1₂и1₃) другую проекцию окружности (на фронтальной проекции – это прямая) и находим проекциюА₃. Она нанесена здесь при условии, что фронтальная проекцияА₂видима, т.е. точкаАлежит на ближней к нам части поверхности.