ФБТ БИ 2курс / протокол 1
.docxЛАБОРАТОРНА РОБОТА 1
ПОБУДОВА ГЛОБАЛЬНОГО ВИРІВНЮВАННЯ
Мета роботи – ознайомитись з поняттям глобального вирівнювання нуклеотидних й амінокислотних послідовностей, програмувати алгоритм глобального вирівнювання та використовувати програми глобального вирівнювання.
Теоретичні відомості
Темою даної лабораторної роботи є нова область математичного аналізу нуклеотидних послідовностей. Задача вирівнювання відноситься до класу задач біоінформатики, орієнтованих на пошук оптимальних алгоритмів для аналізу послідовностей.
Порівняння послідовностей необхідне для виявлення загальних структурних і функціональних особливостей та для дослідження еволюційних зв’язків. Задача вирішується тисячі разів на день молекулярними біологами та біотехнологами у всьому світі, тому потрібен оптимальний алгоритм з мінімальним часом вирівнювання.
Вирівнювання засновані на оптимізації явної функції премій за збіги й штрафів за розбіжності, що також називається "вагою" вирівнювання. Такі вирівнювання називаються вирівнюваннями, заснованими на подібності (вирівнювання, засновані на метричних відстанях мають менш загальний характер). Глобальне вирівнювання становить інтерес при дослідженні еволюції білків, наприклад, цитохромів С, гемоглобіну та ін.
Приклад вирівнювання. Розглянемо дві послідовності: AGTCTAGTCA й AGCTAGACA. Вони досить схожі, що стає очевидним, коли ми записуємо послідовності одну над іншою:
AGTCTAGTCA
(1)
AG*CTAGACA
Розходження пов'язані із зайвим Т у третій позиції та заміною Т на А у восьмій позиції зліва направо. Помітивши це, ми ввели пробіл в другій послідовності, щоб вирівняти співпадаючі основи ліворуч і праворуч від пробілу.
Для початку уточнимо, що мається на увазі під "вирівнюванням". Послідовності можуть відрізнятися за розміром. Як було показано вище, послідовності можуть містити пробіли. Ми визначимо вирівнювання як введення пробілів у довільних місцях послідовності так, щоб вони збіглися за розміром. Послідовності однакової довжини ми можемо записати тепер одну над іншою так, щоб установити відповідність між пробілами - символами однієї послідовності й пробілами - символами іншої. Після процедури вирівнювання кожному вирівнюванню можна привласнити вагу. Стовпчик вирівнювання одержує, залежно від змісту, певний бал, і загальна вага вирівнювання буде сумою балів по стовпчиках. Якщо два символи в стовпчику збігаються, то бал дорівнює 1 (збіг). У випадку розбіжності бал дорівнює –1, а пробіл у стовпчику означає бал –2. Найкращим вирівнюванням буде те, що максимізує загальну вагу вирівнювання. Цю максимальну вагу будемо називати подібністю двох послідовностей s, t і позначимо a(m,n), де m та n – кількість символів в послідовностях s та t. У загальному випадку може бути декілька вирівнювань з максимальною вагою.
Як приклад розрахуємо вагу вирівнювання (1). У нас є 8 стовпчиків з однаковими символами, один - з різними, і один символ-пробіл. Тоді сумарна вага буде
8*1+1*(-1)+1*(-2)=5
Чому були обрані величини -1, -2, 1? Вони досить часто використовуються на практиці, коли штрафуються пробіли й розбіжності.
Таким чином, природний підхід для з'ясування подібності між двома послідовностями полягає в побудові всіх можливих вирівнювань та виборі найкращого - тобто з максимальною вагою.
Число можливих вирівнювань. Існує теорема, доведена Лак’є: нехай f (n, m) - кількість всіх можливих вирівнювань послідовностей довжин n і m. Тоді для досить великихn справедливе співвідношення
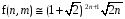 (2)
(2)
Тобто
для
двох послідовностей довжиною 1000
існує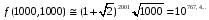 можливих
вирівнювань,
для прикладу
кількість елементарних
часток у Всесвіті порядку 1080,
число Авогадро
~1023.
можливих
вирівнювань,
для прикладу
кількість елементарних
часток у Всесвіті порядку 1080,
число Авогадро
~1023.
Таким чином, ми бачимо, що прямий перебір всіх вирівнювань неможливий.
Опис алгоритму
Існуючі підходи до вирівнювання засновані на техніці динамічного програмування. Основна ідея полягає в одержанні розв’язку "рекурентним" способом, тобто розв’язок задачі будується на основі вже отриманого розв’язку для об'єкта меншого розміру. Для двох послідовностей s і t замість того, щоб шукати вирівнювання (s, t) цілком, ми шукаємо вирівнювання між всіма можливими префіксами (s, t). Ми починаємо вирівнювання з короткими префіксами й використовуємо для більш довгих результати, отримані раніше.
Нехай m – довжина послідовності s і n – довжина послідовності t. В масив s1 заносимо послідовність з m символів, в масив s2 заносимо послідовність з n символів. Можна представити обчислення як масив a(i,j) розміру (m+l)*(n+l), де в позиції (i, j) зазначена подібність між префіксами s1[1..i] і s2[1..j].
На рис. 1.1 показано масиви ваг, що відповідають
s1[1…10] =TACGGTTGGG й s2[1…9] = TTGACAGTG (фрагмент ДНК E.coli). Відзначимо, що перший рядок і перший стовпчик ініціюються сумою добутку штрафів (за розбіжності у цьому випадку –2). Це відбувається тому, що якщо один рядок порожній, то можливе тільки одне вирівнювання: додається кількість пробілів, яка дорівнює довжині не порожнього рядка (k). Вага цього вирівнювання w(k)=g·k, де g = –2.
Тепер розглянемо інші можливості. Ключовий момент у тому, що ми можемо порахувати значення a(i,j), розглянувши всього три попередні значення: a(i-1, j), a(i-1, j-1) і a(i, j-1). Це пов'язане з тим, що s1 [l..i] й s2 [l..j] можна вирівняти тільки трьома способами, і кожний використовує одне з попередніх значень. Фактично, щоб одержати це вирівнювання, ми вибираємо з наступних трьох можливих варіантів:
1) вирівняти s1 [l..i] й s2 [l..j-l] і зіставити s2 [j] та пробіл;
2) вирівняти s1 [l..i-l] й s2 [l..j-l] і зіставити s1 [i] та s2 [j];
3) вирівняти s1 [l..i-l] й s2 [l..j] і зіставити s1 [i] та пробіл.
Ці можливості вичерпують вибір, оскільки ми не можемо вирівнювати пробіли в останньому стовбці вирівнювання. Ваги для вирівнювань префіксів меншого розміру вже містяться в масиві, якщо вибрано правильний порядок обчислень. Тому подібність може бути визначена наступною формулою:

a(i,j) = max {a(i,j-1)+g, a(i-1,j-1)+p(i,j), a(i-1,j)+g}, де
p(i,j) = + 1, s1, s1[j]=s2[j]
p(i,j) = - 1, vect_[i]≠s2[j]
|
p(i,j) |
|
T |
T |
G |
A |
C |
A |
G |
T |
G |
|
|
0 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
|
T |
-2 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
1 |
-1 |
|
A |
-2 |
-1 |
-1 |
-1 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
|
C |
-2 |
-1 |
-1 |
-1 |
-1 |
1 |
-1 |
-1 |
-1 |
-1 |
|
G |
-2 |
-1 |
-1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
1 |
|
G |
-2 |
-1 |
-1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
1 |
|
T |
-2 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
1 |
-1 |
|
T |
-2 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
1 |
-1 |
|
G |
-2 |
-1 |
-1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
1 |
|
G |
-2 |
-1 |
-1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
1 |
|
G |
-2 |
-1 |
-1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a(i,j) |
|
T |
T |
G |
A |
C |
A |
G |
T |
G |
|
|
0 |
-2 |
-4 |
-6 |
-8 |
-10 |
-12 |
-14 |
-16 |
-18 |
|
T |
-2 |
1 |
-1 |
-3 |
-5 |
-7 |
-9 |
-11 |
-13 |
-15 |
|
A |
-4 |
-1 |
0 |
-2 |
-2 |
-4 |
-6 |
-8 |
-10 |
-12 |
|
C |
-6 |
-3 |
-2 |
-1 |
-3 |
-1 |
-3 |
-5 |
-7 |
-9 |
|
G |
-8 |
-5 |
-4 |
-1 |
-2 |
-3 |
-2 |
-2 |
-4 |
-6 |
|
G |
-10 |
-7 |
-6 |
-3 |
-2 |
-3 |
-4 |
-1 |
-3 |
-3 |
|
T |
-12 |
-9 |
-6 |
-5 |
-4 |
-3 |
-4 |
-3 |
0 |
-2 |
|
T |
-14 |
-11 |
-8 |
-7 |
-6 |
-5 |
-4 |
-5 |
-2 |
-1 |
|
G |
-16 |
-13 |
-10 |
-7 |
-8 |
-7 |
-6 |
-3 |
-4 |
-1 |
|
G |
-18 |
-15 |
-12 |
-9 |
-8 |
-9 |
-8 |
-5 |
-4 |
-3 |
Рис.1. Двовимірні масиви ваг i-го та j-го елементів масивів vect_i та vect_j p(i,j) та ваг вирівнювань префіксів vect_i [1…i], vect_j [1…j] a(i,j).
Масив можна заповнювати порядково, зліва направо або по стовпчиках зверху вниз, це не має значення. Значення, наприклад, для а[1,2] вибирається як максимальне із трьох можливих: а[1, 1]-2=-1, а[0, 1]-1=-3 й а[0, 2]-2=-4.
Таким чином, є тільки один спосіб, яким можна одержати максимальне значення. Тепер зрозуміло як порахувати подібність між двома послідовностями.
Глобальне вирівнювання.
Одночасно з розрахунком матриці ваг ми будемо розраховувати ще й матрицю шляхів. Ця матриця буде містити одне з трьох значень, що буде відповідати положенню комірки, з якої було отримане максимальне значення.
Тоді, коли ми розрахуємо всю матрицю вирогідності, також отримаємо повну карту шляхів, якими ми рухались. Тепер, якщо відштовхуватись від останнього елементу матриці шляхів, можна планомірно прийти до першого елементу, заповнюючи при цьому результуючі вирівняні послідовності.
Складність алгоритму:
Створення матриць ваг та шляхів буде зі складністю O(n∙m), заповнення матриці ваг початковими значеннями буде займати O(n) та O(m) операцій.
Розрахункова частина алгоритму займає O(n∙m). Зворотній хід – від O(min(n,m)) до O(max(n,m)).
Тобто загальна складність буде O(n∙m).
Реалізація алгоритму
s1 = input("First sequence: ")
s2 = input("Second sequence: ")
s1 = "_" + s1
s2 = "_" + s2
p = []
way = []
for i in s1:
stolbik = []
wayStolbik = []
for j in s2:
stolbik.append(0)
wayStolbik.append("")
p.append(stolbik)
way.append(wayStolbik)
for i in range(len(s1)):
p[i][0] = -2 * i
for j in range(len(s2)):
p[0][j] = -2 * j
for x in range(1, len(s1)):
for y in range(1, len(s2)):
left = p[x-1][y] - 2
up = p[x][y-1] - 2
if (s1[x] == s2[y]):
slog = 1
else:
slog = -1
diag = p[x-1][y-1] + slog
p[x][y] = max(left, up, diag)
if (p[x][y] == left):
way[x][y] = "l"
if (p[x][y] == up):
way[x][y] = "u"
if (p[x][y] == diag):
way[x][y] = "d"
res1 = ""
res2 = ""
x = len(s1)-1
y = len(s2)-1
while (way[x][y] != ""):
if (way[x][y] == "d"):
res1 = s1[x] + res1
res2 = s2[y] + res2
x = x - 1
y = y - 1
if (way[x][y] == "u"):
res1 = "_" + res1
res2 = s2[y] + res2
y = y - 1
if (way[x][y] == "l"):
res1 = s1[x] + res1
res2 = "_" + res2
x = x - 1
while x:
res1 = s1[x]+res1
res2 = " " + res1
x = x - 1
while y:
res1 = " " + res1
res2 = s2[y] + res2
y = y - 1
print("P matrix:")
for s in p:
print(s)
print("Resulting sequence 1: " + res1)
print("Resulting sequence 2: " + res2)
Обладнання
Комп’ютер з встановленим Python та текстовим редактором.
Порядок виконання роботи
-
Ознайомитися з методом глобального вирівнювання.
-
Написати програму для реалізації алгоритму глобального вирівнювання.
-
Провести вирівнювання тестового прикладу послідовності відповідно до варіанту без допомоги програми.
-
Перевірити правильність ручних розрахунків за допомогою програми.