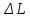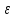- •Курсовая работа
- •«Анализ и синтез линейной непрерывной системы автоматического управления по требуемым показателям качества»
- •Москва 2014 Содержание
- •Функциональная схема системы управления и описание принципа ее работы в устройствах полиграфического производства.
- •Система управления температурой жидкости.
- •Частотный критерий устойчивости Найквиста.
Частотный критерий устойчивости Найквиста.
Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике разомкнутой системы.
Для статических систем управления этот критерия формулируется следующим образом:
-если разомкнутая система неустойчива
и имеет l правых
корней, то для устойчивости замкнутой
системы необходимо и достаточно, чтобы
амплитудно-фазовая характеристика
разомкнутой системыW(j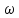 )
при изменении частоты
)
при изменении частоты от
0 до
от
0 до охватывала точку (-1,j0)
комплексной плоскости в положительном
направленииl/2раз;
охватывала точку (-1,j0)
комплексной плоскости в положительном
направленииl/2раз;
-если разомкнутая система устойчива, то замкнутая система устойчива при условии, что амплитудно-фазовая характеристика разомкнутой системы не охватывает точки (-1, j0).
В состав астатических систем разомкнутых систем входят интегрирующие звенья, поэтому комплексный коэффициент передачи:

обращается в бесконечность при
 = 0. Для оценки устойчивости таких систем
необходимо амплитудно-фазовую
характеристику разомкнутой системы
дополнить дугой, охватывающейv
квадрантов окружности бесконечного
радиуса, а затем применить к получившейся
кривой Найквиста.[2]
= 0. Для оценки устойчивости таких систем
необходимо амплитудно-фазовую
характеристику разомкнутой системы
дополнить дугой, охватывающейv
квадрантов окружности бесконечного
радиуса, а затем применить к получившейся
кривой Найквиста.[2]

Таблица 3.1. Таблица оценки устойчивости по критерию Найквиста.
![]()
![]()
![]()
![]()
![]()
Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системыпо амплитудно-фазовой частотной характеристике разомкнутой системы.
![]()

![]()


![]()

рис.3.2.Годограф Найквиста исходной системы управления.
Замкнутая система не устойчива, так как разомкнутая системана границе устойчивостиине имеетправых корнейl=0. Годограф Найквистаохватываетточку(-1, j0).
Расчет и построение асимптотических частотных характеристик и обоснование неустойчивости исходной системы (или недостаточности запасов устойчивости).
Комплексный коэффициент передачи сложной системы может быть представлен в виде произведения:

где Wi(j )
– комплексные коэффициенты передачи
элементарных звеньев.
)
– комплексные коэффициенты передачи
элементарных звеньев.
Для амплитудных и фазовых частотных характеристик имеем
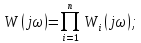
 .
.
Логарифмируя формулу, получим
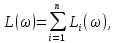
где


Из этих формул следует, что логарифмические фазовые и амплитудные частотные характеристики сложных систем получают суммированием соответствующих характеристик элементарных звеньев. [2]
Логарифмические характеристики строят в логарифмическом масштабе.
По оси абсцисс этого бланка частоту
 откладывают, как
откладывают, как ,
а оцифровывают в натуральных значениях
,
а оцифровывают в натуральных значениях .
.
Функция
 называется логарифмической
амплитудно-частотной характеристикой
(ЛАЧХ). По оси абсцисс откладывается
называется логарифмической
амплитудно-частотной характеристикой
(ЛАЧХ). По оси абсцисс откладывается ,
а по оси ординат
,
а по оси ординат .
Единица измерения
.
Единица измерения - децибел, а единица измерения интервала
частоты – декада. Декада – интервал
частоты, на котором она изменяется в
десять раз.
- децибел, а единица измерения интервала
частоты – декада. Декада – интервал
частоты, на котором она изменяется в
десять раз.
Единица в десять раз меньшая называется децибелом. ЛАЧХ всегда строятся для разомкнутой системы управления.
Передаточная функция разомкнутой части
исходной системы содержит интегрирующее
звено, то ЛАЧХ этого звена строится в
первую очередь и должна проходить через
точку с координатами
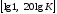 .
.
![]()
![]()
![]()
![]()
Используя методику, построим ЛАЧХ для следующей исходной системы:
![]()
![]()
![]()
 (астатизм 1-го порядка). Асимптота ЛАЧХ,
идущая под наклоном -20дБ/дек,
интегрирующего звена строится до
следующей частоты сопряжения.
(астатизм 1-го порядка). Асимптота ЛАЧХ,
идущая под наклоном -20дБ/дек,
интегрирующего звена строится до
следующей частоты сопряжения.
- апериодическое звено 1-го порядка с
частотой сопряжения
 и ее логарифмомlg20 =0.223имеет наклон ЛАЧХ
и ее логарифмомlg20 =0.223имеет наклон ЛАЧХ
- апериодическое звено 1-го порядка
с частотой сопряжения
 и ее логарифмомlg0.5
= -0.301 имеет наклон
ЛАЧХ
и ее логарифмомlg0.5
= -0.301 имеет наклон
ЛАЧХ
Помимо получения асимптотической ЛАЧХ исходной системы управления методом построения асимптот отдельных элементарных звеньев, можно рассчитать уравнения каждой из асимптот.
Для интегрирующего звена формула ЛАЧХ:

![]()
![]()
![]()
![]()

График ЛАЧХ исследуемой системы:
![]()

Рис. 4.1. ЛАЧХ исходной системы управления.
При построении ЛФЧХ системы производится
суммирование ЛФЧХ отдельных звеньев в
соответствии с формулой
 .
Наличиеnинтегрирующих
учитывается опусканием характеристики
наn
.
Наличиеnинтегрирующих
учитывается опусканием характеристики
наn .
.
Для построения ЛФЧХ необходимо учесть изменение масштаба по шкале частот. На частоте ω=ω(сопр), ψ(ω(сопр))= -π/4. [1]
Фазовая частотная характеристика.
![]()
интегрирующее звено ψ = -π/2![]()
![]()
![]()
апериодическое звено 1го порядка 0 <
ψ << -π/2
апериодическое звено 1го порядка 0 <
ψ<< -π/2![]()
![]()
![]()
![]()
![]()
![]()

Обоснование неустойчивости исходной системы:
По исследуемым графикам ЛАЧХ и ЛФЧХ
исходной системы видно, что частота
среза
 и
частота
и
частота 1.
Отсюда следует, что система
неустойчива, так как
1.
Отсюда следует, что система
неустойчива, так как и
не имеет смысла говорить о запасах
устойчивости.
и
не имеет смысла говорить о запасах
устойчивости.
Коррекция (последовательная) системы управления по требуемым показателям качества, определение передаточной функции корректирующей системы, построение её ЛАЧХ и ЛФЧХ.
Определение передаточной функции скорректированной системы.
Коррекция – выбор устройства, улучшающего качество работы системы.
Желаемой называют логарифмическую амплитудно-частотную характеристику, имеющую требуемые статические и динамические свойства. Она состоит из трех основных асимптот: низкочастотной, среднечастотной и высокочастотной.
Низкочастотная определяет статические свойства системы, среднечастотная – устойчивость и показатели качества, высокочастотная мало влияет на свойства системы.
При построении желаемой логарифмической амплитудно-частотной характеристики исходными данными являются:
-коэффициент усиления системы;
-порядок астатизма;
-время регулирования;
-перерегулирование.
Существует несколько методик построения желаемых характеристик. Все они основаны на использовании специальных номограмм и приближенных формул.
Построение желаемой характеристики для исходной системы:
![]()
а необходимые показатели качества
переходного процесса: перерегулирование
 ,
время регулирования
,
время регулирования .
.
Для построения желаемой характеристики
воспользуемся номограммами. При σmax=35% наибольшее значение
вещественной частотной характеристики
будетPmax=
1.38. ПоPmax
находим время регулированияtр
=4.8П/ωπ , где ωπ - частота положительной
желаемой вещественной частотной
характеристики Р(ω), изображенной на
рисунке. [2]
, где ωπ - частота положительной
желаемой вещественной частотной
характеристики Р(ω), изображенной на
рисунке. [2]
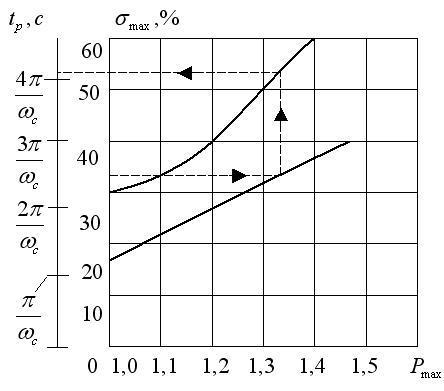

Рис.5.1. Номограммы Солодовникова.
Подставляя сюда tр =4.8П/ωπ заданноеtр =7,
находим ωπ =2.15рад/с. По формулеtр =4.5П/ωс
заданноеtр =7,
находим ωπ =2.15рад/с. По формулеtр =4.5П/ωс находим ωс =2.01.
находим ωс =2.01.
Желаемый коэффициент передачи: 20lg(Kжел) =2.5, отсюда находимKжел=102.5/20=1.3
Передаточная функция разомкнутой скорректированной системы управления:
![]()
Замкнутая система управления:
![]()
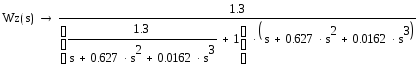
![]()
Наиболее распространено применение последовательных корректирующих устройств.
Методика выбора корректирующего устройства включает в себя следующие этапы:
- построение нескорректированной и желаемой амплитудно-частотных характеристик;
- определение логарифмической амплитудно-частотной характеристики корректирующего звена вычитанием из характеристики нескорректированной системы желаемой характеристики;
- определение передаточной функции и схемы корректирующего звена.
Определение передаточную функцию корректирующей системы управления. [2]
![]()
![]()
![]()
![]()
Построение ЛАЧХ и ЛФЧХ корректирующей системы:
![]()
![]()
![]()
![]()
Логарифмическая амплитудно-частотная характеристика.
Используя методику, построим ЛАЧХ для следующей корректирующей системы:
![]()
- форсирующее звено 1-го порядка с
постоянной времени![]()
 частотой сопряжения
частотой сопряжения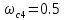 ,
, предельный наклон ЛАЧХ
предельный наклон ЛАЧХ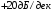
3.
![]()
- апериодическое звено 1-го порядка с
частотой сопряжения
 37
и ее логарифмомlg37= 1.568имеет наклон ЛАЧХ
37
и ее логарифмомlg37= 1.568имеет наклон ЛАЧХ
Помимо получения асимптотической ЛАЧХ корректирующей системы управления методом построения асимптот отдельных элементарных звеньев, можно рассчитать уравнения каждой из асимптот.
![]()
![]()
![]()

![]()
![]()

Фазовая частотная характеристика.
![]()
![]()
![]()
форсирующее звено 0 < ψ<< π/2
апериодическое звено 1го порядка 0 < ψ << -π/2
![]()
![]()
![]()
![]()
![]()

Рис.5.3. Фазовая частотная характеристика корректирующей системы.
Оценка запасов устойчивости скорректированной системы управления по ЛАЧХ и ЛФЧХ.
Логарифмическая амплитудно-частотная характеристика.
![]()
![]()
![]()
![]()
Построим ЛАЧХ для следующей скорректированной системы:
![]()
![]()
 (астатизм 1-го порядка). Асимптота ЛАЧХ,
идущая под наклоном -20дБ/дек,
интегрирующего звена строится до
следующей частоты сопряжения.
(астатизм 1-го порядка). Асимптота ЛАЧХ,
идущая под наклоном -20дБ/дек,
интегрирующего звена строится до
следующей частоты сопряжения.
- апериодическое звено 1-го порядка
с частотой сопряжения и ее логарифмомlg37= 1.568имеет наклон ЛАЧХ
и ее логарифмомlg37= 1.568имеет наклон ЛАЧХ
4.
![]()
 и ее логарифмомlg1.6= 0.204имеет наклон ЛАЧХ
и ее логарифмомlg1.6= 0.204имеет наклон ЛАЧХ![]()
Помимо получения асимптотической ЛАЧХ скорректированной системы управления методом построения асимптот отдельных элементарных звеньев, можно рассчитать уравнения каждой из асимптот.
Для интегрирующего звена формула ЛАЧХ:
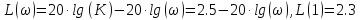
![]()
![]()
![]()
![]()

График ЛАЧХ исследуемой скорректированной системы:
![]()

Фазовая частотная характеристика.
апериодическое звено 1го порядка 0 <
ψ << -π/2
апериодическое звено 1го порядка 0 <
ψ << -π/2
![]()
![]()
![]()
интегрирующее звено ψ = -π/2![]()
![]()
![]()
![]()
![]()
![]()
![]()

Оценка запасов устойчивости:
Запасы устойчивости удобно определять
с использованием логарифмических
частотных характеристик разомкнутых
систем. Запас устойчивости по фазе
отсчитывается на частоте среза
 ,
а запас устойчивости по амплитуде (по
модулю) находитсяпри
частоте
,
а запас устойчивости по амплитуде (по
модулю) находитсяпри
частоте .
.
По исследуемым графикам ЛАЧХ и ЛФЧХ
скорректированной системы видно, что
частота среза
 и
частота
и
частота .
Отсюда следует, что система устойчива,
так как
.
Отсюда следует, что система устойчива,
так как .
Также запас устойчивости по амплитуде
.
Также запас устойчивости по амплитуде ,
а запас устойчивости по фазе
,
а запас устойчивости по фазе .
.
Оценка устойчивости скорректированной замкнутой системы управления.
Алгебраический критерий устойчивости Гурвица:
Определим передаточную функцию замкнутой скорректированной системы:
Передаточная функция замкнутой
скорректированной системы:
![]()
![]()

![]()
Критерий Гурвица позволяет судить об
устойчивости системы на основании
анализа коэффициентов характеристического
уравнения
Для нахождения достаточных условий
устойчивости коэффициентов
характеристического уравнения составляем
определитель Гурвица.![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
Система устойчива, так как Δ3, Δ2, Δ1
больше нуля
Частотный критерий устойчивости Михайлова:
Характеристический многочлен
Частотный критерий устойчивости
Михайлова основан на использовании
характеристического вектора
![]()
![]()
![]()
![]()
Для устойчивости системы необходимо,
чтобы годограф Михайлова, начинался
на положительной вещественной полуоси,
не нарушая последовательности обхода
квадрантов координатной плоскости
(против часовой стрелки), нигде не
обращаясь в ноль и не пересекаясь сама
с собой.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Рис.8.1. Годограф Михайлова скорректированной системы.
Система устойчива, так как годограф Михайлова начинается на вещественной положительной полуоси, нигде не обращаясь в ноль и не пересекается сам с собой.
Частотный критерий устойчивости Найквиста.
Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике разомкнутой системы.
![]()
![]()
![]()
![]()
![]()
![]()

![]()


![]()

Рис.8.2. Годограф Найквиста скорректированной системы.
Замкнутая система устойчива, так как разомкнутая системана границе устойчивостиине имеетправых корнейl=0. Годограф Найквистане охватываетточку(-1, j0).
Оценка частотных показателей качества: резонансного пика, резонансной частоты и полосы пропускания.
Частотные показатели качества:
Резонансный пик– отношение максимального значения амплитудной частотной характеристики кначальному значению АЧХ W(0).
Резонансная частота, при которой амплитудная частотная характеристика принимаетмаксимальное значение, называетсярезонанснойчастотой.
Полоса пропускания – диапазон частот от0 до частоты, при которой амплитудная частотная характеристика принимает значение0,707 отначального W(0).
Передаточная функция замкнутой скорректированной САУ:
![]()
![]()
![]()
![]()
![]()

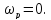 95
-резонансная частота;
95
-резонансная частота;
 -частота полосы
пропускания;
-частота полосы
пропускания;
![]() -
резонансный
пик.
-
резонансный
пик.
Оценка корневых показателей качества регулирования: быстродействия, степени устойчивости и степени колебательности скорректированной САР.
Степень устойчивости системы управления (характеристического полинома)η называют расстояние от мнимой оси до ближайшего корня его характеристического уравнения (все корни "левые").
Быстродействиесистемы (быстрота затухания переходного процесса) характеризуется еёстепенью устойчивости η=min(-Resi)=max Resi.
Степень колебательности (колебательность) системы управления (характеристического полинома)называют максимальный тангенс угла наклона между отрицательной вещественной полуосью и прямой и прямой, проведенной из начала координат к ближайшему левому корню, его характеристического уравнения (все корни левые).
Степень колебательности (колебательность) системы μ косвенно характеризуетколебательность системыμ=max tgϕ=max Imsi/Resi.
Передаточная функция замкнутой скорректированной системы:
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()


Степень устойчивости:
Степень колебательности:
![]()
![]()
Рис.10.1. Расположение полюсов системы на комплексной плоскости.
Оценка качества регулирования, расчет коэффициентов ошибок скорректированной системы управления и построение графика статической ошибки.
Коэффициенты ошибок позволяют находить вынужденную составляющую сигнала на выходе системы в установившемся режиме при наличии на входе медленно изменяющегося воздействия x(t).
Статической ошибкой ε называется установившаяся ошибка при постоянном внешнем воздействии. Передаточная функция ошибки ε(t)=x(t)-y(t) имеет вид Wε(s)=1/( 1+W(s)). [1]
Передаточная функция разомкнутой скорректированной системы:
![]()
Найдем установившуюся ошибку, если на входе имеется регулярное воздействие:
![]()
![]()
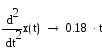

Передаточная функция ошибки будет:
![]()


Коэффициенты ошибок:
![]()
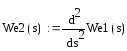

![]()
![]()
![]()
Вынужденная составляющая ошибки скорректированной системы будет:


![]()
Рис.11.1 График ошибки при воздействии x(t).
Статическая ошибка:
![]()

![]()
![]()
![]()
![]()

Рис.11.2. График статической ошибки.
Расчет и построение весовой и переходной характеристик скорректированной САР и оценка прямых показателей качества системы.
Качеством процесса управленияназывают совокупность требований,
определяющих поведение системы в
установившемся и переходном режимах
при наличии на входе различных воздействий.Прямые методы оценки качества систем
управленияоснованы на анализе
переходной или весовой функции. Основными
показателями качества являютсявремя
регулирования и перерегулирование. К
прямым оценкам качества относятся
также: время нарастания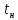 ,
время достижения первого максимума
,
время достижения первого максимума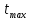 ,
частота и число колебаний, которые имеет
переходная функция за время регулирования,
и декремент затухания.
,
частота и число колебаний, которые имеет
переходная функция за время регулирования,
и декремент затухания.
Переходной функцией системы называют функцию, описывающую реакцию системы на единичное ступенчатое (ступенька) воздействие при нулевых начальных условиях. График называютразгонной характеристикой.
Импульсной переходной или весовой функцией (веса) называют функцию, описывающую реакцию наединичное импульсное (импульс)воздействие при нулевых начальных условиях.
Время регулирования
 -минимальный промежуток времени, по
истечении которого разница между
переходной функцией и ее установившимся
значением
-минимальный промежуток времени, по
истечении которого разница между
переходной функцией и ее установившимся
значением не превышает заданного значения
не превышает заданного значения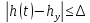 .
Значение
.
Значение обычно выбирается в пределах от 1-5 % от
величины
обычно выбирается в пределах от 1-5 % от
величины .
.
Перерегулирование
 -это относительная разность между
максимальным значением переходной
функции и установившимся значением,
выраженная в %.
-это относительная разность между
максимальным значением переходной
функции и установившимся значением,
выраженная в %.
Время нарастания – время достижения системой первый раз установившегося значения.
Переходная характеристика скорректированной системы:
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()

Переходный процесс данной системы имеет апериодический характер.
Установившееся значение переходной характеристики:
![]()
Верхняя и нижняя границы 5% коридора допустимого отклонения переходной характеристики от ее установившегося значения
![]()
По исследуемой переходной функции
скорректированной системы видно, что
время регулирования
 ,
,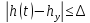 .
.
Перерегулирование:
![]()
![]() %
%
![]()
Время нарастания:
![]()
Время достижения первого максимума:
Весовая характеристика скорректированной системы.
![]()
![]()
![]()
![]()

Рис.12.2. Весовая характеристика скорректированной САР.
Выводы о качестве регулирования в скорректированной системе управления.
|
Показатели качества САР |
Требуемые |
Рассчитанные |
|
Запас
устойчивости по фазе,
|
40-50 |
52 |
|
Запас
устойчивости по амплитуде,
|
6-10Дб |
27Дб |
|
Время
регулирования,
|
7с |
3,7с |
|
Перерегулирование,
|
30-40 % |
13% |
|
Статическая
ошибка,
|
0 % |
0 % |
Таблица13.1. Требуемые и рассчитанные показатели качества.
Список использованной литературы:
М.В. Ефимов. Теория автоматического управления. Учебное пособие. Москва: МГУП, 2006г.
М.В, Ефимов, О.А. Винокурова, Ю.В. Щербина, А.Е.Иванова. Теория автоматического управлении. Линейные системы управления. Методические указания по курсовому проектированию. Москва: МГУП, 2004г.
http://www.findpatent.ru/patent/252/2527505.html.