Содержание

1 (107) Задача №107 2

2 (127) Задача №127 3

3 (147) Задача №147 5

4 (167) Задача №167 решение 7

5 (187) Задача №187 решение 8

6 (207) Задача №207 решение 11

1 (107) Задача №107

Найти интегралы:

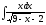а) б) ; в) .

Решение:

а)

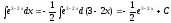
б)

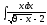
Сделаем замену ,

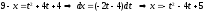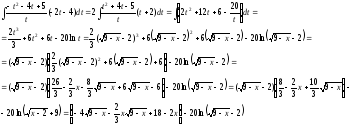
в)

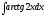
Интегрируем по частям по формуле: .

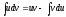И воспользуемся формулой

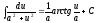
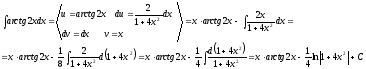
2 (127) Задача №127

Вычислить определенные интегралы:

а) 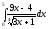; б) .

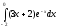а)

Cделаем подстановку. Пусть

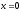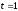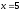Тогда Определим пределы интегрирования для переменной t. При получаем , при получаем .

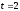Выразив подынтегральное выражение через t и переходя к новым пределам, получим

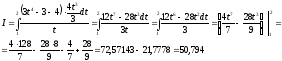
б) .

Интегрируем по частям по формуле: .

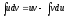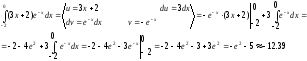
3 (147) Задача №147

Вычислить площадь фигуры, ограниченной линиями:

.

Решение:

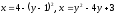
Изобразим на числовой оси данные фигуры. Перед этим поменяем местами оси координат. Графиками данных функций являются параболы.

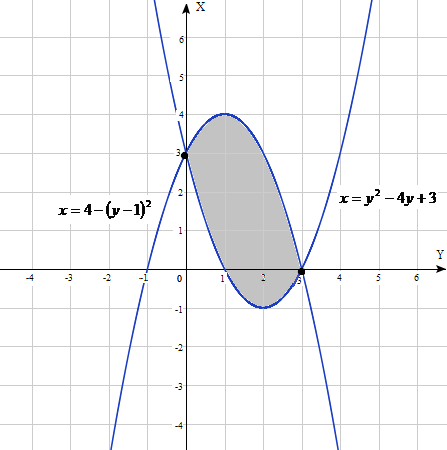
Для определения точек пересечения графиков функции, необходимо решить уравнение:

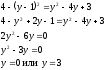
Значит, точки пересечения есть (0; 0), (3; 0).

Площадь кривой, заданной в декартовых координатах, определяется по формуле:

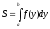. Где пределы интегрирования находятся как точки пересечения графиков, мы их нашли ранее, это 0 и 3.

Так график функции располагается выше графика функции 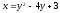, поэтому из верхнего графика вычитаем нижний.

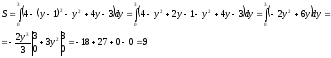
Ответ: S=9 кв.ед.

4 (167) Задача №167 решение

Дана функция 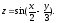Найти:

1) полный дифференциал dz;

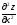
2) частные производные второго порядка и ;

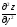3) смешанные частные производные и .

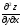Решение:

1) Составим полный дифференциал первого порядка:

.

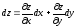Для этого найдем частные производные первого порядка 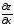и :

;

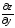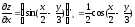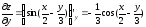
Тогда

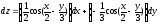
2) Находим частные производные второго порядка:

;

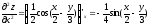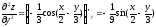
3) смешанные частные производные:

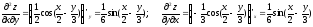
Как видно, смешанные производные равны между собой, т.е. удовлетворяется равенство:

.

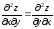5 (187) Задача №187 решение

Требуется: 1) построить на плоскости хОу область интегрирования заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования.

Решение:

1. Пределы внешнего интеграла по переменной х – числа 0 и 6 – указывают на то, что область D ограничена слева прямой х=0 и справа прямой х=6.

Пределы внутреннего интеграла по переменной у указывают на то, что область D ограничена снизу прямой и сверху прямой 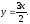Построив эти линии на отрезке [0; 6], получим область D:

2. Чтобы изменить порядок интегрирования, установим пределы интегрирования для внешнего интеграла по переменной у. Как видно из рисунка наименьшее значение, которое принимает у в области D, равно 0 в точке А(0;0), а наибольшее значение равно 9 в точке В(6;9). Следовательно, внешний интеграл по переменной у будет иметь пределы: 0 (нижний предел) и 9 (верхний предел).

Определим пределы для внутреннего интеграла по переменной х.

Из уравнения параболы получаем 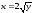верхний предел (верхний предел, потому что относительно оси Oy парабола будет находиться выше).

Из уравнения прямой получаем 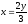– нижний предел (нижний предел, потому что относительно оси Oy прямая будет находиться ниже).

Таким образом, с учетом полученных пределов, интеграл примет вид:

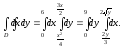
Вычислим площадь области D при заданном порядке интегрирования:

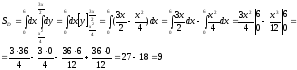
Интегрирование происходило по формуле .

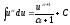Вычислим площадь области D при измененном порядке интегрирования:

Интегрирование происходило по формуле .

Как видно, значение интегралов совпадают как при заданном порядке интегрирования, так и при измененном порядке интегрирования. Соответственно, площадь равна

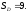
6 (207) Задача №207 решение

Исследовать сходимость ряда, пользуясь признаком сходимости Даламбера.

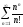
Решение:

Применяем признак Даламбера:

На основании признака Даламбера ряд сходится при 0<k<1 и расходится при k>1. Если k=1, то признак Даламбера ответа не дает, где k равно полученному значению предела. В нашем случае, 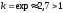, т.е. ряд расходится по признаку Даламбера.

11