
- •Содержание
- •Исходные данные
- •Определение средней многолетней величины годового стока при наличии данных наблюдений
- •Определение коэффициента изменчивостиCvгодового стока
- •Определение нормы стока при недостаточности данных наблюдений методом гидрологической аналогии
- •Построение аналитической кривой обеспеченности и проверка её точность с помощью эмпирической кривой обеспеченности
- •Выполнение внутригодового распределения стока по методу реального года
- •Список литературы
Определение средней многолетней величины годового стока при наличии данных наблюдений
Определим среднюю многолетнюю величину (норму) годового стока Река Колпь, пункт Верхний Двор по данным с 1969 по 1978 гг. (10 лет).
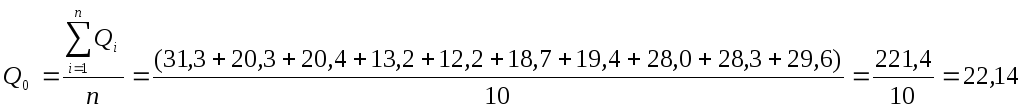 м3/с
м3/с
Полученную норму в виде среднего многолетнего расхода воды требуется выразить через другие характеристики стока: модуль, слой, объем и коэффициент стока.
Средний многолетний модуль стока вычислить по соотношению:
![]() л/с
км2
л/с
км2
где F – площадь водосбора, км2.
Объем стока – объем воды, стекающей с водосбора за какой-либо интервал времени.
Вычислим средний многолетний объем стока за год:
W0= Q0 хT = 22,14 .31,54.106 = 698,3 106 м3
где Т – число секунд в году, равное 31,54.106
Средний многолетний слой стока вычислим по зависимости:
![]() 220,98
мм/год
220,98
мм/год
Средний многолетний коэффициент стока
![]()
где х0- средняя многолетняя величина осадков в год
Оценка репрезентативности (достаточности) ряда наблюдений определяется величиной относительной среднеквадратической ошибки средней многолетней величины (нормы) годового стока, вычисляем по формуле:
![]()
где CV – коэффициент изменчивости (вариации) годового стока; длина ряда считается достаточной для определения Qo, если εQ≤10%. Величина среднего многолетнего стока при этом называется нормой стока.
Определение коэффициента изменчивостиCvгодового стока
Коэффициент изменчивости CV характеризует отклонения стока за отдельные годы от нормы стока; он равен:
![]()
где σQ – среднеквадратическое отклонение годовых расходов от нормы стока
![]()
Если
сток за отдельные годы выразить в виде
модульных коэффициентов
![]() коэффициент
вариации определяется по формуле
коэффициент
вариации определяется по формуле
![]()
Составляем таблицу для подсчета годового стока Река Колпь, пункт Верхний Двор (табл.1)
Таблица 1
Данные для подсчёта Сv
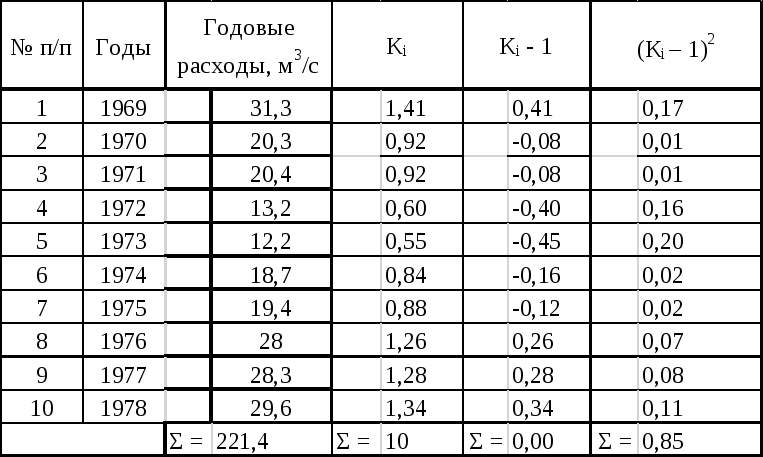
Определим коэффициент изменчивости Cv годового стока:
![]()
Относительная среднеквадратическая ошибка средней многолетней величины годового стока стока Река Колпь, пункт Верхний Двор за период с1969 г. по 1978 г. (10 лет) равна:
![]()
Относительная среднеквадратическая ошибка коэффициента изменчивости Сv при его определении методом моментов равна:
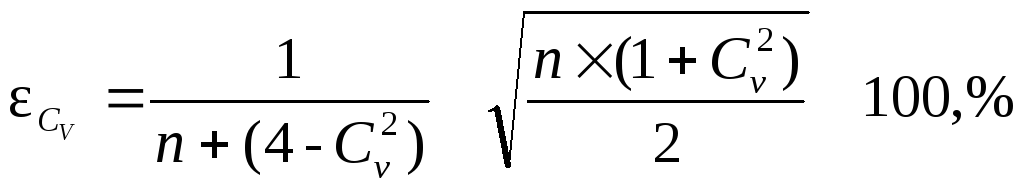
![]() .
.
Определение нормы стока при недостаточности данных наблюдений методом гидрологической аналогии
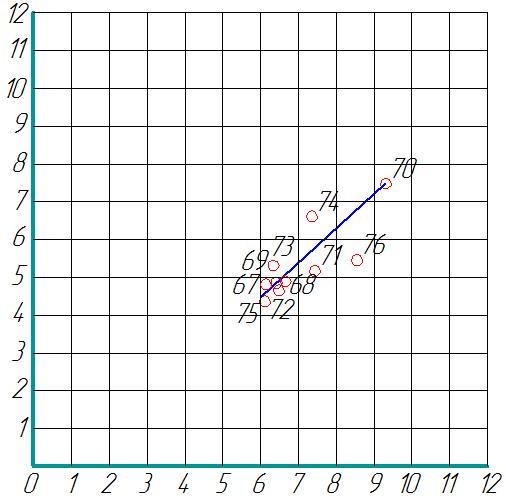
Рис.1 График связи среднегодовых модулей стока
изучаемого бассейна Река Колпь, пункт Верхний Двор и бассейна аналога р. Обнора, с. Шарна.
По графику связи среднегодовых модулей стока Река Колпь, пункт Верхний Двор и бассейна аналога р. Обнора, с. Шарна.М0=5,9 л/с км2 (снимается с графика по величине М0а=7,9 л/с км2)
![]()
Коэффициент изменчивости годового стока вычислить по формуле
![]()
Cv – коэффициент изменчивости стока в расчетном створе;
СVа – в створе реки-аналога;
Моа – среднемноголетняя величина годового стока реки- аналога;
А – тангенс угла наклона графика связи.
![]()
Окончательно для построения кривых принимаем Qo=18,64 м3/с, СV=0,336.
Построение аналитической кривой обеспеченности и проверка её точность с помощью эмпирической кривой обеспеченности
Коэффициент асимметрии Cs характеризует несимметричность гидрологического ряда и определяется путем подбора, исходя из условия наилучшего соответствия аналитической кривой с точками фактических наблюдений; для рек, расположенных в равнинных условиях, при расчете годового стока наилучшие результаты дает соотношение Cs = 2CV. Поэтому принимаем для Река Колпь, пункт Верхний Двор Cs=2СV=0,336 с последующей проверкой.
Ординаты кривой определяем в зависимости от коэффициента Cv по таблицам, составленным С Н. Крицким и М. Ф. Менкелем для CS = 2CV.
Таблица2
Ординаты аналитической кривой обеспеченности среднегодовых
расходов воды Река Колпь, пункт Верхний Двор

Обеспеченностью гидрологической величины называется вероятность превышения рассматриваемого значения гидрологической величины среди совокупности всех возможных ее значений.
Модульные коэффициенты годовых расходов расположим по убыванию (табл. 3) и для каждого из них вычислить его фактическую эмпирическую обеспеченность по формуле:
![]()
где m – порядковый номер члена ряда;
n – число членов ряда.
Pm1=1/(10+1) 100= 9,1 Pm2=2/(10+1)100= 18,2 и т.д.
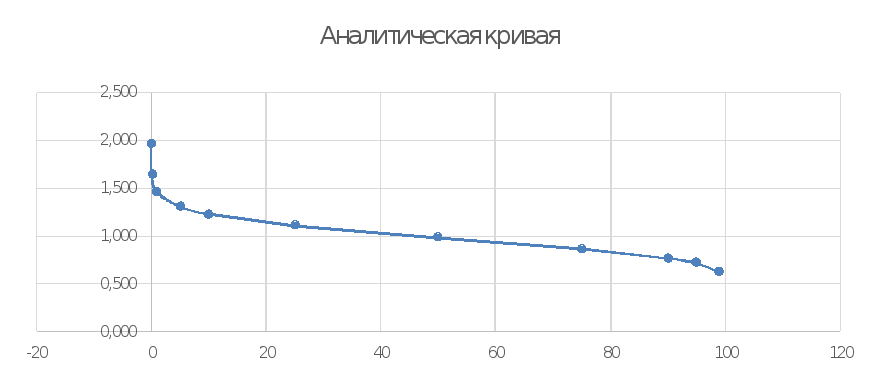
Рисунок – Аналитическая кривая обеспеченности
Нанося на график точки с координатами (Pm, Qm) и осредняя их на глаз, получим кривую обеспеченности рассматриваемой гидрологической характеристики.
Как видно, нанесенные точки лежат очень близко к аналитической кривой; из чего следует, что кривая построена правильно и соотношение CS = 2CV соответствует действительности.
Таблица 3
Данные для построения эмпирической кривой обеспеченности
Река Колпь, пункт Верхний Двор
|
№ п\п |
Модульные коэффициенты (Кi)по убыванию |
Фактическая
обеспеченность |
Годы соответствующие Кi |
|
1 |
1,41 |
9,1 |
1996 |
|
2 |
1,34 |
18,2 |
1978 |
|
3 |
1,28 |
27,3 |
1977 |
|
4 |
1,26 |
36,4 |
1976 |
|
5 |
0,92 |
45,5 |
1970 |
|
6 |
0,92 |
54,5 |
1971 |
|
7 |
0,88 |
63,6 |
1975 |
|
8 |
0,84 |
72,7 |
1974 |
|
9 |
0,60 |
81,8 |
1972 |
|
10 |
0,55 |
90,9 |
1973 |
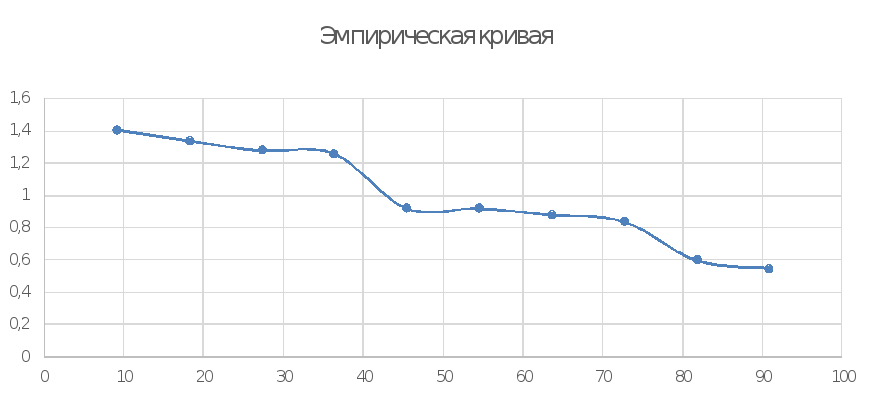
Рисунок – Эмпирическая обеспеченности
