
- •Цепь постоянного тока
- •Применение законов Кирхгофа для расчета электрических цепей постоянного тока
- •Первый закон кирхгофа
- •Второй закон кирхгофа
- •Баланс мощности в цепях постоянного тока
- •Эквивалентные преобразования схем
- •Метод контурных токов
- •Метод двух узлов
- •Метод наложения
- •Входные и взаимные проводимости
- •Двухполюсники
- •Эквивалентные преобразования и двухполюсники
- •Переменный ток
- •Символический метод расчета цепи переменного тока
- •Операции с комплексными величинами
- •Элементы цепи переменного тока
- •Последовательное соединение r,l,c элементов
- •Применение законов Кирхгофа для расчета цепей переменного тока
- •Эдс взаимной индукции.
Символический метод расчета цепи переменного тока
Запись переменных сигналов в виде тригонометрических функций не удобно для решения задач, поэтому любую синусоидальную функцию можно представить в виде комплексного числа. Существует 3 формы записи. Обозначим комплексной число 1) z=x+jy. X – действительная часть y – мнимая часть, j – мнимая единица.
2) z=|z|cosφ+j|z|sinφ. φ – аргумент (начальная фаза сигнала) arctg y/x, если z э 1 или 4 четверти
φ=arctg y/x+π, если z э 2 четверти
φ=arctg y/x-π, если z э 3 четверти
|z| - модуль комплексного числа соответствует действующему значению тригонометрической функции.
|z|=
3) показательная форма записи z=|z|*eiφ
ϕ
Имея показательную форму записываю алгебраическую или тригонометрическую форму.
Задание: написать тригонометрическую функцию в виде комплексного числа в 3х формах.

Замечание: комплексная форма записи не учитывает период и частоту изображенных синусоидальных сигналов
U=1,78*е120j=1,78*cos120+1,78jsin120=-0,89+1,53j
Операции с комплексными величинами
U1=10+5j U2=3-8j
Сложение U=U1+U2=10+5j+3-8j=13-3j
Вычитание U=U1-U2=10+5j-(3-8j)=10+5j-3+8j=7+13j
Умножение U1*U2=(10+5j)(3-8j)=30-80j+15j+40=70-65j
Деление U1/U2=(10+5j)(3+8j)/(3-8j)(3+8j)=30+80j+15j-40/9+24j-24j+64=-10+94j/73=-0,137+1,3j
Элементы цепи переменного тока

Учитывает превращение энергии в тепло
j=Im*sinωt u=Um*sinωt, где Um=Im*R

Резистор не вносит дополнительного сдвига фаз и напряжение, и ток на нем совпадает по фазе
φ=0 – угол сдвига. Для цепей переменного тока изображаются векторные диаграммы. На них откладываются вектора сигналов с учетом нужного угла.
Катушка индуктивности.
![]()
L индуктивность L [Гн] герни
L=
u=Um*sinωt
u=L
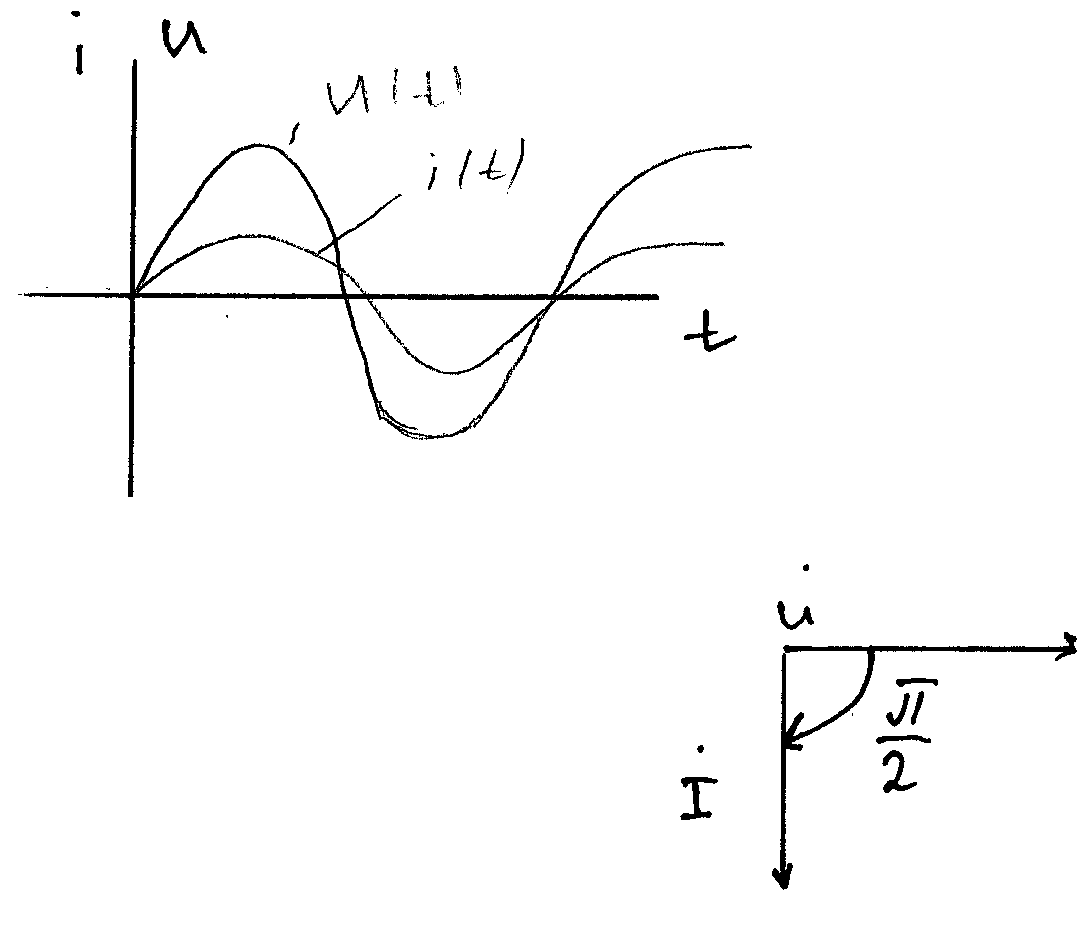
 i=
i=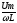 sin(ωt+π/2)
sin(ωt+π/2)

 Im=
Im= гдеωL=Xl
– индуктивное сопротивление
гдеωL=Xl
– индуктивное сопротивление
U=U
если нач фаза=0
I=Ie-j
Катушка создает сдвиг фазы равной 90 . При подаче синусоидального напряжения на катушку ток также синусоидален, но отстает от напряжения на 90 градусов. На векторной диаграмме отстающий вектор изображается по ходу часовой стрелки.

Изобразим 2 схемы
t
Часто требуется определить по осциллографу угол сдвиг фаз между 2мя сигналами. Для этого используем поворот полу периода на целое число клеток, зная, что в одной клетке 5 делений определяем угол с высокой точностью. Из двух синусоид опережающей по фазе является та, которая раньше достигает своих положительных значений при переходе через 0.
 Помимо
индуктивного сопротивления XL
часто используется комплектное
сопротивление в катушке. Обозначается
zL=jXL=jωL.
По закону Ома I=
Помимо
индуктивного сопротивления XL
часто используется комплектное
сопротивление в катушке. Обозначается
zL=jXL=jωL.
По закону Ома I=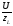
Конденсаторы

Емкость C [Ф] Фарад
U=Um*sinωt
UC= ∫jdt
∫jdt
I=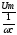 *sin(ωt-π/2)
*sin(ωt-π/2)
Очевидно, что как и катушка конденсатор является фазой сдвигающим элементом. Напряжение и ток синусоидальные, но ток опережает напряжение на π/2
 XC=
XC= – емкостное сопротивление. Используется
комплексное сопротивление конденсаторов
– емкостное сопротивление. Используется
комплексное сопротивление конденсаторов
 ZC=
ZC= =
=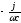 =-jXC
=-jXC

XL=ωL
XC= ω=0
XL=0
XC=∞
ω=0
XL=0
XC=∞
Последовательное соединение r,l,c элементов
 по
закону Ома
по
закону Ома 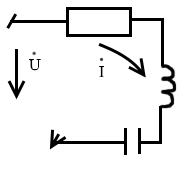
 -
полное сопротивление
-
полное сопротивление




 =
R+zL+zC
, где
zL=jXL=jωL
zC=-jXc=
=
R+zL+zC
, где
zL=jXL=jωL
zC=-jXc= z=R+jωL
z=R+jωL =R+j(ωL
=R+j(ωL )=R+jx
)=R+jx
где
X=ωL =XL-XC
Х
– реактивное сопротивление RLC
– цепи
Если XL>XC,
то
ток будет отставать от напряжения и
цепь носит индуктивный характер <φ
намного меньше π/2.
=XL-XC
Х
– реактивное сопротивление RLC
– цепи
Если XL>XC,
то
ток будет отставать от напряжения и
цепь носит индуктивный характер <φ
намного меньше π/2.
XL<XC цепь носит емкостной характер и ток наоборот опережает напряжение.
При
расчете цепей под действующем значением
используется модуль

 ,
где
,
где
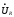 =R*
=R*
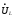 =jωL*
=jωL*
 =jωC*
=jωC*

 >
> >
> Определим
угол сдвига фаз φ между входным напряжением
Определим
угол сдвига фаз φ между входным напряжением и
током
и
током .
Выберем горизонт направления расположения
вектора тока.
.
Выберем горизонт направления расположения
вектора тока.





