Деревья
Последовательность (список) с базовым типом Т - либо пустой список, либо конкатенация элемента типа Т и некоторой последовательности с базовым типом Т
Сложная структура Дерева - это граф.
Дерево с базовым типометр Т - либо пустое дерево, либо некоторые вершины типа Т с конечным числом отдельных поддеревьев с базовым типом ТДерево с базовым типом Т
1) форма с отступами
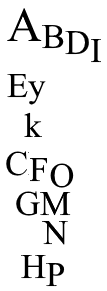
2)в
виде графа
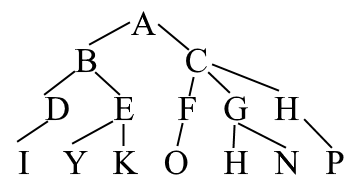
3) с помощью множеств
Упорядоченное дерево. Дерево у которого ребра, сходящие из одной вершины упорядочены. Если в девереве У ниже вершины Х , то у называется потомком, а Х предком. Если у Х уровень I то У лежит на i+1. Корень на уровне 0. Максимальный уровень какой либо из вершин дерева называется его высотой. Если элемент не имеет потомков то его называют терминальной вершиной или листом. Нетерминальная вершина – внутренне. Число непосредственных потомков внутренней вершины называются его степенью. Максимальная степень всех вершин есть степень дерева. Число ветвей которые нужно пройти от корня к вершине х называется длиной пути к х. Корень имеет путь 0, его потомки имеют 1.
Длина всего пути дереве определяется как сумма длин путей для всех его компонентов (длина внутреннего пути).
1*2+2*5+3*7=33 длина примера
Определение пути внешнего пути. Чтобы посчитать дерево дополняем специальными вершинами в тех местах, где в исходной дереве отсутствую подвершины. Все должны быть одной степени(максимальной).
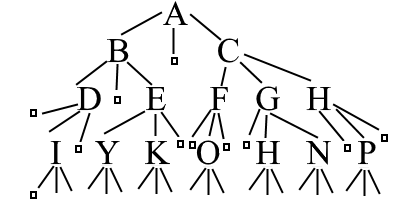
1*3+2*6+3*15+21*4=144
Если в исходном дереве n ребер и добавили m специальных вершин, тогда в расширенном дереве n+m ребер.
Особую роль играют упорядоченные деревья 2й степени. Они называются двоичными или бинарными.
Двоичное упорядоченное дерево – конечное множество элементов, которое либо пусто, либо состоит из корня с 2мя отдельными двоичными деревьями, которые называются левым и правым поддеревом этого корня. Далее говорим только о таких деревьях. Пример двоичного дерева – арифметическое выражение с бинарными операциями.
(a+b/c)*(d-e*f) представим в виде дерева
Представление деревьев. Переменные с динамической структурой (цепные списки). Вершины в дерева – это переменные с фиксированной структурой т.е. тип вершины будет объявлен, а степь дерева будет определять число ссылочных полей, указывающих на вершины поддеревьев. Ссылки на пустые поддеревья равны 0.
конструкция отображающая структуру памяти
Type ptr=^node node=record op:char; //ключевое поле left,right:ptr; *** end:
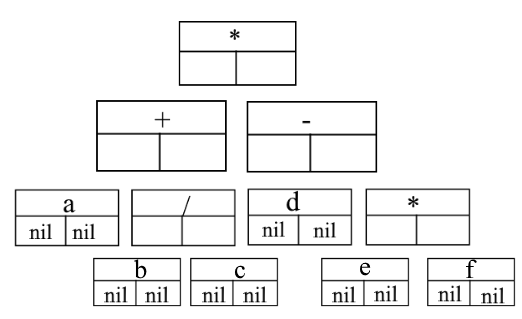
Пример построение дерева. Построим дерево типа ***, построим дерево n-ой вершиной. Этого можно добиться помещая на всех уровнях кроме последнего максимально возможное число вершин. Это получится, если будет размещать приходящие вершины поровну в слева и справа от каждой вершины.
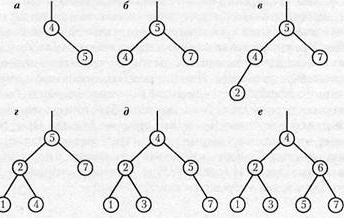
Идеально сбалансированное дерево получаем. Идеально сбалансированное – в котором число вершин в правом и левом поддеревьи отличается не более чем на 1.
1 шаг) взять одну вершину в качестве корня 2) построить тем же способом левое поддерево с nl=n div 2 количеством вершин. 3) построить тем же способом правое поддерево с nr=n-nl-1 количеством вершин.
Рекурсивная функция Блок схема
Function Tree(n:integer):prt; (n – количество вершин, ptr ссылка на построенную ф-ю)
end
N=0
Newnode:=nil
Tree:=newnode
+
Nl=n
div 2
nr=n-nl-1
-
Ввод
х
Getmem(newnode,sizeof(node));
newnode^.key:=x;
newnode^.left:=tree(nl);
newnode^right:=tree(nr);
Можно рисовать с помощью конвы, а можно с Treeview
Основные операции с двоичными деревьями. Самая распрастраненная задача это выполнение некоторой операции p над каждый элементов дерева. Это называется обход дерева.
При реализации этой задачи отдельные вершины проходят в некотором определенном порядке. Существует 3 принципа упорядочивания вытекащие из структуры деревьев. Эти принципы удобно выразить в рекурсивных терминах.
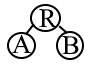
Порядки обхода: 1) preoder:R,A,B (сверху вниз)
2) inorder;A,R,B слева на право
3) postoder:A,B,R снизу вверх
Обойдем пример арифмитического дереве (вверху) каждым способом и получим 3 упорядоченной последовательности.
1)*+a/bc-d*ef
2)a+b/c*d-e*f
3)abc/+def*-*