твн / контрольная / задача2
.docxЗадача №2
Высокочастотный коаксиальный
кабель длиной l
= 17 см расположен на поверхности
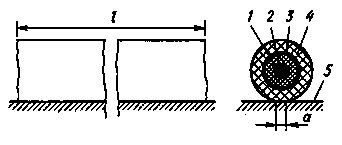
металлического корпуса блока (рис.), где
цифрами обозначено: 1 — внутренний
медный проводник диаметром D1=
0,8 мм; 2
— внутренняя изоляция
из полиэтилена ( 2
= 2,3;
2
= 2,3;
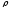 2=1014
Ом∙м); 3 —
медная сетчатая оплетка с внутренним
диаметром D2
= 5,8мм и толщиной
2=1014
Ом∙м); 3 —
медная сетчатая оплетка с внутренним
диаметром D2
= 5,8мм и толщиной
 = 0,4 мм; 4 —
наружный изолирующий слой толщиной h
=1 мм, изготовленный из поливинилхлоридного
пластиката (
= 0,4 мм; 4 —
наружный изолирующий слой толщиной h
=1 мм, изготовленный из поливинилхлоридного
пластиката ( 4
= 6;
4
= 6;
 4
= = 1011
Ом∙м). Рассчитать емкость и сопротивление
изоляции: а) между внутренним проводником
и оплеткой, если кабель разомкнут на
концах; б) между оплеткой кабеля и
корпусом блока, считая, что поверхность
кабеля соприкасается с корпусом 5
на участке размером
4
= = 1011
Ом∙м). Рассчитать емкость и сопротивление
изоляции: а) между внутренним проводником
и оплеткой, если кабель разомкнут на
концах; б) между оплеткой кабеля и
корпусом блока, считая, что поверхность
кабеля соприкасается с корпусом 5
на участке размером
 =0,9
мм.
=0,9
мм.

Решение
а) В
сечении кабеля (рис.) выделим в
полиэтиленовой изоляции 2
участок бесконечно
малой толщины dx,
имеющий координату
х, отсчитываемую
от центра кабеля. Длину окружности
с радиусами х и
x+dx
можно полагать
одинаковой. Тогда сопротивление участка
изоляции толщиной dx
(с координатой х) току
утечки Iут
равно dRx= 2
dx
/(2
2
dx
/(2 xl).
xl).
Сопротивление изоляции между внутренним проводником 1 и оплеткой 3 получим, проинтегрировав выражение для dRx в пределах от x=D1/2 до x=D2/2:
 Ом.
Ом.
Если кабель находится под
напряжением, то вектор напряженности
электрического поля в полиэтиленовой
изоляции направлен по радиусу сечения
кабеля и емкость участка толщиной dx
равна
 .
Отсюда после интегрирования получаем
выражение для расчета емкости между
внутренним проводником и оплеткой:
.
Отсюда после интегрирования получаем
выражение для расчета емкости между
внутренним проводником и оплеткой:
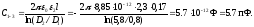
б) Емкость между оплеткой кабеля 3 и корпусом блока 5 может быть определена из формулы для расчета емкости плоского конденсатора, если считать его рабочим диэлектриком наружную изоляцию кабеля 4:

Сопротивление изоляции