
- •1 Выполнение задачи №1 «Сложение синусоидальных сигналов со сдвигом фаз. Теорема косинусов»
- •3. Выполнение задания №3 «Получение периодической последовательности прямоугольных импульсов суммированием гармоник. Построение амплитудного спектра»
- •4 Выполнение задания №4 «Генерация случайного двоичного массива и его визуализация на оси времени»
- •5 Выполнение задания №5 «Моделирование ам, чм и фм модуляторов и наложение шума»
- •6 Выполнение задания №6 «Применение многопозиционных сигналов»
- •7 Выполнение задания №7 «Шифрование текстового файла алгоритмом с симметричным ключом»
1 Выполнение задачи №1 «Сложение синусоидальных сигналов со сдвигом фаз. Теорема косинусов»
Для начала сформулируем необходимые для работы определения.
Сигнал- физический процесс, отображающий сообщение в удобной для передачи по каналу связи форме.
Фаза колебаний — аргумент периодической функции, {\displaystyle \sin(\omega t+\varphi _{0})} {\displaystyle \sin(\omega t+\beta x+\varphi _{0})}описывающей соответственно колебательный или волновой процесс.
Амплитуда колебаний — это наибольшее отклонение колеблющегося тела от положения равновесия.
Построим на оси времени две синусоиды и их суммирующую волну, при заданных значениях периода(T), времени(t) и фазы(ᵩ) (Рисунок1.2).
В рисунке 1.1 представим начальные параметры.

Рисунок 1.1-начальные параметры

Рисунок 1.2 – две синусоиды и их суммирующая волна при фазе = 0
Заметим, что при фазе равной нулю амплитуда колебаний графика суммы двух синусоид равна 2 и что графики S1 и S2 принимают одинаковые значения (рисунок 1.2).
Теперь
построим две синусоиды и их суммирующую
волну, при этом изменив значение фазы
на
 (Рисунок 1.3).
(Рисунок 1.3).
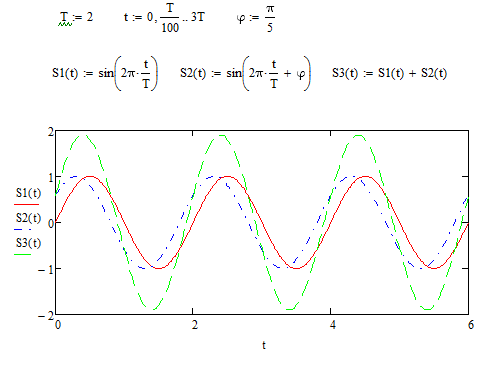
Рисунок
1.3 – две синусоиды и их суммирующая
волна при фазе равной

Заметим,
что при фазе равной
 амплитуда колебаний графика суммы двух
синусоид равна 1.9 и что график S2
отстаёт от графика S1
из-за сдвига фаз(рисунок 1.3).
амплитуда колебаний графика суммы двух
синусоид равна 1.9 и что график S2
отстаёт от графика S1
из-за сдвига фаз(рисунок 1.3).
Сдвиг фаз- разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
Теперь построим две синусоиды и их суммирующую волну, при этом изменив значение фазы на π (Рисунок 1.4).
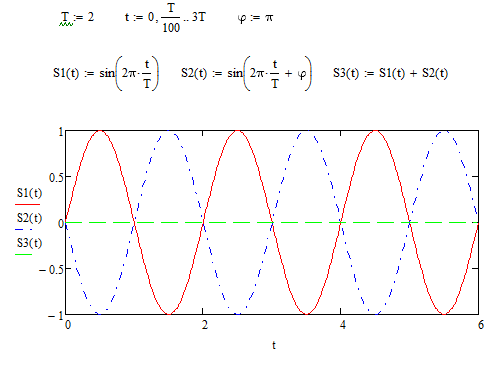
Рисунок 1.3 – две синусоиды и их суммирующая волна при фазе = π
Заметим, что при фазе равной π амплитуда колебаний графика суммы двух синусоид равна 0, так как графики S1 и S2 находятся в противофазе (рисунок 1.3).
Противофаза – момент совпадения максимума одного колебания с моментом минимума другого.
Поэтому при сложении таких графиков получаем ноль.
Теперь
построим две синусоиды и их суммирующую
волну, при этом изменив значение фазы
на
 (Рисунок 1.4) .
(Рисунок 1.4) .

Рис.
1.4 – две синусоиды и их суммирующая
волна при фазе

Заметим,
что при фазе равной
 амплитуда колебаний графика суммы двух
синусоид равна 1.6 и что график S2
отстаёт от графика S1
из-за сдвига фаз(рисунок 1.4).
амплитуда колебаний графика суммы двух
синусоид равна 1.6 и что график S2
отстаёт от графика S1
из-за сдвига фаз(рисунок 1.4).
Теперь
построим две синусоиды и их суммирующую
волну, при этом изменив значение фазы
на 2 (рисунок 1.5).
(рисунок 1.5).

Рисунок 1.5 - две синусоиды и их суммирующая волна при фазе 2π
Заметим, что при фазе равной 2π амплитуда колебаний графика суммы двух синусоид равна 2 и что графики S1 и S2 принимают одинаковые значения (рисунок 1.5).
Вывод: при построении графиков я заметил закономерность, что при фазе [0;π] амплитуда графика суммы двух синусоид уменьшается, а при фазе [π;2π] увеличивается.
Правило параллелограмма- если два неколлинеарных вектора a и b привести к общему началу, то вектор с=а+b совпадает с диагональю параллелограмма, построенного на векторах a и b (рисунок 1.6). Причем начало вектора c совпадает с началом заданных векторов.

Рисунок 1.6 – правило параллелограмма
Для нахождения суммы векторов необходимо:
-
Отложить от точки A вектор АВ равный а и вектор АС равный b;
-
Достроить фигуру до параллелограмма и провести диагональ;
-
Диагональ параллелограмма- это сумма векторов.
Из правила параллелограмма следует теорема косинусов (рисунок 1.7):

Рисунок 1.7- теорема косинусов
Где ᵩ-угол между A и B
А и В- складываемые векторы
Если взять вектора а и b равными 1, то получим выражение(Рисунок 1.10):

Рисунок 1.10- выражение, полученное из теоремы косинусов
В полярных координатах построим график зависимости длины результирующего вектора от угла ᵩ=0 . . 2π (Рисунок 1.11).

Рисунок 1.11 – график зависимости длины результирующего вектора от угла ᵩ=0 . . 2π
Теперь сравним длины результирующего вектора и амплитуды суммы двух гармонических функций S3(t) при одинаковых углах ᵩ (рисунок 1.12).

Рисунок 1.12- сравнение длины результирующего вектора и амплитуды суммы двух гармонических функций
Вывод: Длина результирующего вектора равна амплитуде суммы двух гармонических функций при одинаковых углах ᵩ
