Лаб_6. Выполнение

6. Для каждого кода вычислить кодовое расстояние.

Расстоянием Хэмминга между двумя двоичными векторами x и y, обозначение: d(x, y), называется число позиций, в которых эти векторы отличаются.

Например, d(10111, 00011) = 2.

Кодовым расстоянием или просто расстоянием кода V называется минимальное расстояние между двумя различными кодовыми словами, т. е.

dV = min d(x, y), x ≠ y и x, y Î V.

7. Для каждого кодового вектора вычислить вес.

Весом двоичного вектора, обозначение: w(x), называется число единичных компонент вектора x.

8.Построить стандартное расположение с помощью смежных классов.

9.Для каждого образующего элемента смежного класса вычислить синдром.

10.Построить таблицу кодировок.

11.Выполнить кодирование сообщения длиной в 15-20 символов.

12.Создать модель передачи этого сообщения через канал с помехами.

Генерировать в 80% переданных кодовых слов одну ошибку типа замещение равновероятно в одном из регистров.

13. Выполнить декодирование сообщения.

Все задания требуется выполнить программно в математическом пакете Maple.

2.1 ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

В данном разделе дипломной работы представлен код выполнения лабораторной работы и приведены некоторые методические указания, которые помогут студенту при ее самостоятельном выполнении.

restart; - любая программа написанная в Maple должна начинаться с этой команды, которая требуется для того чтобы перезапустить программу.

Для выполнения лабораторной работы следует после команды restart; подключить модули линейной алгебры:

Листинг 2.1 – Подключение модулей линейной алгебры

with(linalg);

with(LinearAlgebra);

with(LinearAlgebra[Modular])

2.1.1 Выписать все информационные слова i = (i1, i2, i3).

По условию лабораторной работы код размерности V(8,3) Bn (Bn - булево пространство, B = {0,1}, представляет собой множество двоичных векторов длины n) и он является линейным. Следовательно, V - конечное множество, и в подпространстве V существует конечный a1, ..., ak базис из k векторов. Число k называется размерностью линейного кода.

Влинейном (n,k) - коде число k есть размер блока информационных символов, который затем, при кодировании, преобразуется в блок из n символов, где n>k. Добавленные n-k символов называют проверочными символами.

Внашем случаи k=3. Т.е следует выписать все возможные комбинации информационных слов длины равной 3.

Листинг 2.2 – Запись всех информационных слов

i := Matrix([[0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 1, 1], [1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]]) mod 2

Результатом выполнения кода выше будет следующая матрица:

2.1.2 Построить порождающую матрицу G.

Так как V является подпространством линейного пространства, то для задания линейного кода достаточно задать его базис. В этом случае линейный код задается как пространство строк порождающей матрицы G.

Матрица G состоящая из всех базисных векторов линейного кода V называется порождающей матрицей кода V. Строки матрицы G линейно независимы, и число k строк равно размерности кода. Таким образом, порождающая матрица (n,k) - кода имеет размерность k×n.

Делаем вывод что порождающая матрица может иметь не один вид. В случаи, как и с информационными словами, записываем порождающую матрицу.

Листинг 2.3 – Запись порождающей матрицы кода

2.1.3 Найти соответствие между информационными и кодовыми словами. (Построить код).

Если i = a1 ...ak - информационное слово, то соответствующее кодовое слово c=iG. Следовательно, требуется умножить вектор информационных слов на порождающую матрицу кода.

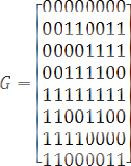
Листинг 2.4 – Построение кода

V:=Matrix(8,8):

V1:=Matrix(8):

for j by 1 from 1 to 8 do V1 := multiply(i[j],G); for k by 1 from 1 to 8 do V[j,k]:=V1[k] mod 2; enddo:

enddo: print(evalm(V));

Получаем следующий код:

2.1.4 Убедиться, что полученный код является линейным (подгруппой).

Полученный код будет являться линейным или подгруппой если при сумме каждого из кодовых слов между собой будет получено слово из того же кода. Т.е код будет линейно независимым – подгруппой.

Листинг 2.5 – Проверка кода на линейность

P1:=Matrix(28,8):

j:=1:

for k by 1 from 1 to 8 do for c by 1 from k+1 to 8 do for z by 1 from 2 to 8 do P1[j,z]:=V[k,z]+V[c,z]mod 2; end do:

j:=j+1: end do: end do:

print(evalm(P1))

После суммирования каждого из слов с каждым получим вектор вида:

Теперь нужно проверить, что каждое из этих слов принадлежит кодовому вектору. Если все слова принадлежат кодовому вектору, код будет линейным или подгруппой.

Следующий код сравнивает каждое слово из вектора суммы со словами из кодового вектора. При наличии совпадения в переменную y присваивается единица. Если в результате выполнения программы переменной y присвоено значение 28, то код является подгруппой.

Листинг 2.6 – Проверка на принадлежность кодовому вектору

y := 0:

for j by 1 from 1 to 28 do for k by 1 from 1 to 8 do if

P1[j][1]=V[k][1]andP1[j][2]=V[k][2]andP1[j][3]=V[k][3] andP1[j][4]=V[k][4] andP1[j][5]=V[k][5] andP1[j][6]=V[k][6] andP1[j][7]=V[k][7] andP1[j][8]=V[k][8] then y:=y+1;

end if; end do: end do:

if y = 28 then print (линейно независимый, т.е код является подгруппой)

else print(линейно зависимый) end if;

Данный код сравнивает каждое слово из вектора суммы со словами из кодового вектора. При наличии совпадения в переменную y присваивается единица.

2.1.5 Найти проверочную матрицу H кода.

Поскольку линейный код V является подпространством, то для него существует ортогональное дополнение (или нулевое подпространство).

Ортогональное дополнение V' (n,k) - кода V состоит из всех векторов длины n, ортогональных к каждому вектору v V. Векторы v1 и v2 называются ортогональными, если их скалярное произведение равно 0.

Ортогональное дополнение также является подпространством и, таким образом, может рассматриваться как линейный код. Множество V' - называется кодом, дуальным или двойственным к V.

Ортогональное дополнение V' (n,k) - кода V имеет размерность (n-k); соответственно любой его базис состоит из (n-k) векторов. Из этого следует, что в нашем случаи проверочная матрица будет состоять из 8 - 3 = 5 векторов.

Порождающая матрица Н ортогонального дополнения называется проверочной матрицей кода V.

Т. к проверочная матрица состоит из базисных векторов ортогонального дополнения, то двоичный вектор с является кодовым словом, если и только если с*НT = 0.

Таким образом, проверка на наличие ошибок при передаче кодового слова сводится к умножению двух матриц

Умножение матриц, размерность которых составляет несколько тысяч, при современной вычислительной технике выполняется очень быстро.

Листинг 2.7 – Нахождение проверочной матрицы

Проверочная матрица кода имеет вид:

H=

2.1.6 Вычислить кодовое расстояние. Вычислить вес кодовых

слов.

Кодовое расстояние, также его называют расстоянием Хэмминга — это число позиций, в которых соответствующие символы двух слов одинаковой длины различны.

Пусть u = (u1, u2, …, un) – двоичная последовательность длиной n. Число единиц в этой последовательности называется весом Хэмминга

вектора u и обозначается как w(u).

Например: u=(1001011), тогда w(u)=4.

Пусть u и v – двоичные слова длиной n.

Число разрядов, в которых эти слова различаются, называется расстоянием Хэмминга между u и v и обозначается как d(u, v).

Например: u=(1001011), v=(0100011), тогда d(u, v)=3.

Легко видеть, что расстояние между двоичными последовательностями u и v равно весу.

Листинг 2.8 – Вычисление кодового расстояния

d := vector(28);

for j by 1 from 1 to 28 do d[j]:=0:

end do; p:=1;

for j by 1 from 1 to 8 do for k by 1 from j+1 to 8 do for l from 1 to 8 do

if V[j,l]≠V[k,l] then d[p]:=d[p]+1 end if

end do; p:=p+1; end do end do

print(evalm(d))

Приведенный выше код выводит все кодовые расстояния:

Листинг 2.9 – Вычисление веса для каждого кодового вектора

w:=ector(8);

for j by 1 from 1 to 8 do w[j]:=0;

end do;

for j by 1 from 1 to 8 do for k by 1 from 1 to 8 do

if V[j,k]=1 then w[j]:=w[j]+1; end if;

end do: end do:

print(evalm(w));

Все кодовые веса:

2.1.7 Построить стандартное расположение с помощью смежных классов.

Можно понизить размерность задачи при исправлении ошибок за счет жесткой математической структуры линейного кода.

Пусть V - линейный код (n, k) - код, v - нулевой вектор и v1, v2, ..., vm - остальные кодовые вектора.

Тогда таблицу декодирования можно составить следующим образом. Кодовые вектора располагаются в виде строки с нулевым вектором слева.

Затем один из оставшихся наборов длины n, например g1, помещается под нулевым вектором.

Обычно это бывает один из наборов, которые наиболее вероятно получится на выходе, если по каналу передавался нулевой вектор.

Далее строка заполняется так, чтобы под каждым кодовым словом vi помещался вектор g1 + vi.

Аналогично в первый столбец второй строки помещается вектор g2, которого еще нет в таблице, и строка заполняется таким же способом.