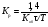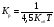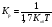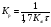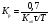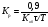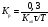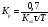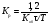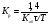Синтез_сушильной_камеры1

Курсовая работа

1. Согласно задания выбрать объект исследования.

Законы регулирования

Различные законы регулирования формируются в соот­ветствующих устройствах. Эти устройства бывают релейные, пропорциональные (П), пропорционально-дифференциаль­ные (ПД), интегральные (И), пропорционально-интеграль­ные (ПИ), пропорционально-интегрально-дифференциальные (ПИД).

П–закон регулирования отработать регулятор может при использовании им величины и знака рассогласования управ­ляемой переменной, т. е. ±Δх.

П – закон автоматического регулятора записывается уравнением вида

u = — К_рΔх, (1.11)

где К_р – коэффициент пропорциональности или усиления.

Знак минус в правой части уравнения (1.11) указывает на то, что во время работы автоматической системы изменение выходного сигнала регулятора ΔX приводит к изменению величины u в обратном направлении.

Графическое изображение П– закона регулирования показано в табл. 1.2.

Таблица 1.2

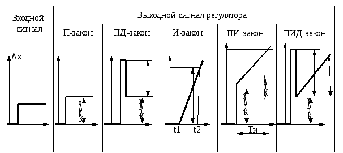
ПИ – закон регулирования отработать регулятор может при одновременном использовании им величины и знака рассогласования ±Δх и интеграла от этого рассогласова­ния ∫Δxdt.

ПИ—закон регулирования записывается уравнением вида

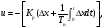(1.14)

ПИ-регуляторы конструктивно выполняют так, что отри­цательная обратная связь в них имеет максимальное воз­действие лишь в начальный момент времени, а затем она постепенно снимается действием инерционной положитель­ной обратной связи.

Коэффициент усиления К_р и время изодрома Т_и являют­ся параметрами настройки ПИ-регулятора.

ПИД – закон регулирования отработать регулятор может при использовании им величины и знака рассогласования ±Δх, а также производной dΔx/dt и интеграла ∫Δxdt от этого рассогласования.

ПИД—закон регулирования записывается уравнением вида

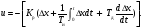(1.15)

Коэффициент усиления К_р, время изодрома T_и и время предварения Т_д являются параметрами настройки ПИД-регулятора.

3.3. Качество регулирования

При выборе типа регулятора следует сформулировать не­обходимые требования к качеству регулирования.

Максимальное динамическое отклонение Х₁ (см. рис. 1.3) является важнейшим показателем характера переходного процесса. Величина его имеет большое значение в случаях, когда по технологическим условиям значительное отклоне­ние от задания недопустимо. Х₁ зависит от динамических свойств объекта регулирования, величины возмущения, при­нятого закона регулирования и настроек регулятора.

Динамический коэффициент регулирования R_д опреде­ляет степень воздействия регулятора, понижающего динами­ческое отклонение, и представляет собой отношение макси­мального отклонения Х₁ к отклонению от задания Х₀ при том же возмущении, но без регулирующего воздействия (см. рис. 1.3).

. (1.16)

Перерегулирование характеризует степень колебательно­сти переходного процесса и определяется отношением вто­рой, противоположно направленной амплитуды колебаний Х₂ к первой Х₁ (рис. 1.3).

Время регулирования охватывает период времени t_р (рис. 1.3) с момента отклонения регулируемой величины до возвращения ее регулятором к заданному значению.

Остаточное отклонение. На рис. 1.3, а регулируемая вели­чина в конце процесса регулирования полностью возвра­щается к заданному значению, а на рис. 3.3,б имеет место остаточное отклонение регулируемой величины от задания, равное ρ.

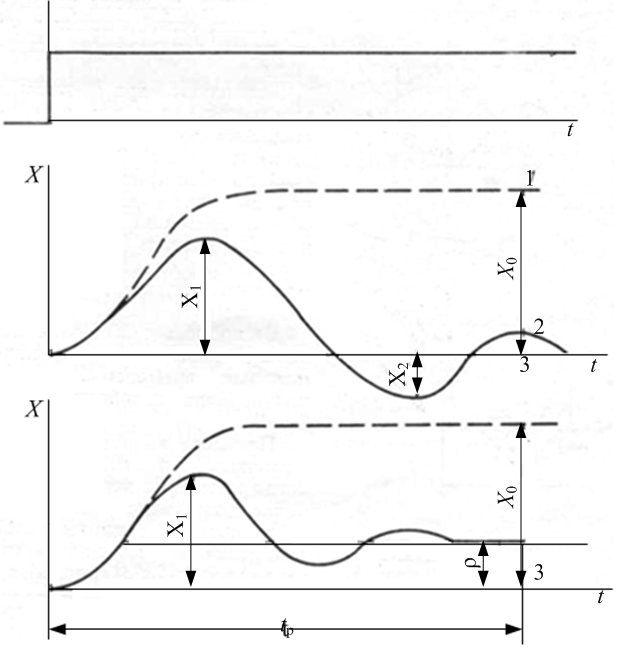
Рис. 1.3. Переходные процессы регулирования: а – без остаточного отклонения;

б – с остаточным отклонением; 1 – без регулятора;

2 – при работе регулятора; 3 – заданное значение

3.4. Оптимальные типовые процессы регулирования

Качество регулирования определяется не только законом регулирования, но и настройками регулятора. При разных настройках одного и того же регулятора можно получить переходные процессы различных типов, отличающиеся друг от друга показателями каче­ства.

Различают три типовых переходных процесса регули­рования:

а) граничный апериодиче­ский процесс (рис. 1.4,а), ха­рактеризуется минимальным общим временем регулирова­ния t_p, полным отсутствием перерегулирования и мини­мальным регулирующим воз­действием;

б) процесс с 20%-ным пе­ререгулированием и мини­мальным временем первого полупериода колебаний (рис. 1.4,б).

Процесс является проме­жуточным и используется, когда некоторое перерегулиро­вание допустимо;

в) процесс с минимальной квадратичной площадью от­клонения min ∫x²dt (рис. 1.4, в).

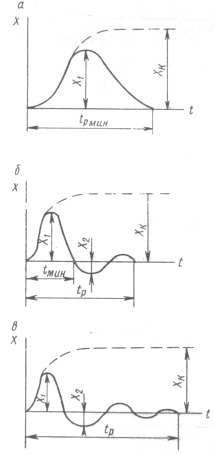
Рис. 3.4. Типовые оптимальные про­цессы регулирования:

а – апериодический; б – процесс с 20%-ным перерегулированием;

в – процесс с минимальной квадратичной площадью отклонения

Процесс отличается наибольшим регулирующим воздействи­ем, перерегулированием (порядка 40 – 45%) и временем ре­гулирования.

Выбор настроек регулятора

Выбор настроек регулятора непрерывного действия на статических объектах производится по данным табл. 1.

В формулах таблицы К_р – коэффициент передачи регу­лятора; T_и – время изодрома; T_п – время предварения.

Таблица 1

Р	Типовой процесс регулирования
	апериодический	20 %-ное перерегулирование	min ∫x2dt
И
П
ПИ	Tи = 0,6 T	Tи = 0,7 T	Tи = T
ПИД	Tи = 2,4τ; Tп = 0,4 τ	Tи = τ; Tп = 0,4 τ	Tи = 1,3τ; Tп = 0,5 τ

Расчет произведем для апериодического процесса регулирования, как более сложного.

Расчет настроек регулятора

П-регулятор

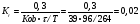
ПИ-регулятор

T_i = 0,6•T = 0,6•264 = 158,4 c

ПИД-регулятор

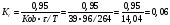
T_i = 2,4•τ = 2,4• 96 =230,4

T_p = 0,4•τ = 0,4•96 = 38,4

Рассмотрим анализ и синтез на примере САР температурой сушильной камеры

Создадим передаточную функцию объекта управления

>> n1=[39]; m1=[264 1]; Wou=tf(n1,m1)

Transfer function:

39

---------

264 s + 1

Создадим САР с П-регулятором.

Передаточная функция П-регулятора:

Создадим САР с П-регулятором.

Передаточная функция П-регулятора:

>> n2=[0.02]; m2=[1]; Kr=tf(n2,m2)

Transfer function:

0.02

>> G=Wou*Kr

Transfer function:

0.78

---------

264 s + 1

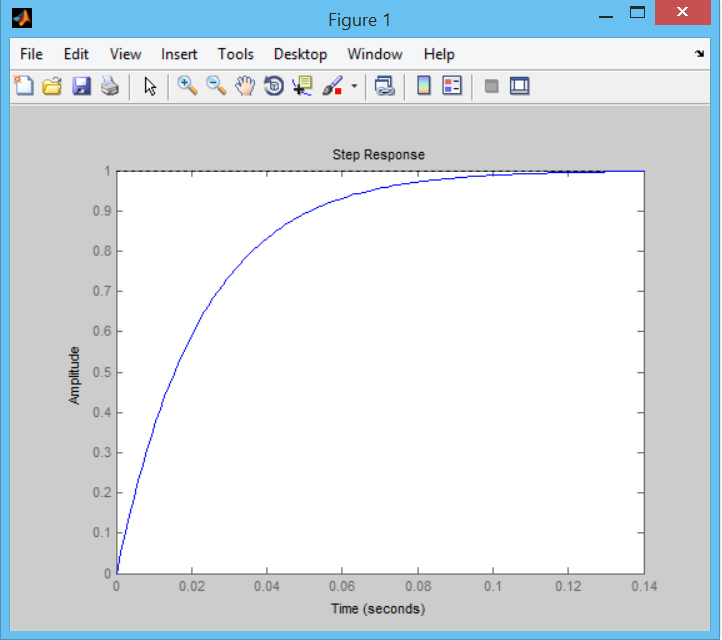
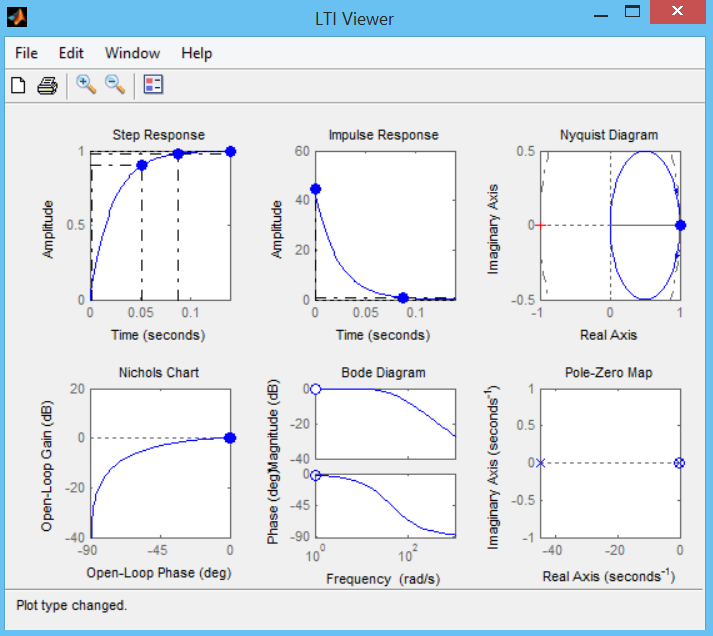
Выполнение функции в формате ltiview (sys) вызывает запуск обозревателя, отображающего заданные аргументом характеристики модели с именем ltiview (G) рис. 1 и открытие в окне обозревателя графика переходной характеристики модели (рис. 1).

Переходная характеристика позволяет определить время регулирования системы с П-регулятором и другие характеристики

Вывод. Время регулирования очень велико – 900 сек. см. рис. 1. Попробуем изменить в сторону уменьшения путем перемещения полюса и введения нуля – рис. 2. Время регулирования 25 сек.

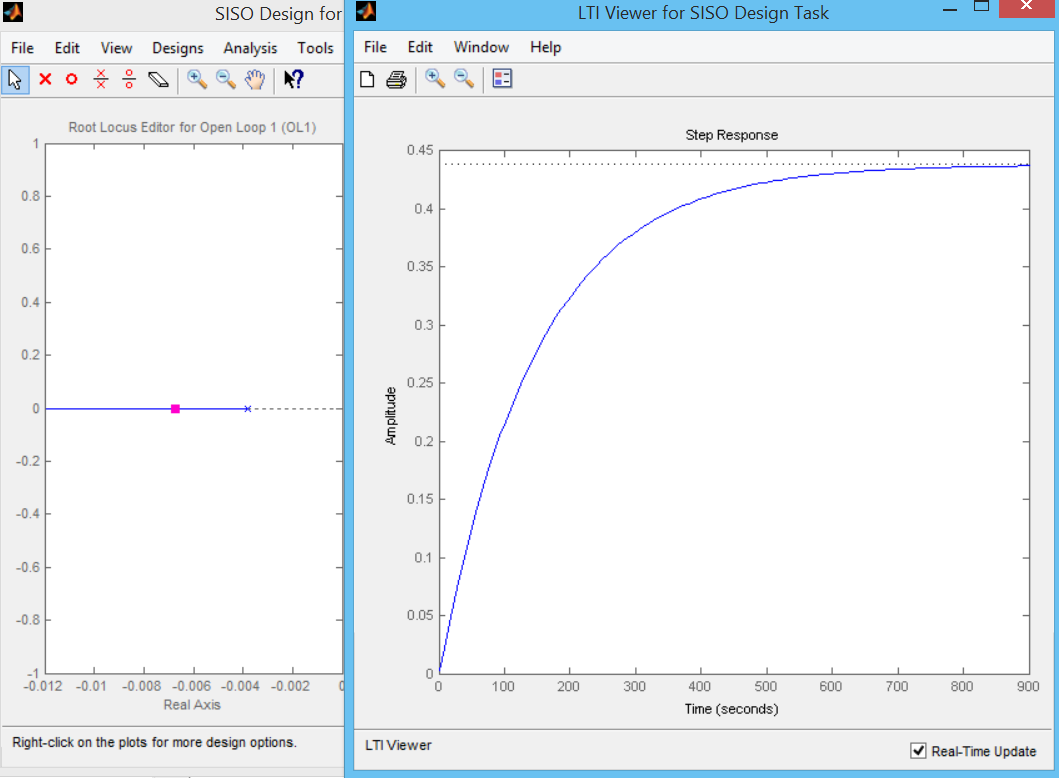
Рис. 1. Время регулирования 900 сек

Рис. 2. Перемещение полюса и введение нуля – время 25 сек

Создадим передаточную функцию ПИ-регулятора

>> n3=[1]; m3=[158,0];Ti = tf(n3,m3)

Transfer function:

1

-----

158 s

>> Gpi = Kr + Ti

Transfer function:

41712 s + 1

-----------

158 s

Создадим передаточную функцию системы с ПИ-регулятором

>> Wpi = Wou*Gpi

Transfer function:

1.627e006 s + 39

-----------------

41712 s^2 + 158 s

Переходная характеристика с ПИ-регулятором представлена на рис. 3.

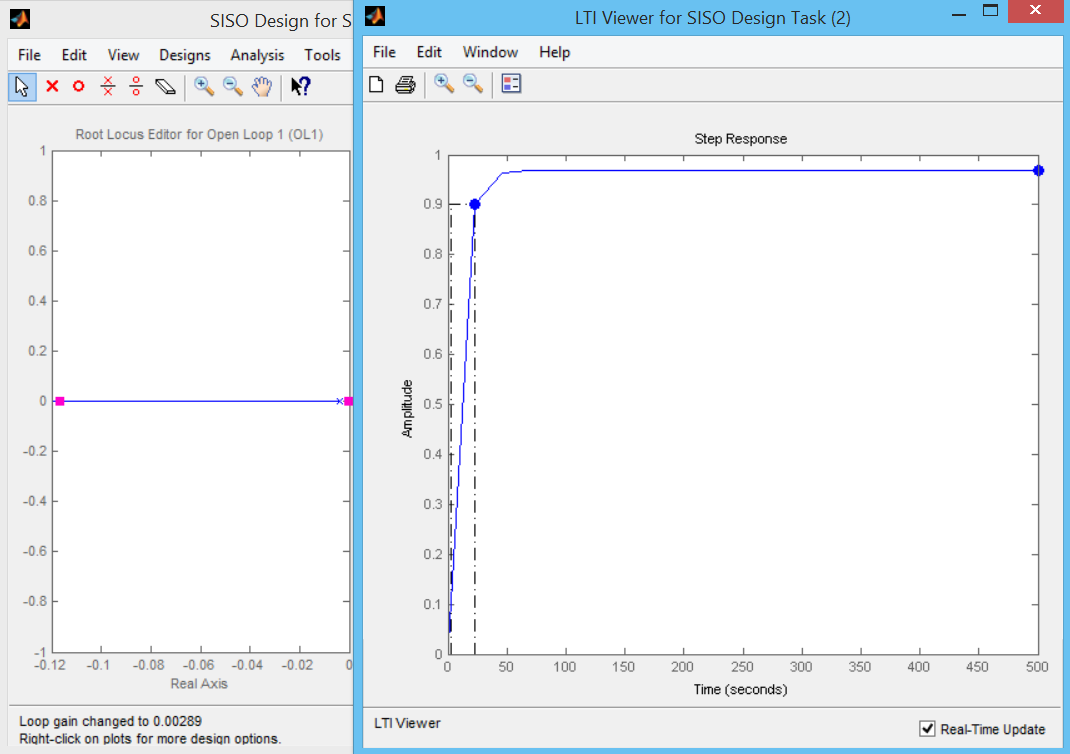
Рис. 3. Переходная характеристика с ПИ-регулятором. Время регулирования 500 с

Время регулирования 500 с, что очень велико. Путем смещения полюса и введения нуля получим время регулирования 15 с. – рис. 4.

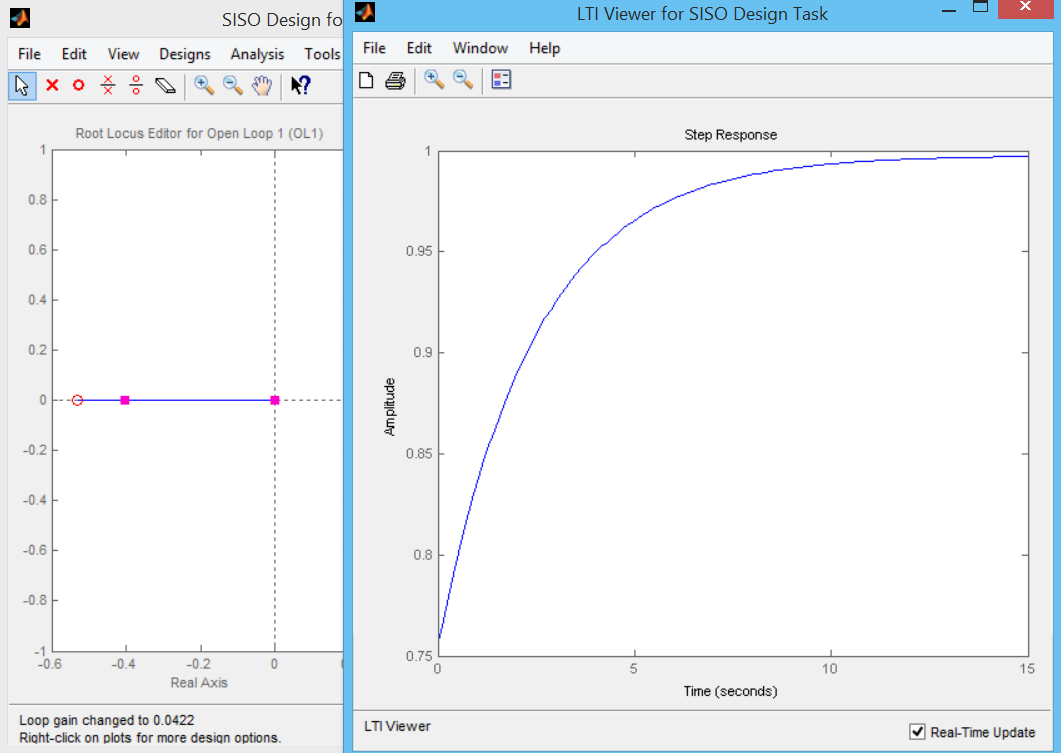
Рис. 4. Переходная характеристика после коррекции. Время регулирования 15 с

Создадим передаточную функцию ПИД-регулятора

>> n3 = [38]; m3=[1]; Td = tf(n3, m3)

Transfer function:

38

Передаточная функция ПИД-регулятора будет иметь вид:

>> Wr = Kr + Ti + Td

Transfer function:

69460 s + 1

-----------

230 s

Передаточная функция разомкнутой САР равна произведению Wr*Wou

>> WRR = Wr*Wou

Transfer function:

2.709e006 s + 39

-----------------

60720 s^2 + 230 s

Найдем переходный процесс для разомкнутой САР – на рис. 5. Переходный процесс имеет не правильную форму и большое время регулирования

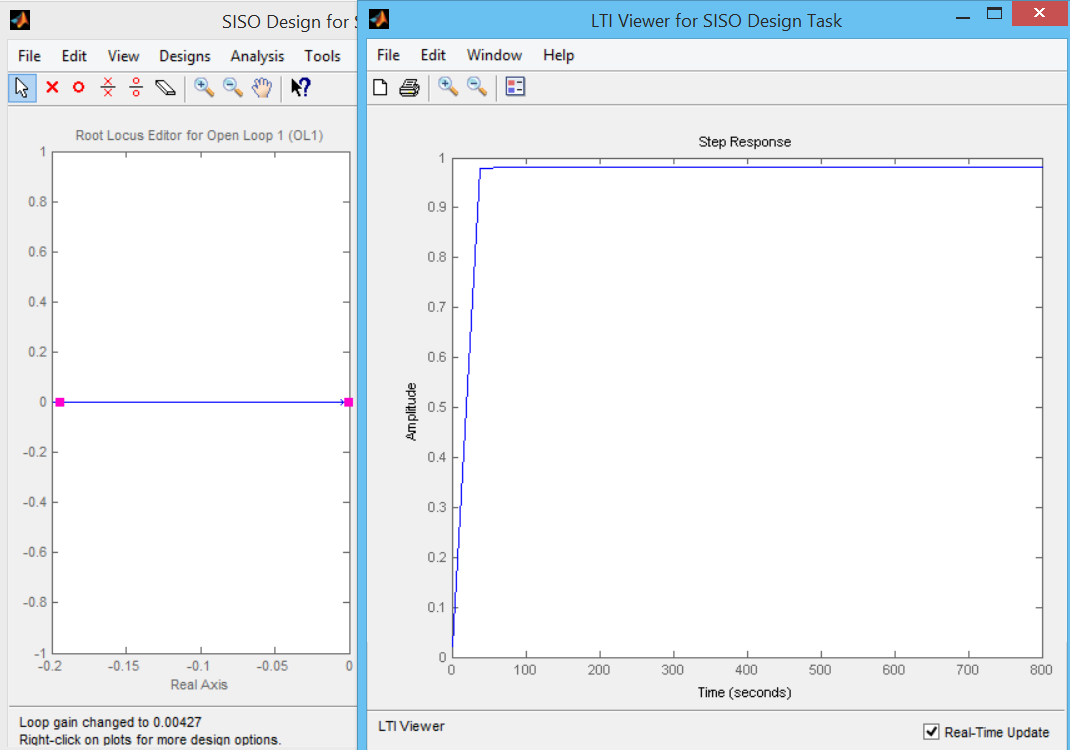
Рис. 5. Переходный процесс разомкнутой системы WRR

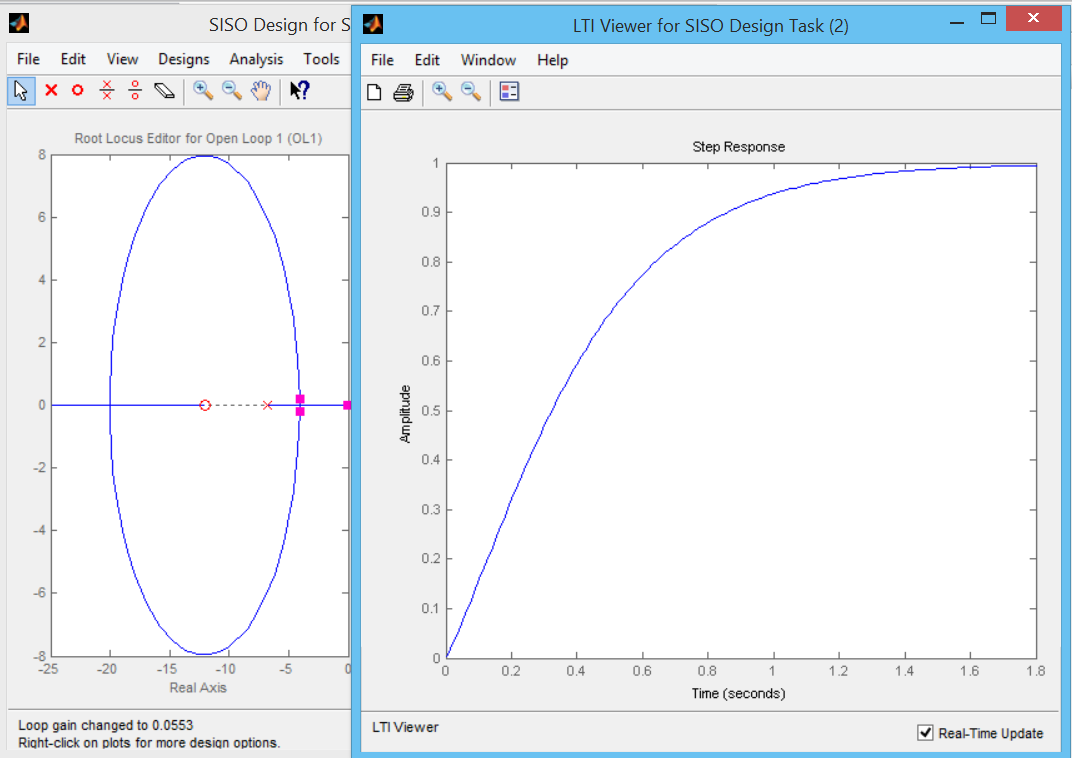
Рис. 6. Переходный процесс разомкнутой САР после коррекции

Замкнем систему отрицательной обратной связью с помощью функции feedback (sys) и определим характеристики замкнутой САР Wzam.

>> Wzam = feedback(WRR,[1])

Transfer function:

2.709e006 s + 39

----------------------------

60720 s^2 + 2.709e006 s + 39