Основные понятия нечеткой логики

К основным понятиям нечеткой логики относятся понятия «нечеткое множество» и «лингвистическая переменная».

Нечеткое множество характеризуется непрерывной функцией принадлежности (ФП), которая может принимать любые промежуточные значения между 0 и 1. ФП отображает все значения x базового множества Х на интервал [0, 1]:

: X [0, 1]

и устанавливает каждому значению x степень его принадлежности к нечеткому множеству А.

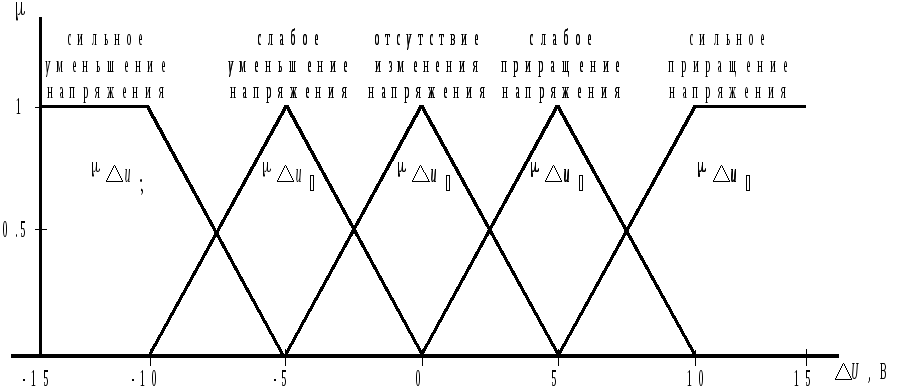
Лингвистической называют переменную, которая задана на лингвистической шкале базовой переменной х и принимает значения в виде слов и фраз естественного языка. Отдельное значение лингвистической переменной, или лингвистическое значение (терм) задается с помощью одной ФП, т. е. каждому терму соответствует нечеткое множество. Лингвистическая переменная УМЕНЬШЕНИЕ НАПРЯЖЕНИЯ ={«сильное уменьшение напряжения», «слабое уменьшение напряжения» и т. д. }. В фиг. скобках – лингв. значения.

Операции с нечеткими множествами

Известные в булевой алгебре логические операции инверсии («НЕ»), конъюнкции («И»), дизъюнкции («ИЛИ»), производимые с логическими переменными 0 и 1, соответствующими ложному и истинному высказываниям, используют ФП , текущие значения которых можно рассматривать как степени истинности, принимающие значения от 0 до 1, включая все промежуточные значения.

Инверсией нечеткого множества А (), заданного на базовом множестве Х, называют нечеткое множество С, ФП которого имеет вид:

(1)

Конъюнкцией (пересечением ) двух нечетких множеств А и В, заданных на общем базовом множестве Х, называют нечеткое множество С, ФП которого имеет вид:

(2)

Дизъюнкцией (объединением ) двух нечетких множеств А и В, заданных на общем базовом множестве Х, называют нечеткое множество С, ФП которого имеет вид:

(3)

Нечеткий логический вывод

Процедура нечеткого вывода основана на операции логического следования (импликации), используемой в традиционной математической логике.

Импликация позволяет формализовать знание эксперта «если А, то В», где А является предпосылкой, а В – заключением. Применительно к задачам нечеткого управления обычно Х – базовое множество значений х управляемой величины, А – некоторое множество значений х, Y – базовое множество значений y управляющего воздействия, В – некоторое множество значений y. Множества А и В находятся здесь в причинном отношении R:

.

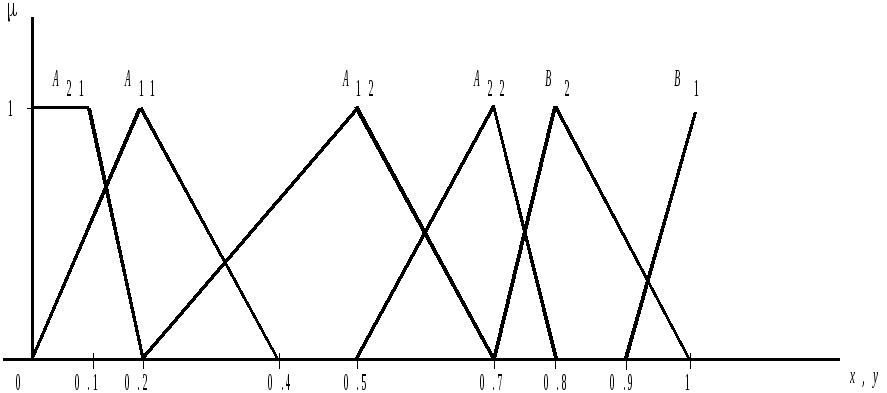
Правило 1: ЕСЛИ И , ТО ,

Правило 2: ЕСЛИ ИЛИ , ТО ,

Входные переменные имеют конкретные значения: и .

1. В соответствии с выражением (2) получаем:

.

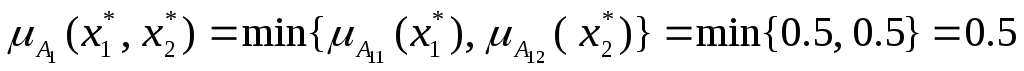В соответствии с выражениями (1), (3) получаем:

.

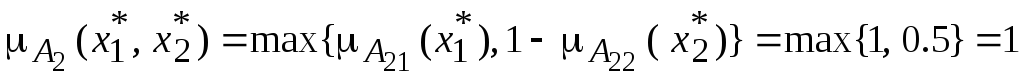2. Усечение ФП по формуле

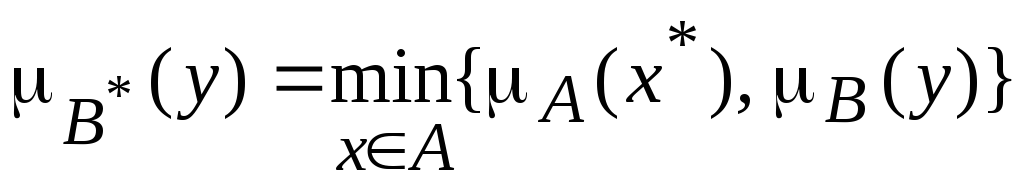
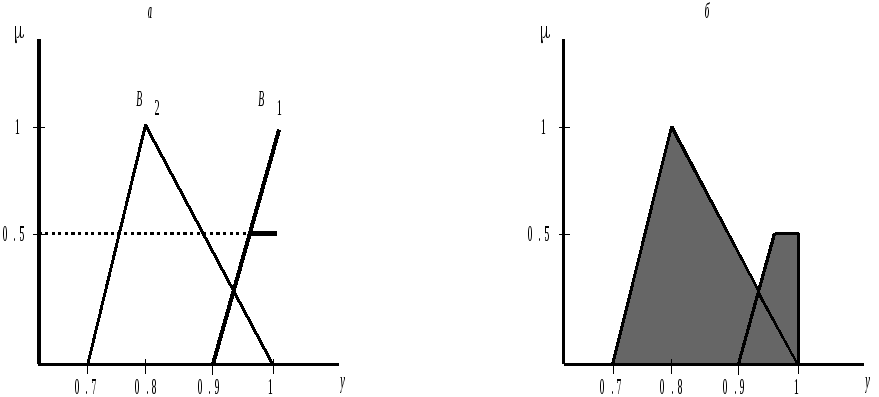
3. Для того чтобы по полученной результирующей ФП найти конкретное значение управляющего воздействия , применяют процедуру дефадзификации. Наиболее распространенным является метод центра тяжести, согласно которому

.

Получаем: .

В заключение раздела необходимо отметить, что существует более ста методов реализации нечетких выводов. Нами были рассмотрены композиции, наиболее часто используемые на практике.