Втюртн В.А. Проектирование систем

В. А. Втюрин,

кандидат технических наук,

Санкт-Петербургская государственная

лесотехническая академия им. С. М. Кирова

Проектирование систем автоматического управления

в пакете Control System Toolbox

В системе MATLAB пакет Control System Toolbox предназна­чен для моделирования, анализа и проектирования систем автома­тического управления (САУ), как непрерывных, так и дискретных [1]. Функ­ции пакета реализуют методы исследования динамических систем, основанные на использовании передаточных функций и моделей для переменных состояния. Частотные и временные характеристики, нули и полюсы системы легко вычисляются и отображаются в виде гра­фиков и диаграмм.

Рассмотрим технологию проектирования на примере САУ температурой плит пресса.

Исходные данные:

Передаточная функция объекта:

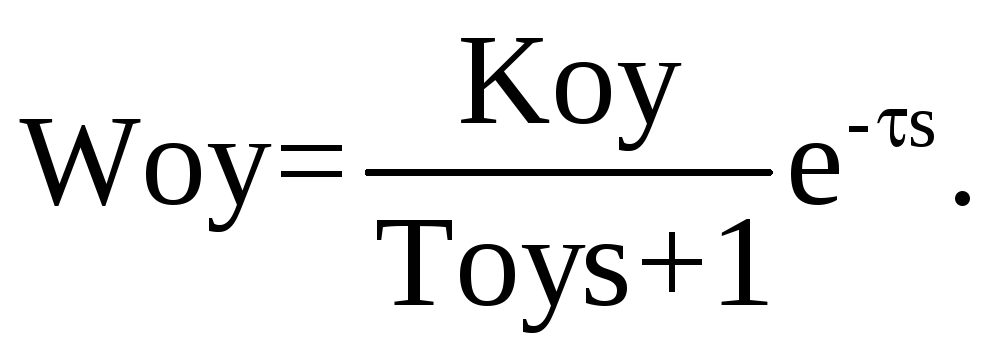
Где: Koy = 0,8 – коэффициент передачи объекта; Toy = 200 с. – постоянная времени объекта; τ = 2 с. – время запаздывания объекта.

Передаточная функция регулятора:

Где Kr = 316 – коэффициент передачи регулятора; Ti = 4,8 – время интегрирования; Td= 0,6 – время дифференцирования.

Передаточная функция замкнутой САУ с учетом запаздывания имеет вид:

1.152 s^4 + 451.5 s^3 - 1361 s^2 + 1364 s + 0.9

GOSZ (s) = ----------------------------------------------------------

961 s^4 + 3343 s^3 + 4263 s^2 + 1380 s + 0.9

Функции MATLAB для создания передаточных функций рассмотрены в [1].

Основными вычислительными объектами рассматриваемого пакета являются:

• родительский объект (класс) LTI (Linear Time-Invariant Systems — линейные, инвариантные во времени системы, в отечественной литературе, обычно называемые линейными стационарными сис­темами);

• дочерние объекты (подклассы класса LTI), соответствующие четырем видам моделей:

I. В так называемой tf-форме (в форме передаточной функции):

(при описании дискретных объектов комплексная переменная) заменяется на z).

2. В zpk-форме (путем задания нулей, полюсов и коэффициента усиления):

(при описании дискретных объектов комплексная переменная р заменяется на z).

3. В ss-форме (в виде системы дифференциальных уравнений для переменных состояния):

(для дискретных объектов — системы разностных уравнений).

4. В frd-форме — в виде набора (вектора) частот w_k и соответствующих значений комплексного коэффициента передачи W(jw_k).

Переход от одной формы к другой реализуется очень легко.

Выполнение функции в формате ltiview(plottype, GOSZ) вызывает запуск обозревателя, отображающего заданные аргументом plottype харак­теристики модели с именем GOSZ. Возможные значения plottype:

• 'pzmap' — карта нулей и полюсов;

• 'step' — отображается реакция на единичный скачок, то есть переходная функция;

• 'impulse' — импульсная характеристика (ИХ);

• 'bode' — диаграмма Боде, то есть ЛАЧХ и ФЧХ;

• 'nyquist' — диаграмма Найквиста, то есть годограф;

• 'nichols' — годограф Николса;

• 'sigma' — отображается зависимость сингулярных чисел комплексного коэффициента передачи системы от частоты.

На рис. 1 показаны примеры реализации некоторых функций: рис. а ­– карта расположения нулей и полюсов позволяет определять устойчивость САУ; б – переходная функция определяет качество регулирования и время регулирования равное 12 с.; в и г – диаграммы Боде и Найквиста определяют запасы устойчивости по модулю и по фазе.

В tf-форме легко и удобно проводить анализ и синтез САУ, но каждый раз при изменении настроек регулятора приходится переписывать передаточную функцию. Такой недостаток отсутствует в zpk-форме.

Переход к zpk-форме можно осуществить с помощью функции rltool, которая открывает графический интерфейс, позволяющий проектировать корректирующее звено в замкнутой одномерной системе управления методом корневого годографа (МКГ).

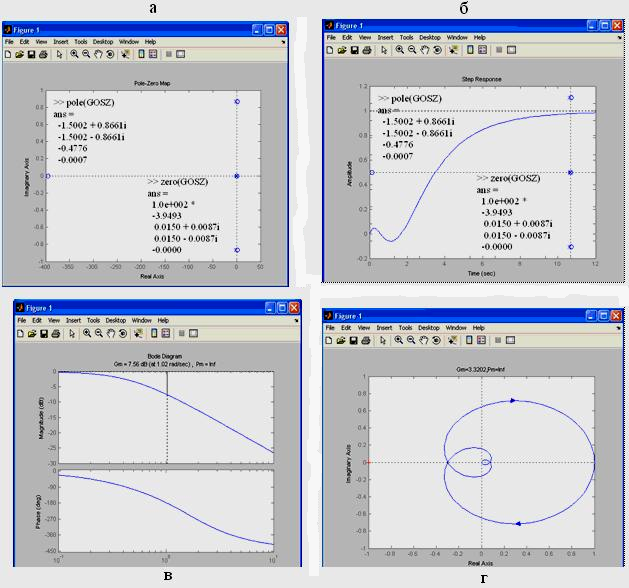
Рис. 1. Примеры выполнения функций: а – 'pzmap' — карта нулей и полюсов;

б ­– 'step' — отображается реакция на единичный скачок, то есть переходная функция;

в – 'bode' — диаграмма Боде, то есть ЛАЧХ и ФЧХ;

г – 'nyquist' — диаграмма Найквиста, то есть годограф.

Функция записывается в следующих формах: rltool, rltool (sys), rltool (sys, comp)

Здесь:

• sys — имя модели одномерного объекта;

comp — имя (идентификатор) корректирующего звена-компенсатора

Перейдем к zpk с помощью функции rltool (GOSZ) и откроется окно на рис. 2. В этом окне, слева вверху, можно добавлять: реальный и комплексный полюс, реальный и комплексный ноль, коэффициент передачи C(s). В графической части окна (на комплексной плоскости нулей и полюсов) отображены полюсы замкнутой системы (квадратиками) нули (кружочками) и линии их перемещения при изменении коэффициента усиления компенсатора (Gain) от указанного (заданного) значения до ∞.

Рис. 2. Окно интерфейса МКГ с загруженной моделью объекта и переходным процессом

В верхнем правом углу окна приведена струк­турная схема замкнутой системы. В ней F, Н, G — звенья, модели ко­торых можно загружать (с помощью переключателя Import From) из рабочей среды MATLAB, из mat-файла или из среды Simulink. Зве­но, обозначенное буквой C, — это компенсирующее ди­намическое звено, структуру и параметры которого нужно определить. В исходной схеме данное звено включено в прямой тракт замкнутой системы – рис 2.а. Нажатием кнопки FS можно перейти к альтер­нативной структуре. На рис. 2.б. для данной структуры получен переходный процесс с перерегулированием, с коэффициентом передачи C(s) = 1. Уменьшим C(s) до 0, 35 рис. 3.а и получим апериодический переходный процесс и время регулирования 8 с. – рис. 3. б.

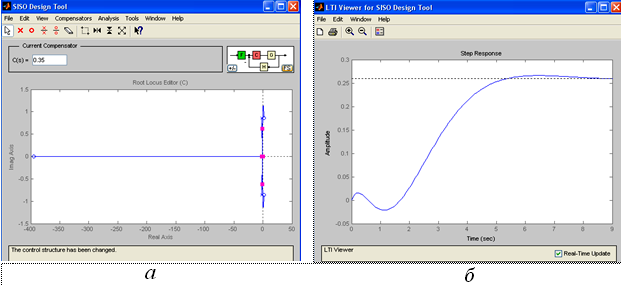
Рис. 3. Переходный процесс в скорректированной САУ

Для получения в одном окне всех одновременно отображаемых графиков можно использовать опцию Plot Configurations меню Edit. На рис. 4. показано окно с различными характеристиками исследуемой САУ.

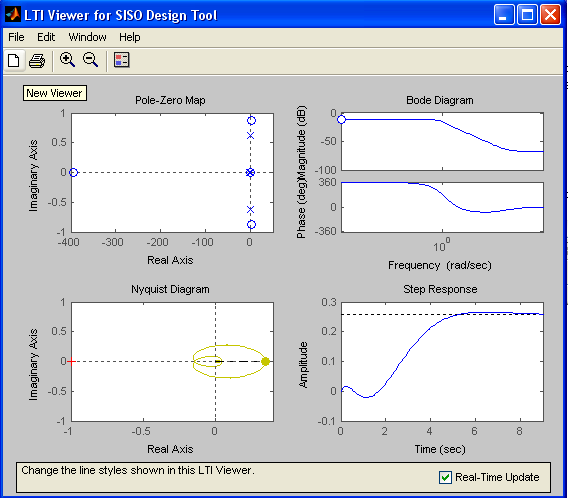
Рис. 4. Окно с различными графиками САУ (GOSZ)

Исследуем САУ (GOSZ) на модели в пространстве состояний, которая связана с записью дифференциальных уравнений в стандартной форме Коши (в виде системы уравнений первого порядка):

Для преобразования передаточной функции в модель в пространстве состояний используем функцию:

>> GOSZ_=ss(GOSZ)

a =

x1 x2 x3 x4

x1 -3.479 -2.218 -0.718 -0.02997

x2 2 0 0 0

x3 0 1 0 0

x4 0 0 0.01563 0

b =

u1

x1 1

x2 0

x3 0

x4 0

c =

x1 x2 x3 x4

y1 0.4657 -0.7108 0.7088 0.02993

d =

u1

y1 0.001199

Это означает, что матрицы модели имеют вид

Определим управляемость САУ GOSZ. Для этого используем функцию Со = ctrb(GOSZ).

>>Co =ctrb(ss(GOSZ))

Co =

1.0000 –3.4787 7.6651 –12.6691

0 2.0000 –6.9573 15.3303

0 0 2.0000 –6.9573

0 0 0 0.0313

>>rank(Co)

Ans = 4

Система является управляемой, если матрица управляемости имеет полный ранг. Возвращаемая величина Co – матрица, имеющая n строк и n×m (столбцов) и описываемая соотношением

>>Ob = obsv (ss(GOSZ))

4657. –0.7108 0.7088 0.0299

–3.0414 –0.3240 –0.3339 –0.0140

9.9320 6.4120 2.1835 0.0911

–21.726 –19.8457–7.1298 –0.2977

>> rank (Ob)

ans = 4

Система является наблюдаемой, если матрица наблюдаемости имеет полный ранг. Возвращаемая величина Ob – матрица наблюдаемости, имеющая n строк и n столбцов и описываемая соотношением

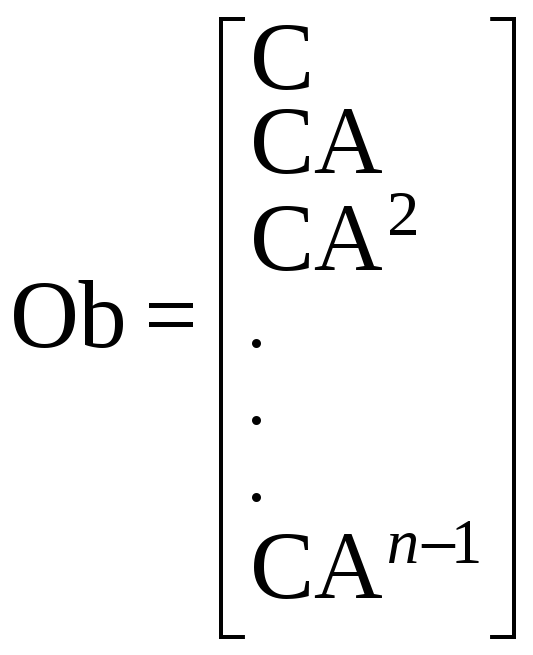
В данном случае ранг матрицы управляемости и наблюдаемости равен 4, и порядок сис­темы — 4, следовательно, система является полностью управляе­мой и полностью наблюдаемой.

Выводы.

1. Модель в формате передаточной функции легко позволяет получить все 7 возможных значений графиков и диаграмм. Однако недостатком является то, что для каждого нового значения переменной, необходимо заново составлять передаточную функцию.

2. Достоинством метода корневого годографа (zpk формы) является то, что в одном графическом окне можно получить одновременно все 7отображаемых графиков. В окне интерфейса можно проводить синтез САУ различными способами: изменением коэффициента передачи системы, нулями и полюсами, изменением структурной схемы САУ.

3. В ss - форме (в виде системы дифференциальных уравнений для переменных состояния) можно определить свойства управляемости и наблюдаемости САУ, не составляя и не решая матриц управляемости и наблюдаемости.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Дьяконов В.П., Круглов В., MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. – СПб.: Питер, 2002. – 448 с.

2. Втюрин В.А., Пашковский И.В., Филимонов Б.А. Анализ систем автоматического регулирования лесосушильных камер. Современные проблемы лесозаготовительных производств, производства материалов и изделий из древесины. Материалы международной научно-практической конференции 27-28 марта 2009 г. 1том. СПб. 2009.

8