
ALL
.pdf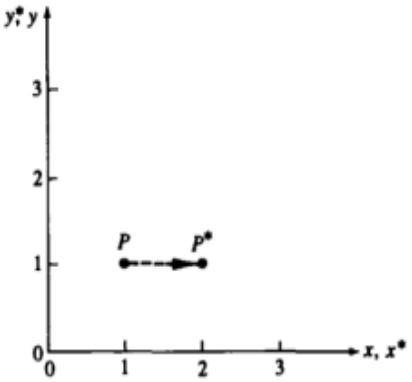
ПРЕОБРАЗОВАНИЕ ТОЧЕК
Специальные случаи. |
d = 1, b = с = 0 |
|
|
|
|||||
X T x |
y |
a |
0 |
ax 0 y |
0x 1y ax |
* |
|
* |
|
0 |
1 |
y x |
y |
|
|||||
|
|
|
|
|
|
|
|
|
|
•где х* = ах — результат масштабирования координаты X.
•Эффект такого преобразования показан на рис. 1,а.
Рис . 1,а
ПРЕОБРАЗОВАНИЕ ТОЧЕК
•Вообще при b = с = 0
X T x |
y |
a |
0 |
ax 0 y |
0x dy ax |
dy x |
* |
y |
* |
|
0 |
d |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
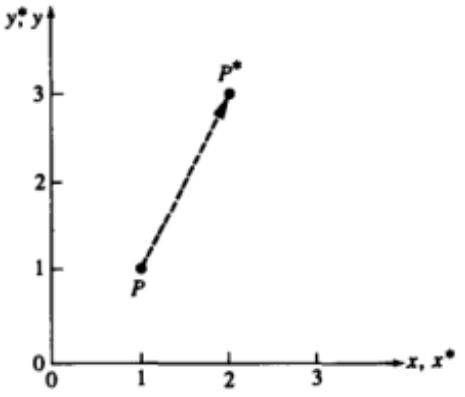
•Данное преобразование вызывает изменение обеих координат х и у вектора Р
•(рис. 1,b).
•Если а d, то координаты масштабируются различным образом.
•При a = d > 1 происходит растяжение вектора Р или масштабирование координат.
•Если 0 < a = d < 1, то сжатие.
Рис . 1,b
ПРЕОБРАЗОВАНИЕ ТОЧЕК
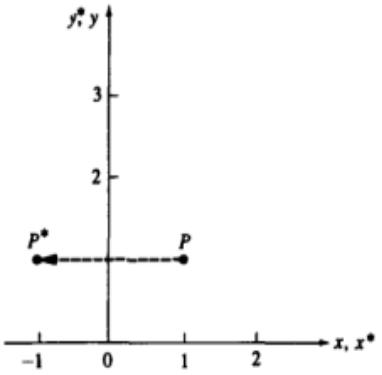
•Если значение а или d отрицательное, то вектор отражается относительно координатных осей или относительно плоскости.
•Пусть b = с = 0, d = 1 и a = -1, тогда
X T x |
y |
1 |
0 |
1x 0 y |
0x 1y x |
y x |
* |
y |
* |
|
0 |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
•в результате получаем симметричное отражение относительно оси у (рис. 1с)
•Если b = с = 0, a = 1, d = –1, то выполняется симметричное отражение относительно оси х.
Рис . 1,с
ПРЕОБРАЗОВАНИЕ ТОЧЕК
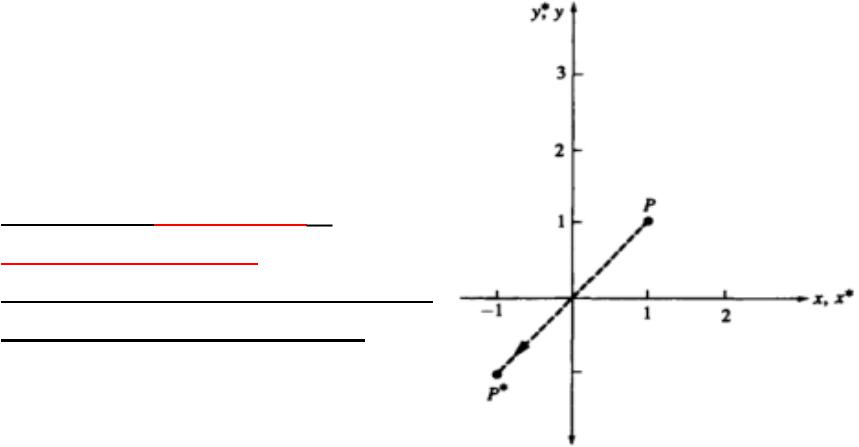
•Если b = с = 0, a = d < 0, то происходит отражение относительно начала координат, это показано на рис. 1,d,
•где a = -1, d = -1.
•Операции отражения и
масштабирование зависят только от диагональных членов матрицы преобразования.
Рис . 1,d
ПРЕОБРАЗОВАНИЕ ТОЧЕК
• Рассмотрим теперь случай с недиагональными членами.
• Пусть a = d = 1, с = 0, тогда |
|
|
|
|
|||||
• |
X T x |
y |
1 |
b |
x |
* |
|
* |
|
|
0 |
1 |
bx y x |
y |
|
||||
|
|
|
|
|
|
|
|
|
|
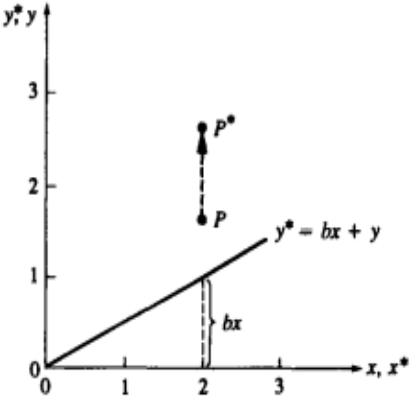
•Заметим, что координата х* точки Р осталась неизменной, тогда как координата у* линейно зависит от исходных координат.
•Данное преобразование называется сдвигом (рис. 1е).
Рис . 1е
ПРЕОБРАЗОВАНИЕ ТОЧЕК
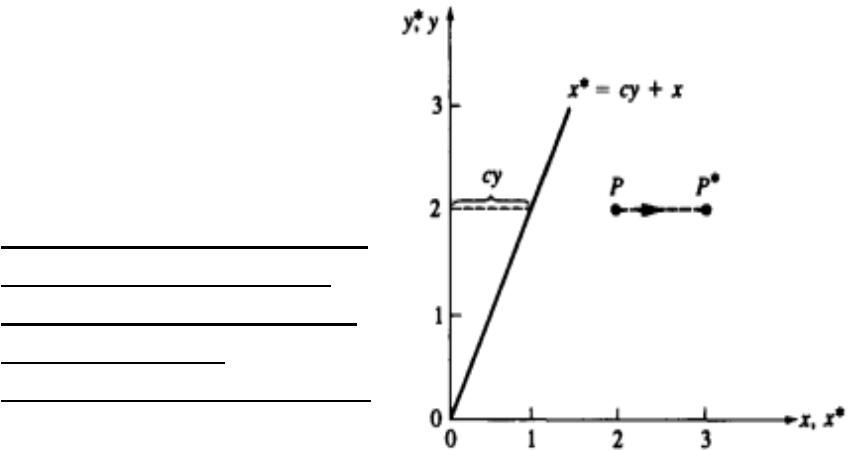
•Аналогично, в случае,
•когда a = d = 1, b = 0,
преобразование приведет к сдвигу пропорционально координате у (рис. 1,f).
•Таким образом, видно, что
недиагональные члены матрицы преобразования создают эффект сдвига координат вектора точки Р.
Рис . 1,f
ПРЕОБРАЗОВАНИЕ ТОЧЕК
•Прежде чем закончить с преобразованием точек, разберем действие общего преобразования, заданного выражением, когда начальный вектор лежит в точке начала координат,
•т. е.
X T x |
y |
a |
b |
ax cy |
bx dy x |
* |
y |
* |
|
c |
d |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
•или, в случае начала координат,
0 |
0 |
a |
b |
0 |
0 x |
* |
y |
* |
|
c |
d |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
•Видно, что начало координат инвариантно относительно преобразования общего вида.
•Это ограничение устраняется при использовании однородных координат.
ПРЕОБРАЗОВАНИЕ ПРЯМЫХ ЛИНИЙ
•Прямую линию можно определить с помощью двух векторов, задающих координаты ее конечных точек, рассмотрим математические операции над
конечными точками линии.
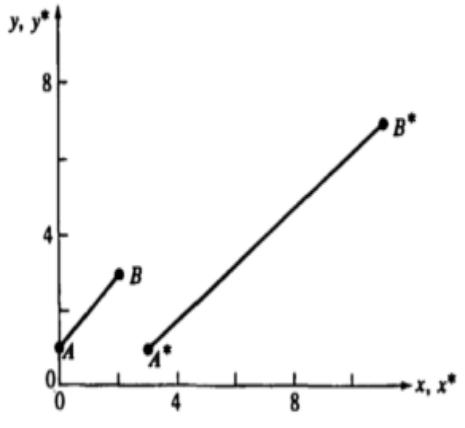
На рис. 2 изображена прямая, проходящая между двумя точками А и В. Положение векторов точек A и В задано следующим образом: [А] = [0 1] и
[В] = [2 3].
Рассмотрим матрицу преобразования
T 1 23 1
Преобразование векторов А и В с помощью матрицы [Т] дает новое положение векторов А* и В*
|
|
|
|
|
|
3 1 A |
|
|
A T 0 1 3 |
1 |
|
||||||
|
|
1 |
2 |
|
* |
|
|
|
|
|
|
|
|
|
11 7 B |
|
|
B T 2 |
3 |
|
|
|
* |
|||
3 |
1 |
|||||||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, результирующие координаты для точки А* – это х* = 3 и у* = 1. Аналогично, для В* : х* = 11, у* = 7.
Рис. 2 Преобразование отрезков.
ПРЕОБРАЗОВАНИЕ ПРЯМЫХ ЛИНИЙ
•В более компактном виде отрезок АВ может быть представлен матрицей 2 х 2:
|
|
|
|
L |
|
0 |
1 |
2 |
3 |
||
|
|
|
|
Умножим эту матрицу на [Т]:
L T |
|
|
|
|
|
|
|
|
|
L |
|
2 |
3 3 |
1 |
11 |
7 |
|||||||
|
0 |
1 |
1 |
2 |
|
|
|
3 |
1 |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
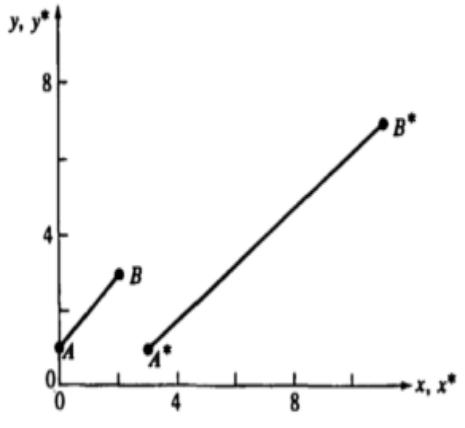
•где компоненты [L*] представляют собой преобразование координаты векторов
•[А*] и [В*].
•Результат преобразования А А* и В В* показан на рис. 2,
•где х и у – это исходные оси координат, а x* и у* — преобразованные оси.
•Из рисунка видно, что преобразование сдвига [Т] увеличивает длину отрезка и изменяет его направление.
Рис. 2 Преобразование отрезков.
ПРЕОБРАЗОВАНИЕ СРЕДНЕЙ ТОЧКИ
• На рис. 2 видно, что 2х2-матрица преобразует прямую линию у = х +1, проходящую между точками А и В в прямую y=3/4x-5/4, которая проходит между точками А* и В*.
• Фактически с помощью 2 х 2-матрицы осуществляется преобразование любой прямой в другую прямую. Все точки преобразованной линии непосредственно соответствуют всем точкам исходной линии. Это достаточно очевидно для конечных точек линии. Рассмотрим теперь преобразование средней точки прямой линии АВ.
• |
Допустим, что |
T |
a |
b |
|
• |
[А]=[х1 у1], [В] = [х2 у2] и |
||||
c |
d |
||||
• |
|
|
|
|
|
Преобразуем одновременно две крайние точки: |
|||||
|
A |
|
x |
y |
|
|
a |
b |
|
|
x a y c |
|
|
|
T |
|
|
|
|
|
|
||||
1 |
1 |
|
|
|
|
1 |
1 |
|||||
B |
c |
d |
||||||||||
|
|
x2 |
y2 |
|
|
|
|
x2a y2c |
||||
x1b y1d |
A* |
|||
x b y |
2 |
d |
|
* |
2 |
|
B |
|
|
•Итак, конечные точки преобразованной линии А* В* имеют следующие координаты
•[А*] = [ах1 + су1 bx1 + dy1] = [х1* у1*],
•[В*] = [ах2 + су2 bх2 + dy2] = [х2* у2*].
