Добавил:

AiSora Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Компьютерная Графика

Файл:

ALL

.pdf

Скачиваний:

278

Добавлен:

12.02.2018

Размер:

15.74 Mб

Скачать

☆

<<< < Предыдущая 36 37 38 39 40 41 42 43 44 45 46 4748 / 6048 49 50 51 52 53 54 55 56 57 58 59 60 > Следующая >>>

08-1

Представления 3D объектов

•Графические сцены могут содержать объекты и материальные поверхности множества различных типов. не существует единого универсального метода, включающего все характеристики данных различных материалов, с помощью которого можно описывать все объекты.

•Многоугольные и квадратичные поверхности позволяют точно описать такие простые евклидовы объекты, сплайновые поверхности и методы конструктивной блочной геометрии полезны при разработке крыльев самолетов, зубчатых передач и других инженерных структур с криволинейными поверхностями, такие процедурные методы, как фрактальные построения и использование систем многих частиц, позволяют моделировать особенности рельефа, облака, заросли травы и другие природные объекты, в методах физического моделирования (physically based modeling) системы взаимодействующих сил используются для описания нежесткого поведения деталей одежды или капли желе, кодирование с помощью октодерева используется для представления внутренних особенностей структуры, полученных, например, по медицинским изображениям компьютерной томографии, кроме того, чтобы визуально представить трехмерные дискретные наборы данных, используются изображения в горизонталях, объемная визуализация и другие методы.

Представления 3D объектов

•Схемы представления твердых объектов делятся на две широкие категории

1.Контурные представления (boundary representations, B-rep) описывают трехмерный объект как набор поверхностей, отделяющих внутреннюю часть объекта от среды. Типичные примеры - описание через грани многоугольника и сплайновые участки.

2.Представления с разбиением пространства (space-partitioning representation) позволяют описывать внутренние свойства через разбиение области пространства, содержащей объект, на набор небольших неперекрывающихся непрерывных объемных тел (обычно кубов). Распространенным описанием трехмерного объекта с разбиением пространства является представление в форме октодерева (octree).

МНОГОГРАННИКИ

•Наиболее распространенным контурным представлением трехмерного графического объекта является указание набора поверхностей-многоугольников, огораживающих внутреннюю часть объекта.

•Часто все описания объектов хранят в форме наборов многоугольных поверхностей. Это упрощает и ускоряет визуализацию - все поверхности описываются линейными уравнениями.

•Многоугольные описания часто называются стандартными графическими объектами. Чтобы

описать объект как набор многоугольных граней

1.Нужно указать координаты вершин всех многоугольных участков поверхности объекта.

2.Затем для каждого многоугольника координаты вершин и информация по краям поверхности записываются в таблицы вместе с информацией о векторе нормали к поверхности.

•Можно генерировать сетки из многоугольных поверхностей наборов треугольников или четырехугольников.

•КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ

•Уравнения объектов с криволинейными границами можно выразить в параметрической или непараметрической форме. В число объектов входят - поверхности второго порядка (квадрики), суперквадрики, полиномиальные и показательные функции, сплайновые поверхности. Входные описания объектов обычно представляются в мозаичной форме, что позволяет аппроксимировать поверхности многоугольными сетками.

•ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

•Поверхности второго порядка (квадрики), описываются уравнениями второго порядка (квадратными) - сферы, эллипсоиды, торы, параболоиды и гиперболоиды. Поверхности второго порядка можно получить с помощью рациональных сплайнов

КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ

•СФЕРА

1.В декартовых координатах сферическая поверхность радиуса r с центром в начале координат определяется как набор точек (x, y, z), удовлетворяющих уравнению.

• x2 + y2 + z2 = r2

2.Сферическую поверхность можно также описать в параметрической форме, используя углы широты и высоты (рис.1).

• x = r cos cos	- /2 /2,
• y = r cos sin	- ,

•z = r sin .

•В параметрическом представлении в формуле принят симметричный диапазон угловых параметров и . В качестве альтернативного варианта параметрические уравнения можно записать, используя стандартные сферические координаты, где угол - задается как дополнение до широты (рис. 2).

•определено в диапазоне 0 , диапазон выбирается равным 0 2 .

Рис. 8.2. Точка с параметрическими координатами (r, θ, ) на поверхности сферы радиуса r

Рис. 8.3. Другое определение сферических координат (r, , )

3.Еще одно представление через параметры u и v, определенные в диапазоне от 0 до 1, можно получить с помощью замены = u и

= 2 v.

ЭЛЛИПСОИД

•Эллипсоидальную поверхность можно описать как расширение сферической, где радиусы в 3х взаимно перпендикулярных направлениях могут иметь различные значения (рис. 1).

1.Декартово представление точек на поверхности эллипсоида с центром в начале координат

Рис 1. Эллипсоид с радиусами rx,

2. Параметрическое представление эллипсоида через угол широты				ry и rz, центрированный в
				начале координат
	и угол долготы (рис.) выглядит так.			начале координат
	и угол долготы (рис.) выглядит так.
•	x = rx cos cos .	- /2 /2,
•	y = ry cos sin ,	- ,	Вид сбоку

•z = rz sin .

•ТОР

•баранкообразный объект. Описывается как поверхность, полученная вращением окружности или эллипса вокруг компланарной осевой линии, не проходящей через коническое сечение.

•Определяющими параметрами тора являются расстояние от центра конического сечения до оси вращения и размеры конического сечения.

•Тор, полученный вращением окружности радиуса r в плоскости yz вокруг оси z, (рис 2). Если центр окружности лежит на оси y,

радиальное расстояние raxial тора равно расстоянию от оси z (ось вращения) по оси y до центра окружности.

•Радиус сечения тора это радиус порождающей окружности.

Вид сверху

Рис 2. Тор с центром в начале координат, имеющий круговое сечение и ось, параллельную оси z

ТОР

•Уравнение поперечного сечения тора (окружности), рис. (проекция сбоку).

• (y – r )2	+ z2 = r2 .
axial

1.Вращая окружность вокруг оси z, получаем тор, точки на поверхности которого в декартовых координатах описываются следующим уравнением.

2.параметрические уравнения для тора с круговым поперечным сечением имеют вид.

• x = (raxial + r cos ) cos , ..

- ,

•y = (raxial + r cos ) sin , .. - ,

•z = r sin .

•Тор можно также получить вращением эллипса вокруг оси z. Уравнение эллипса в плоскости yz, имеющего большую и малую полуось ry и rz,.

•где raxial расстояние от оси вращения z по оси y до центра эллипса.

1.В результате получается тор, уравнение которого в декартовых координатах.

2.параметрическое представление тора с эллиптическим поперечным сечением выглядит так.

•x = (raxial + ry cos ) cos , ..

•y = (raxial + ry cos ) sin , ..

-	,
- ,	,

•z = rz sin .

•поверхность тора можно породить, например, вращением окружности или эллипса по эллиптической траектории относительно оси вращения.

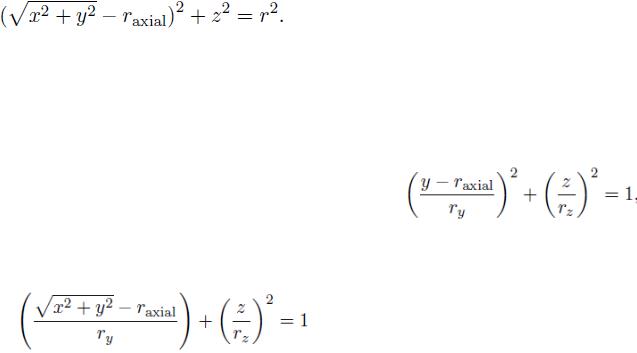
СУПЕРКВАДРИКИ

•Данный класс объектов является обобщением поверхностей второго порядка (квадрик). Для этого в уравнение поверхности второго порядка вводятся дополнительные параметры, что дает большую гибкость в настройке форм объектов.

•В уравнения кривых вводится 1 дополнительный параметр, а в уравнениях поверхностей используются 2 новых параметра.

•СУПЕРЭЛЛИПС

•Представление суперэллипса в декартовых координатах получается из соответствующего уравнения эллипса, в котором степень x и y может меняться.

1. Одним возможным решением является запись декартова уравнения суперэллипса.

•где параметр s может иметь любое действительное значение.

•При s=1 получаем обычный эллипс.

2.	параметрические уравнения суперэллипса, представленного формулой, можно выразить
•	x = rx coss	-

•y = ry sins .

•суперэллиптические формы при различных значениях параметра s.

Рис. 8.6. Суперэллипсы, полученные при различных значениях параметра s из диапазона 0,5 – 3,0 (rx = ry)

СУПЕРЭЛЛИПСОИДЫ

1.Декартово представление суперэллипсоида развивается из уравнения эллипсоида введением в него двух степенных параметров.

•

•При s1 = s2 = 1 получается обычный эллипсоид.

2.параметрическое представление суперэллипсоида, выраженного формулой .

•	x = rx coss1 - coss2θ,	-π /2 π /2
•	y = ry coss1 - sins2θ,	-π θ π

•z = rz sins1

•На рис. иллюстрируются формы суперэллипсоидов, которые можно получить при различных значениях параметров s1 и s2.

•Эти и другие суперквадрики можно объединять, создавая еще более сложные структуры.

КАПЛЕВИДНЫЕ ОБЪЕКТЫ

•Молекулярные структуры, жидкости, плавящиеся объекты и мускулы людей и животных, имеют определенную степень текучести. Все такие объекты называются каплевидными (blobby objects).

•Форму отдельных молекул, можно считать сферической, но она меняется при приближении одной молекулы к другой. ( рис.) Данные характеристики нельзя адекватно описать просто с помощью сферических или эллиптических форм.

•Разработано несколько моделей для представления каплевидных

•объектов как функций распределения в области пространства.

•Формы поверхностей описываются так, что объем объекта остается

•постоянным при любых движениях или взаимодействиях.

Рис. Молекулярные связи.

•1 метод моделирования - использовать комбинацию гауссовых функций плотности (рис. след. слайд). поверхностная функция определяется следующим образом.

•где r2k = x2k + y2k + z2k, параметр T некоторый заданный порог, а параметры ak и bk используются для подгонки степени каплевидностиотдельных компонентов поверхности.

•При параметре bk,< 0 можно получить впадины вместо горбиков.

•На рис. (след.слайд) иллюстрируется структура поверхности сложного объекта, смоделированного четырьмя гауссовыми функциями плотности.

•При пороговых проверках используются численные методы нахождения корней, позволяющие найти координаты точек пересечения.

•Сечения отдельных объектов моделируются окружностями или эллипсами. Если два сечения расположены рядом, они сливаются в одну каплю, структура капли зависит от разнесения объектов.

<<< < Предыдущая 36 37 38 39 40 41 42 43 44 45 46 4748 / 6048 49 50 51 52 53 54 55 56 57 58 59 60 > Следующая >>>

Соседние файлы в предмете Компьютерная Графика

#
12.02.201823.16 Mб881793_1318583371_5516.pdf
#
12.02.201815.74 Mб278ALL.pdf
#
12.02.2018736.4 Кб120fullKG.pdf