ALL

ЭТАЛОННАЯ СИСТЕМА НАБЛЮДЕНИЯ uvn

•Иногда используются левосторонние координаты наблюдения, и наблюдение ведется по

положительному направлению оси zview. В левосторонних системах увеличение значений zview считается удалением от точки наблюдения вдоль линии обзора.

•Современным стандартом компьютерной графики являются правосторонние системы, а левосторонние системы часто используются для представления экранных координат и преобразований нормировки.

•Нормаль к плоскости наблюдения N определяет направление оси zview, а вектор верха V - оси yview, нужно определить только направление оси xview.

•Используя входные значения N и V, можно вычислить третий вектор U, перпендикулярный N и V.

•Вектор U определяет положительное направление оси xview.

•Правильное направление U выбирается по направлению векторного произведения V и N, чтобы в итоге получалась правосторонняя система наблюдения.

•Векторное произведение векторов N и U также дает значение вектора V, перпендикулярного N и U и идущего по положительному направлению оси yview.

•С помощью описанных процедур получаем следующий набор единичных правосторонней системы наблюдения:

Рис. Правосторонняя система наблюдения, определенная единичными векторами u, v и n

•Система координат, сформированная данными единичными векторами, называется эталонной системой наблюдения uvn (рис.).

ПРЕОБРАЗОВАНИЕ ИЗ ВНЕШНИХ КООРДИНАТ В КООРДИНАТЫ НАБЛЮДЕНИЯ

•В 3D конвейере наблюдения первым действием после построения сцены является перенос описаний объектов в систему наблюдения. Это преобразование описаний объектов эквивалентно последовательности преобразований, совмещающих систему наблюдения со внешней системой координат.

•1. Транслировать (сдвиг) начало системы наблюдения в начало внешней системы координат.

•2. С помощью поворотов совместить оси xview, yview и zview с осями xw, yw и zw внешней системы координат соответственно. Начало системы наблюдения находится в точке с внешними координатами P = (x0; y0; z0). Матрица трансляции начала системы наблюдения

•в начало внешней системы координат :

•R матрица поворота, совмещающую оси

•наблюдения с осями внешней системы координат:

•где элементы матрицы R это компоненты осевых векторов uvn.

•Матрица преобразования координат получается умножением T и R:

•Параметры трансляции вычисляются как скалярное произведение

•единичных векторов u, v и n с P0, представляющим вектор, идущий из начала внешней системы координат в начало координат системы наблюдения.

•Параметры трансляции это отрицательные проекции вектора P0 на все координатные оси системы наблюдения. Данные элементы матрицы вычисляются следующим образом:

•Матрица переводит описания объектов во внешней системе

•координат в систему наблюдения.

ПРЕОБРАЗОВАНИЯ ПРОЕКТИРОВАНИЯ

•На следующем этапе трехмерного конвейера наблюдения (после преобразования в координаты наблюдения) описания объектов проектируются на плоскость наблюдения.

•При параллельной проекции точки переводятся на плоскость наблюдения вдоль параллельных линий. На рис. иллюстрируется параллельная проекция отрезка прямой с

конечными точками P1 и P2. Параллельная проекция сохраняет относительные пропорции объектов, параллельные линии сцены остаются такими же на параллельной проекции. Существует два общих метода получения параллельной проекции объекта: проектировать вдоль линий, перпендикулярных плоскости наблюдения, или точки спроектировать под косым углом к плоскости наблюдения.

•Рис. Параллельная проекция отрезка на плоскость наблюдения

•При перспективной проекции положения объектов преобразуются в координаты проекции вдоль линий, сходящихся к точке за плоскостью наблюдения. (Рис.). В отличие от параллельной, при перспективной проекции не сохраняются относительные пропорции объектов. Однако перспективные проекции сцены более реалистичны, поскольку удаленные объекты после проектирования выглядят меньшими.

•Рис. Перспективная проекция отрезка на плоскость наблюдения

АКСОНОМЕТРИЧЕСКИЕ И ИЗОМЕТРИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ

•Наиболее распространенная аксонометрическая проекция - изометрическая, которая получается таким согласованием плоскости проекции (или объекта), при котором эта плоскость пересечет все координатные оси, по которым определен объект (называются главными осями), на одинаковом расстоянии от начала координат. (рис.)

•Чтобы получить эту проекцию, вектор нормали к плоскости наблюдения выравнивается вдоль диагонали куба. Всего существует восемь точек (по одной в каждом октанте), в которых можно получить изометрическую проекцию. На изометрической проекции все три главные оси сокращены одинаково, поэтому сохраняются относительные пропорции.

•Для общей аксонометрической проекции подобное утверждение неверно, здесь масштабные коэффициенты могут быть разными

втрех главных направлениях.

•Рис. Ортогональное проектирование объекта с изображением вертикальной и горизонтальной проекций

•Рис. Изометрическая проекция куба

АКСОНОМЕТРИЧЕСКИЕ И ИЗОМЕТРИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ

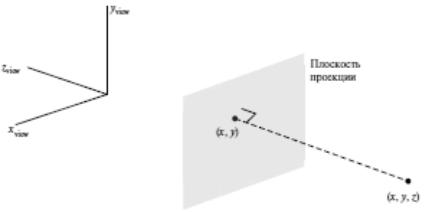
•Рис. Ортогональная проекция точки пространства на плоскость наблюдения

•КООРДИНАТЫ ОРТОГОНАЛЬНОЙ ПРОЕКЦИИ

•Когда направление проектирования параллельно оси zview, уравнения преобразования ортогональной проекции тривиальны.

•Для любой точки (x; y; z) в координатах наблюдения, как показано на рис., координаты проекции выражаются так:

•xp = x;

•yp = y

•Напомним, что при любом преобразовании проектирования значение координаты z записывается для использования в процедурах определения видимости. Кроме того, каждая трехмерная точка сцены преобразуется в точку в нормированном пространстве.

ОТСЕКАЮЩЕЕ ОКНО И ОБЪЕМ НАБЛЮДЕНИЯ ОРТОГОНАЛЬНОЙ ПРОЕКЦИИ

•Размер ортогонального объема наблюдения по оси zview можно ограничить одной или двумя дополнительными граничными плоскостями, параллельными плоскости наблюдения.

•Плоскости называются ближней/дальней плоскостями отсечения или передней/задней плоскостями отсечения. Ближняя и дальняя плоскости позволяют исключать объекты, находящиеся перед или позади части сцены, которую требуется отобразить. Если наблюдение

ведется по отрицательному направлению оси zview, выбирается zfar < znear, дальняя плоскость лежит дальше по отрицательному направлению оси zview.

•Рис.. Конечный ортогональный объем наблюдения

•отсекается плоскостью наблюдения перед

•ближней плоскостью

•

•Получаем конечный ортогональный объем наблюдения - прямоугольный параллелепипед, (рис.) где также представлено одно возможное расположение плоскости наблюдения.

•Проекция сцены будет содержать только те объекты, которые принадлежат объему наблюдения, а вне этого объема удаляются алгоритмами отсечения.

•Ближняя и дальняя отсекающие плоскости могут располагаться произвольным образом по отношению друг к другу, что позволяет получать различные эффекты наблюдения, в том числе изображать точки, расположенные на противоположных сторонах от точки наблюдения.

•Плоскость наблюдения часто выбирается совпадающей с ближней плоскостью отсечения.