
5
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
отчет
по лабораторной работе №5
дисциплина - «Моделирование систем»
Тема: «Моделирование эпидемии»
|
Студент гр. 5371 |
|
Уруков С.Д. |
|
Преподаватель |
|
Туральчук К.А. |
В данной лабораторной работе произведено моделирование динамической системы. Построена модель, показывающая изменение популяции.
Мы рассмотрели 4 модели:
Модель 1. Неограниченный рост.
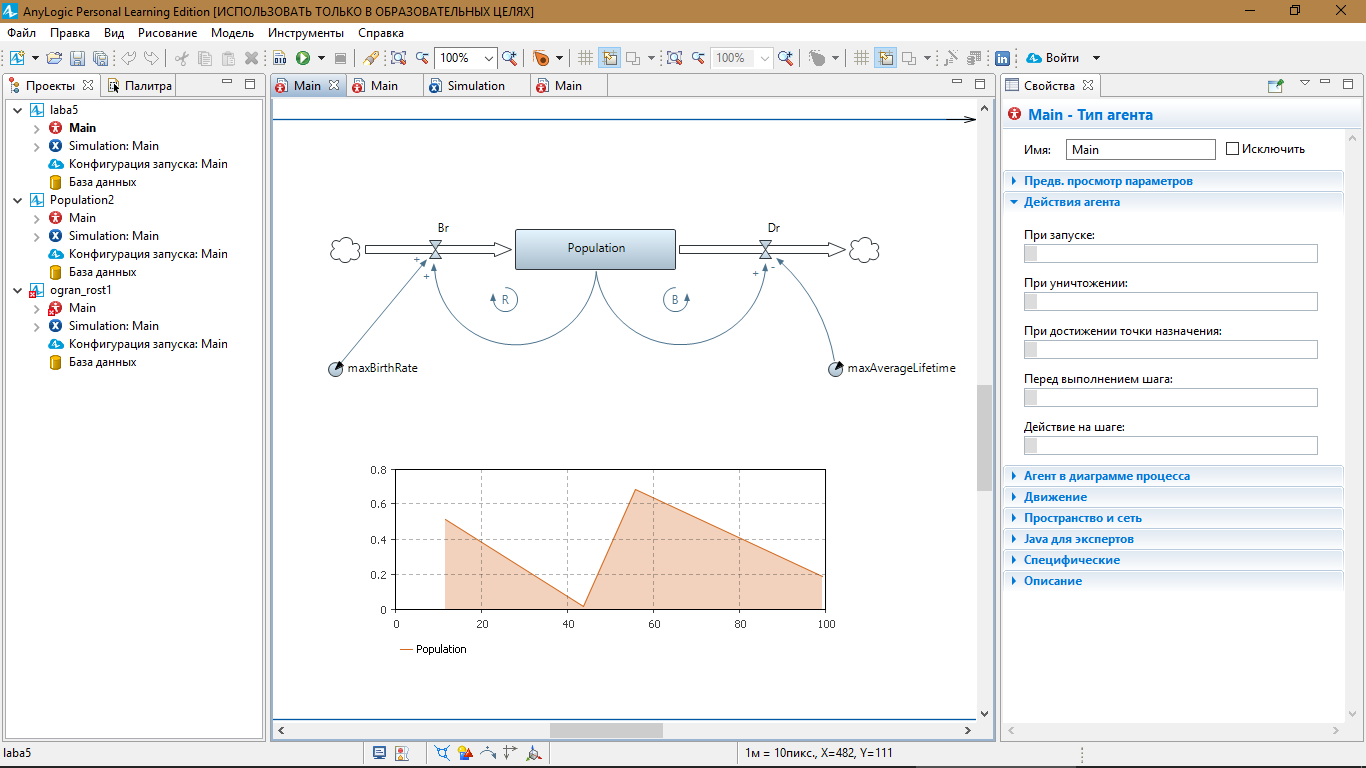
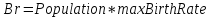
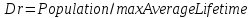
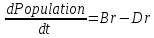
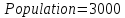
maxBirthRate = 0.07; maxAverageLifetime = 84; спустя 60 сек. Population = 98000.
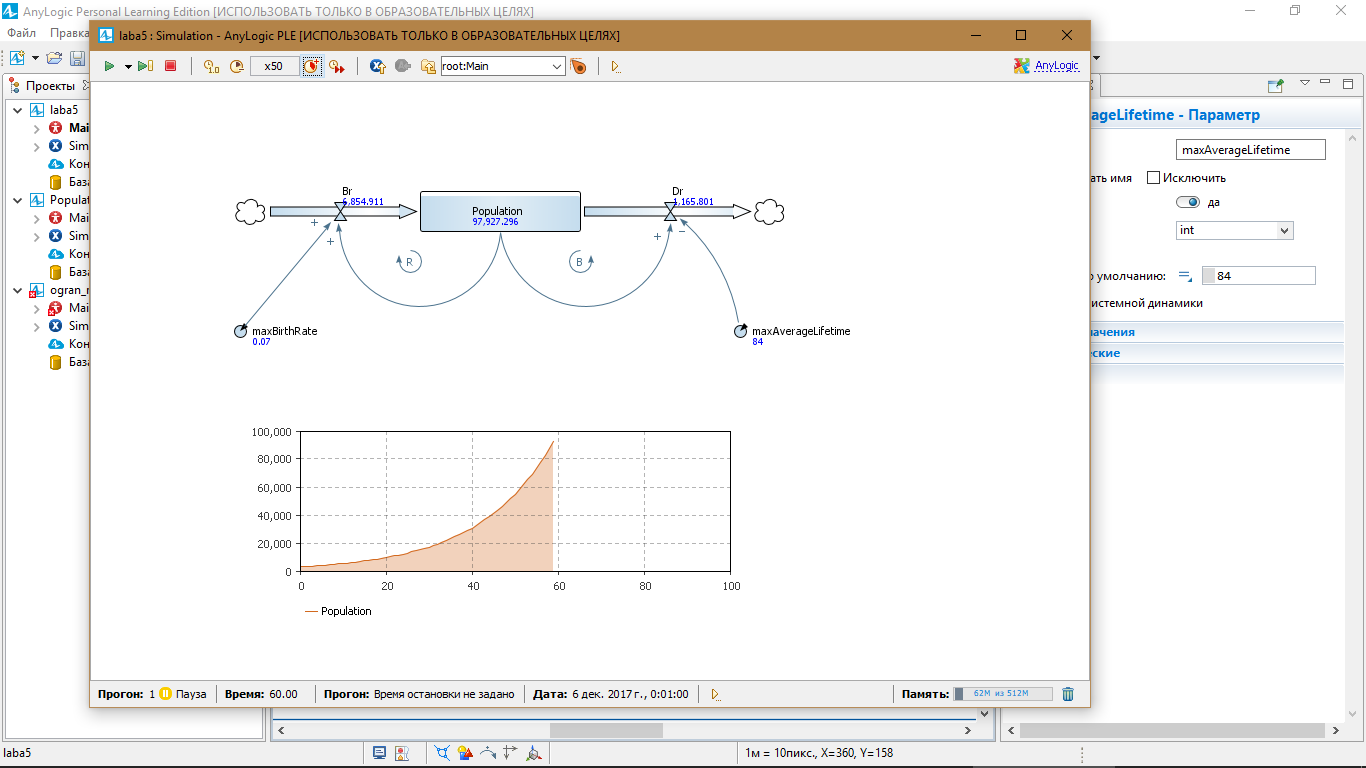
maxBirthRate = 0.04; maxAverageLifetime = 70; спустя 60 сек. Population = 14000.
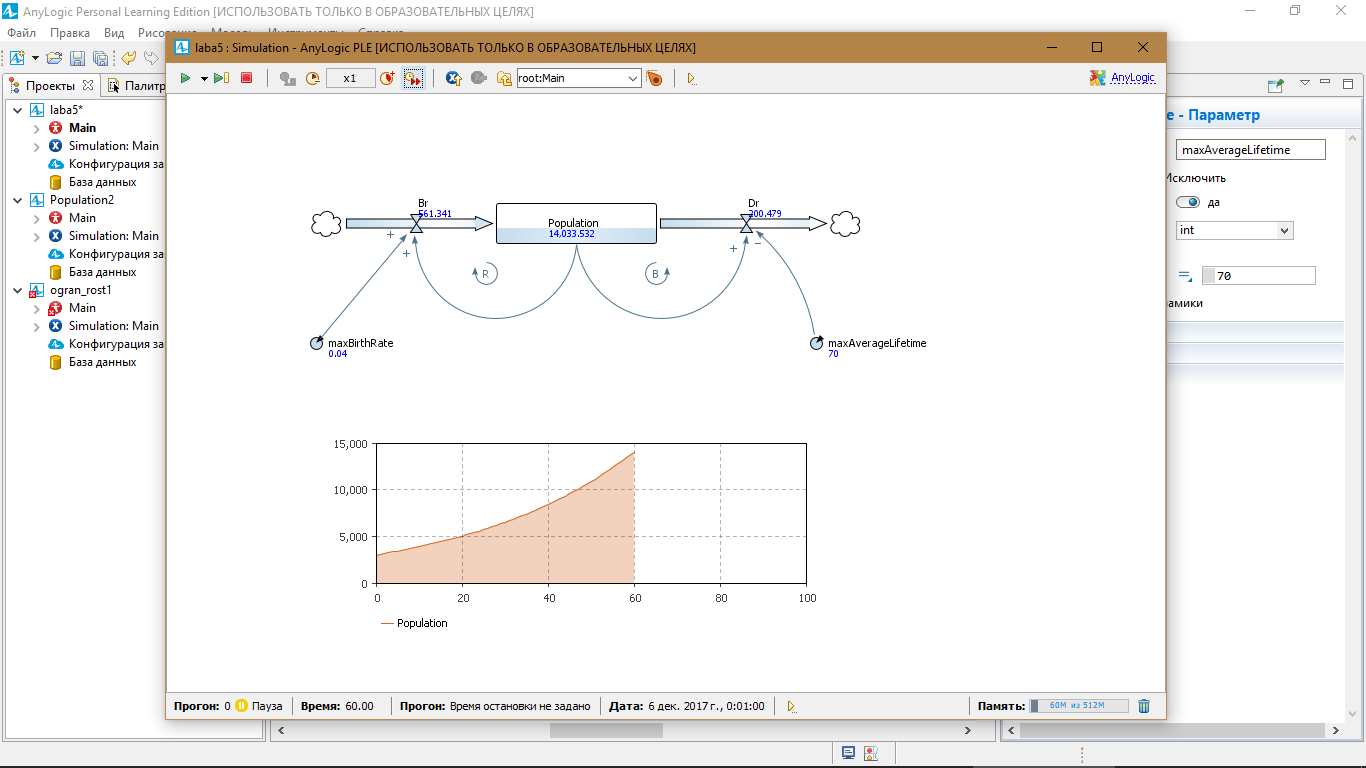
maxBirthRate = 0.08; maxAverageLifetime = 70; спустя 60 сек. Population = 14000.
maxBirthRate = 0.01; maxAverageLifetime = 70; спустя 60 сек. Population = 2319.
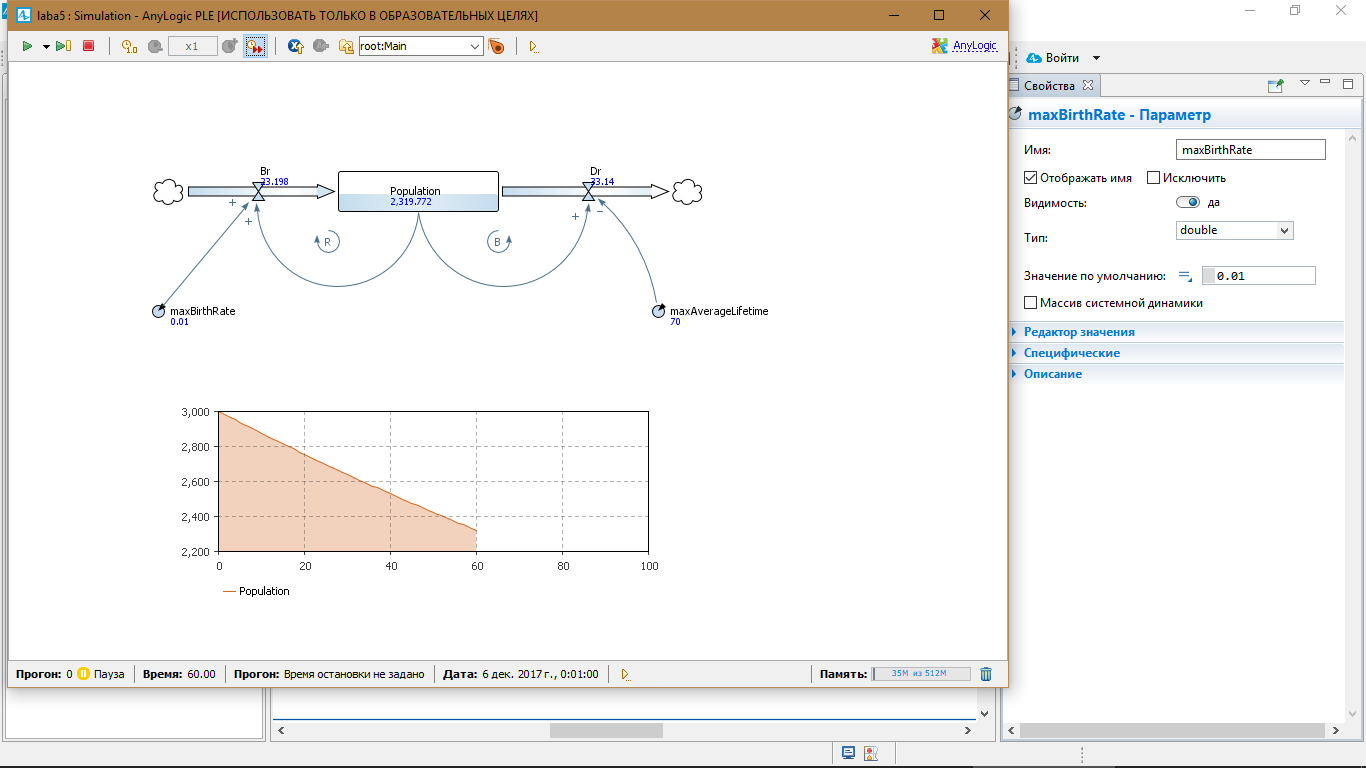
Модель 2. Ограниченный рост.
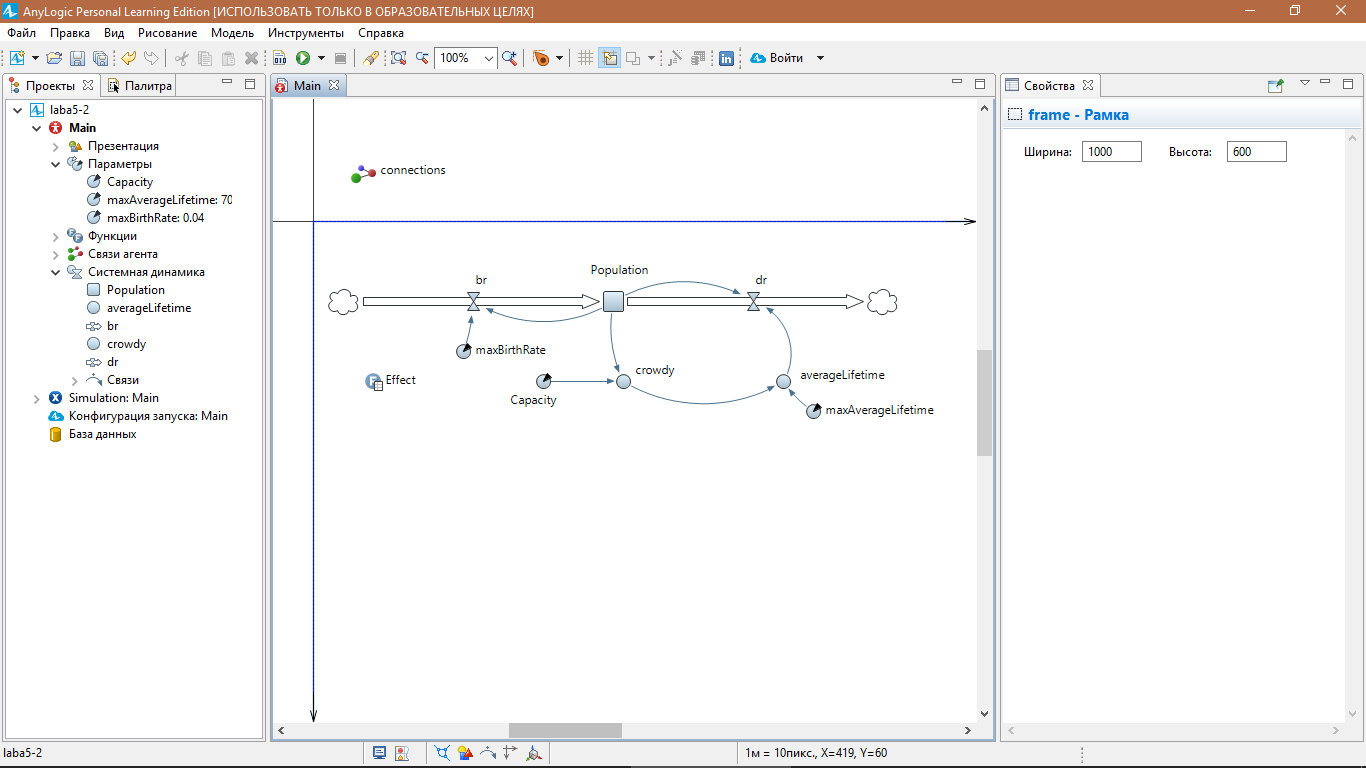
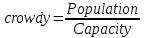
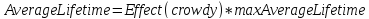
Для Capacity = 5000
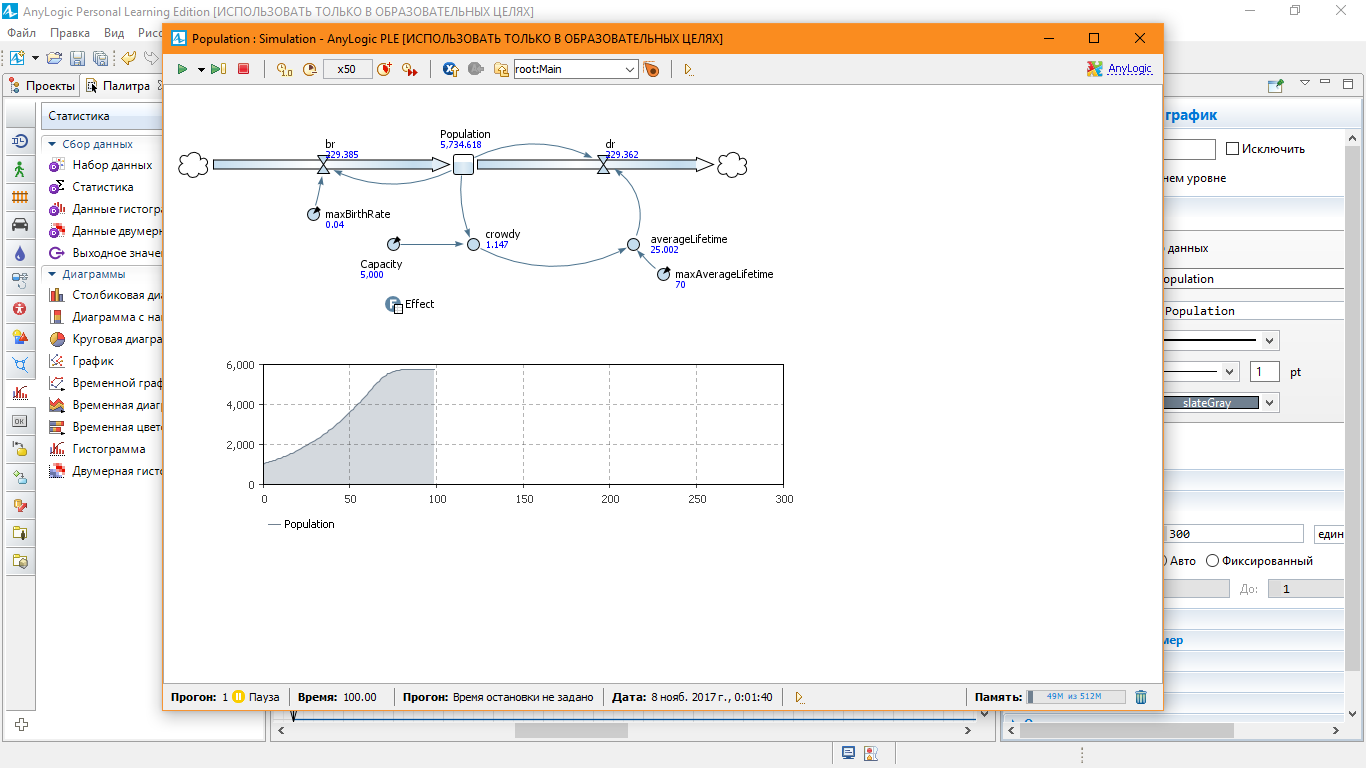
Для Capacity = 2000
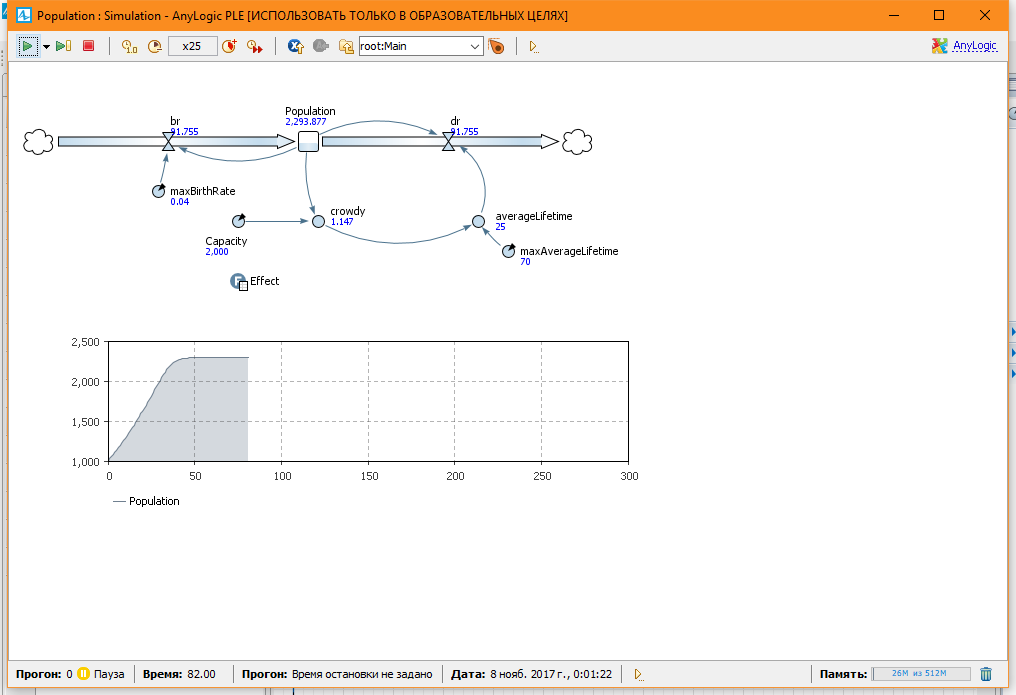
Для Capacity = 25000
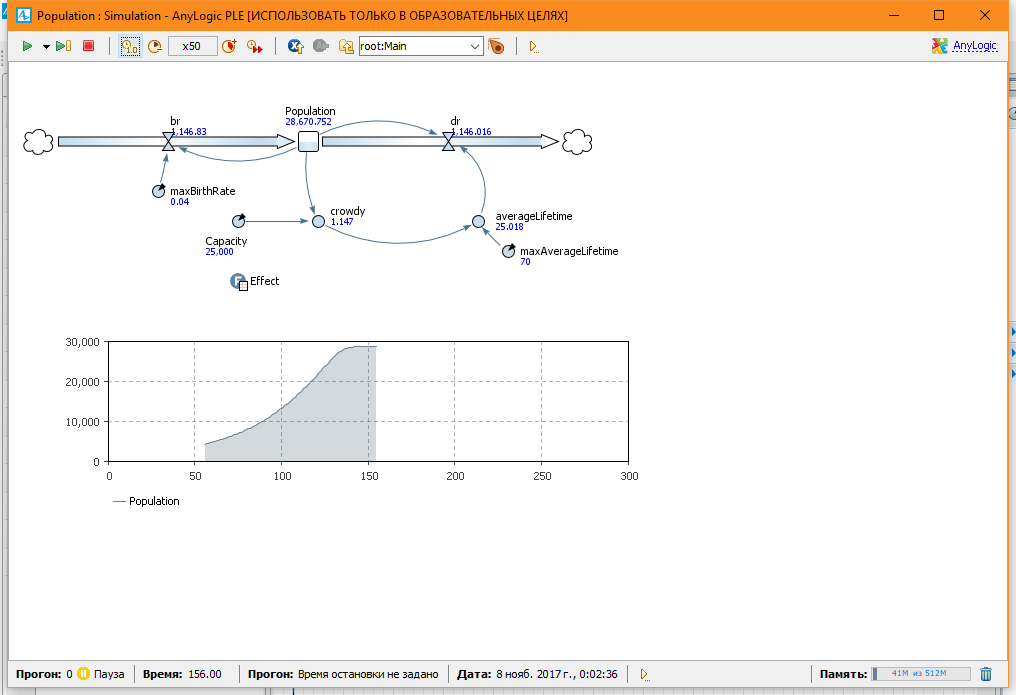
Модель 3. Ограниченный рост с задержкой.
В этой модели мы установили задержку для значения averageLifetime.
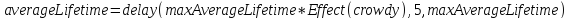
Где delay – Функция, которая задерживает заданный поток на указанное время.
Мы берем тот же поток, задаём ему задержку в 5 и начальными условиями ставим maxAverageLifetime.
При начальном населении в 10000 и capacity = 25000 наблюдаем следующую ситуацию.
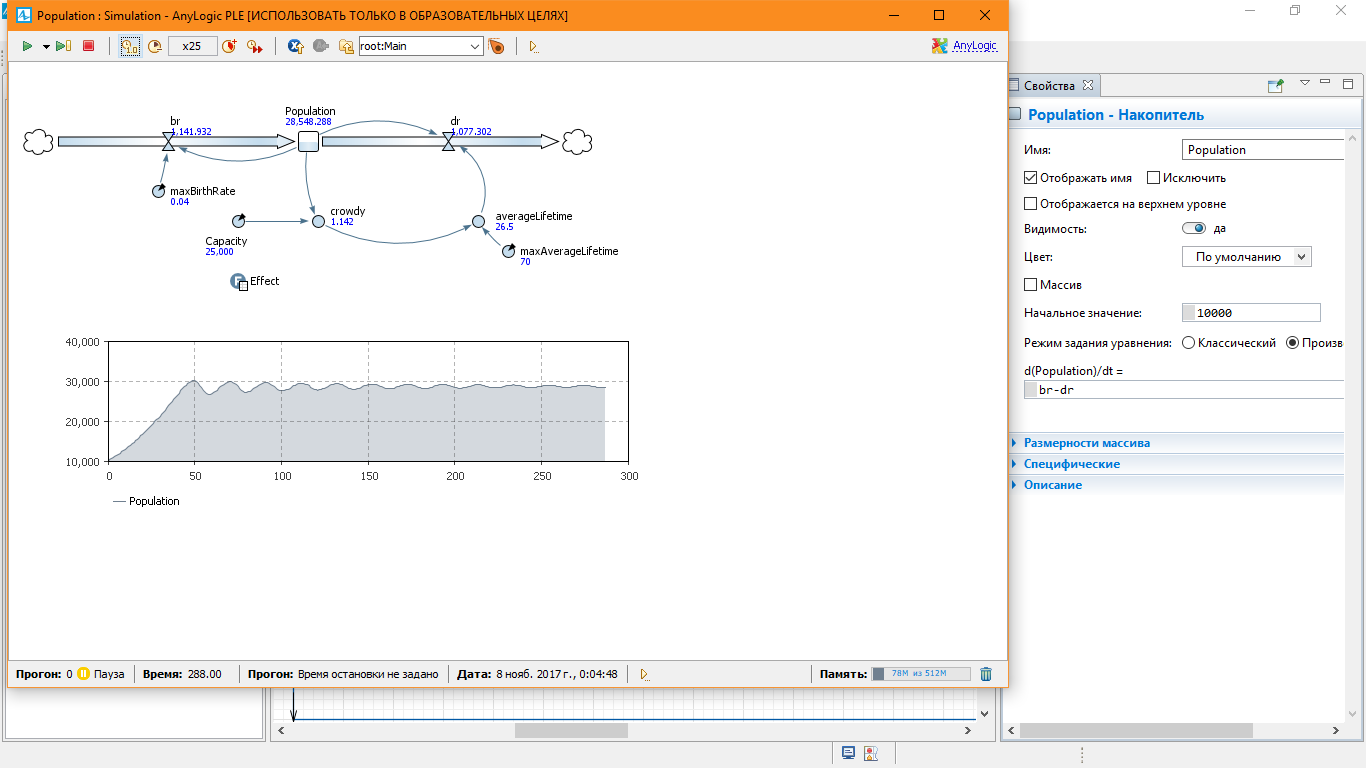
Модель 4. Непостоянность вместимости.
Мы модифицировали нашу модель, отразив в ней Capacity через поток. Теперь эта величина накопитель, и она меняется со временем.
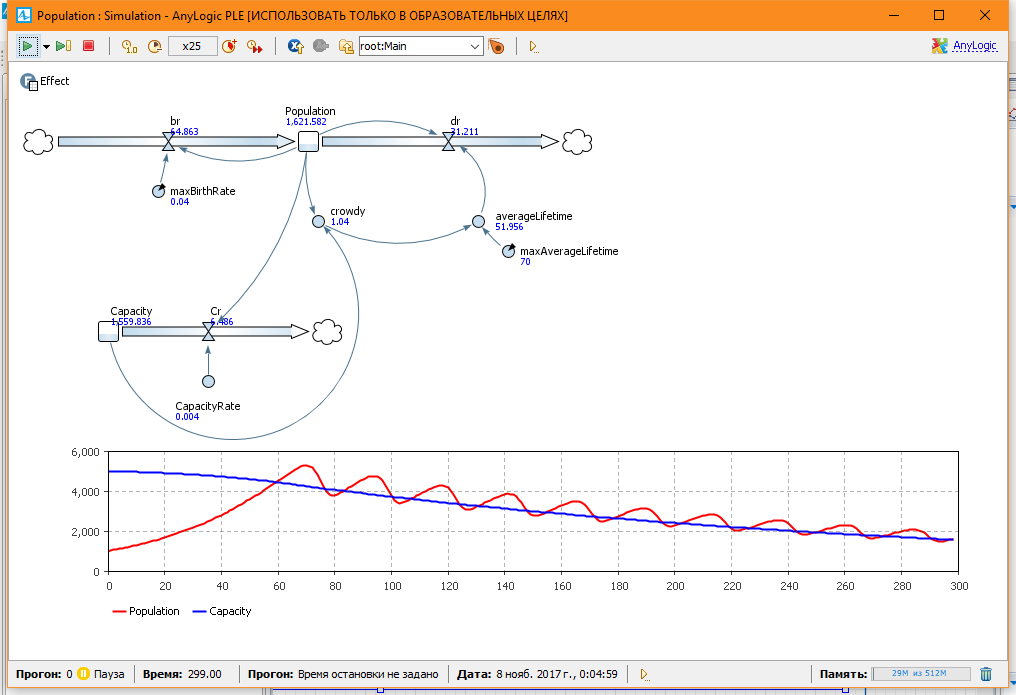
Начальные условия: Capacity = 5000, Population = 1000, CapacityRate = 0.004.
Выделим отдельно на временном графике Population и Capacity. Видим, как с уменьшением Capacity падает популяция.
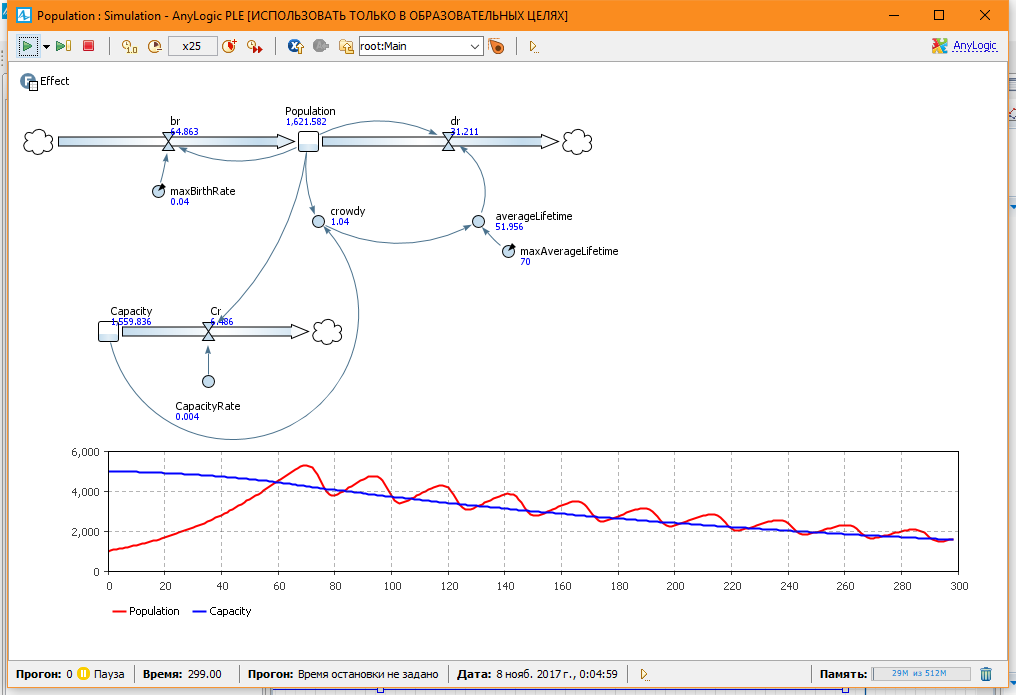
Санкт-Петербург 2017
