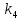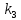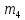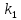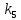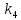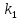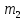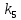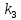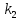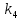контрольная / вариант 11

1. Раскрыть содержание теоретического вопроса (табл. 1). Виды первичных преобразований и их назначение.

Большинство первичных сообщений в системе управления непрерывны по множеству и по времени, и имеют различную природу (неэлектрическую) – звук, свет, давление, положение и т.д. С целью передачи по каналу связи сообщение преобразуется в условный электрический сигнал, который по своим параметрам и свойствам должен быть согласован с характеристикой данного канала связи с целью наилучшего прохождения по нему. Электрические сигналы аналогично сообщениям делятся на непрерывные (выражаются кривой тока) и дискретные (воспроизводятся электрическими импульсами, отличающимися разными формами).

Виды первичных преобразований сообщений:

• равномерное амплитудное квантование по уровню;

• неравномерное амплитудное квантование по уровню (с целью уменьшения среднеквадратичной ошибки);

• квантование по времени (лежит в основе импульсных и кодовых методов модуляции, многоканальных систем с ВРС);

• специальные виды преобразований (амплитудно-временное – Δ-преобразование- в системах с Δ-модуляцией; дифференциальное квантование; λΔ- преобразование).

Если из одного сигнала можно получить некоторую информацию о другом сигнале, то такие два сигнала называются когерентными (в когерентности выражается взаимная зависимость сигналов). Устранение избыточности в сообщении - декорреляция сигнала. Методы декорреляции: предсказание-вычитание, Δ-модуляция, укрупнение.

2. Используя алгоритмы эффективного кодирования информации Шеннона – Фено и Хаффмена, получить кодовые комбинации для передаваемых символов, вероятности появления которых приведены в табл. 2,3. Построить кодовое дерево.

Исходные данные алгоритма Шеннона – Фено:

Алгоритм построения кода:

1) все символы алфавита сообщений выписываются в порядке убывания вероятности их появления;

2) полученную ранжированную (упорядоченную) информацию последовательных символов разбивают на две группы так, чтобы суммы вероятностей в каждой группе были примерно равны;

3) всем знакам (символам) первой группы в качестве первого кодового символа присваивают значение 0, а для знака второй группы – значение 1;

4) полученные группы знаков снова разбиваются на 2 подгруппы по указанному выше принципу и вновь кодируют;

5) указанную процедуру продолжают, пока на очередном шаге в подгруппах не останется по одному знаку, верхнему последнему знаку присваивается символ 0, а нижнему – 1.

Таблица 1

Знаки	Вероятность	№ разбиения						Кодовые комбинации
		1	2	3	4	5
	1/2	0											1			1/2
	1/8	1	0	0			1						2			1/4
	1/8	1	0	1			1						2			1/4
	1/8	1	1	0			1		1				3			3/8
	1/32	1	1	1	0	0	1		1	1			4			1/8
	1/32	1	1	1	0	1	1		1	1			4			1/8
	1/32	1	1	1	1	0	1		1	1	1		5			5/32
	1/32	1	1	1	1	1	1		1	1	1	1	5			5/32			1,94

То есть, минимальная длина кодового слова 2 символа.

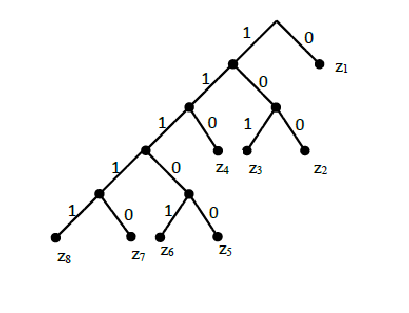
Кодовое дерево представлено на рисунке 1.

	0
	100
	101
	110
	11100
	11101
	11110
	11111

Рис. 1 Кодовое дерево Шеннона – Фено

Исходные данные алгоритма Хаффмена:

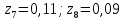
Алгоритм построения кода:

1) буквы (знаки) алфавита А а₁ а₂ а_n  располагают в порядке убывания их вероятностей P₁  P₂  P_n ;

2) два последних самых маловероятных знака или сообщения объединяют в одно вспомогательное сообщение с вероятностью равной сумме вероятностей этих знаков или сообщений Р_В  P_N1  P_N ;

3) полученный алфавит Aʹ=а₁ а₂ а_n-2 b с вероятностями P₁ P₂, …, P_b снова располагают в порядке убывания вероятностей;

4) снова отбирают два сообщения в новой полученной последовательности, имеющие наименьшую вероятность, объединяют их в одно сообщение и вычисляют их суммарную вероятность;

5) повторяют шаги п.1,2 до тех пор, пока не получат единственное сообщение, вероятность которого равна единице.

Кодовые комбинации для символов полученного алфавита z₁, z₂ ,…,z₈ образуются следующим образом. Символу ставится в соответствие код «0», если символ при объединении во вспомогательное сообщение занимает верхнее положение, и ставится код «1» – если символ занимает нижнее положение. Кодовые символы записывают при этом справа налево.

Таблица 2

Знаки	Вероятности	Вспомогательные столбцы
		1	2	3	4	5	6	7
	0,2	0,2	0,2	0,26	0,34	0,4	0,6	1
	0,18	0,18	0,2	0,2	0,26	0,34	0,4
	0,16	0,16	0,18	0,2	0,2	0,26
	0,12	0,14	0,16	0,18	0,2
	0,11	0,12	0,14	0,16
	0,09	0,11	0,12
	0,08	0,09
	0,06

Таблица 3

Символы алфавита	Код
	10
	000
	001
	011
	110
	111
	0100
	0101

Алгоритм построения кодового дерева: из точки, имеющей вероятность единица, направляют две ветви, причем ветви с наибольшей вероятностью присваивают символ 1, а с меньшей – 0. Такое последовательное ветвление продолжают, пока не дойдут до вероятности каждой буквы. Двигаясь по дереву, можно записать для каждой буквы её кодовую комбинацию.

Кодовое дерево представлено на рисунке 2.

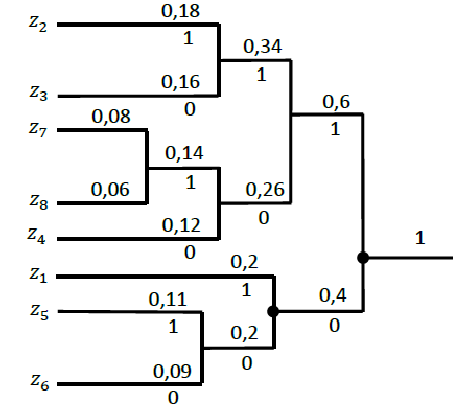
Рис. 2 Кодовое дерево Хаффмена

3. Используя алгоритм помехоустойчивого кодирования информации Хемминга, получить кодовую комбинацию для числа А. Предварительно перевести его в двоичную систему счисления. Осуществить декодирование числа В (варианты заданий даны в табл. 4). Сделать вывод о достоверности передачи (о наличии ошибки в принятой комбинации).

Исходные данные:

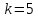следовательно количество информационных символов , а контрольных символов и размещаются они на позициях 1, 2, 4, 8, а информационные – на позициях 3, 5, 6, 7, 9. Эту последовательность в общем виде можно записать:

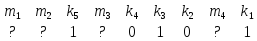(1)

Определение состава контрольных символов. Выявление того, какой

символ должен стоять на контрольной позиции (1 или 0), производится по

коэффициентам при помощи проверки на четность. В табл. 4 выписывают все кодовые комбинации (исключая нулевую) для пятиразрядного двоичного кода на все сочетания и рядом, справа, сверху вниз проставляют символы комбинации кода Хэмминга, записанные в последовательности (1).

Таблица 4

Разряды двоичных чисел					Символы кода
5()	4()	3()	2()	1()
0	0	0	0	1
0	0	0	1	0
0	0	0	1	1
0	0	1	0	0
0	0	1	0	1
0	0	1	1	0
0	0	1	1	1
0	1	0	0	0
0	1	0	0	1

Из таблицы 4 составляют таблицу 5, в которую выписывают символы в четыре строки в следующей закономерности. В первую строку таблицы 5 записываются те символы кода, против которых проставлены единицы в младшем (первом k₁) разряде комбинации двоичного кода в таблице 4. Во вторую строку проверочных коэффициентов (табл. 5) записываются символы кода, против которых стоит 1 во втором разряде (k₂) и т.д.

Таблица 5

Контрольные символы кода	Информационные символы кода

Нахождение состава контрольных символов при помощи проверок производится следующим образом. Суммируются информационные символы, входящие в каждую строку табл. 5. Если сумма единиц в данной строке четная, то значение символа , входящего в эту строку, равно 0, если нечетная, то –1.

Следовательно,

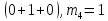. Таким образом кодовая комбинация числа .

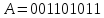Для проверки правильности принятого на приемной стороне кода (числа ) также используют метод проверки на четность. Для этого записывают число в виде:

Далее подставляют значения контрольных и информационных символов в таблицу 5, проверяют сумму строк на чётность и определяют искажённый помехой символ кода:

0 1 0 1 1 1

0 1 1 1 1

1 0 1 1 1

1 1 0

Сумма символов первой строки оказалась нечётной (1+1+1=0), поэтому для четности справа в первой строке приписываем 1. Сумма единиц во второй строке нечетная, поэтому справа для четности добавляем 1. Для получения четности третьей строки необходимо приписать 1. Сумма единиц в четвертой строке получилась четной, поэтому справа приписываем 0. Приписанные справа символы дали двоичное число 0111. Двоичное число 0111 означает десятичное число 7. Это значит, что искажение произошло в седьмом символе, считая слева направо, и символ кода 1 нужно исправить на 0. Так как позиции контрольных символов заранее известны, то после декодирования контрольные символы отбрасывают и получают переданную кодовую комбинацию, состоящую из одних информационных символов 10101. 1101₂ = 21₁₀. Можно сделать вывод, что одиночная ошибка при приеме исправлена, и сообщение принято без искажений.
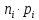
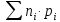
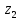
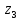
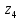
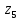
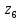
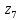
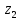
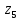
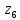
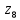
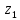
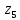
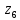
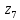
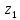
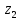
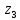
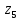
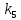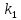