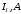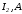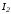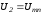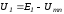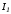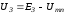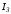- •Теоретические сведения к заданию 3 нелинейные электрические цепи постоянного тока
- •Параметры нелинейных резисторов
- •Методы расчета нелинейных электрических цепей постоянного тока
- •Графические методы расчета
- •Метод двух узлов
- •Алгоритм решения задачи
- •1. Выразим все токи в функции одного переменногонапряжения , для чего в соответствии с законом Ома для участка цепи с источником эдс запишемив функциии:
- •Расчет нелинейных цепей методом эквивалентного генератора
- •Аналитические методы расчета
- •Рассмотрим пример применения данного метода.
- •Нелинейные магнитные цепи при постоянных потоках Основные понятия и законы магнитных цепей
- •Характеристики ферромагнитных материалов
- •Магнитомягкие и магнитотвердые материалы
- •Статическая и дифференциальная магнитные проницаемости
- •Основные законы магнитных цепей
Метод двух узлов
Для цепей, содержащих два узла или сводящихся к таковым, можно применять метод двух узлов. При полностью графическом способе реализации метода он заключается в следующем.
Строятся графики зависимостей
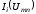 токов во всехi-х
ветвях в функции общей величины –
напряжения
токов во всехi-х
ветвях в функции общей величины –
напряжения
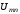 между узламиm
и n,
для чего каждая из исходных кривых
между узламиm
и n,
для чего каждая из исходных кривых
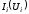 смещается вдоль оси напряжений
параллельно самой себе, чтобы ее начало
находилось в точке, соответствующей
ЭДС
смещается вдоль оси напряжений
параллельно самой себе, чтобы ее начало
находилось в точке, соответствующей
ЭДС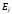 вi-й
ветви, а затем зеркально отражается
относительно перпендикуляра,
восстановленного в этой точке.
вi-й
ветви, а затем зеркально отражается
относительно перпендикуляра,
восстановленного в этой точке.Определяется, в какой точке графически реализуется первый закон Кирхгофа
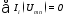 .
Соответствующие данной точке токи
являются решением задачи.
.
Соответствующие данной точке токи
являются решением задачи.
В качестве примера рассмотрим схему на рис. 3.14.
Симметричные
ВАХ нелинейных резисторов в схеме на
рис. 3.14 заданы в табл. 3.4. Найти токи в
ветвях схемы и напряжение
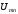 ,
если
,
если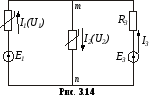
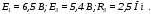
Таблица 3.4. ВАХ НР
|
|
0 |
0,5 |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
|
|
0 |
0,2 |
0,4 |
0,68 |
0,86 |
0,96 |
1,0 |
1,0 |
1,0 |
|
|
0 |
1,12 |
1,4 |
1,8 |
2,14 |
2,44 |
2,72 |
2,9 |
3,0 |
Алгоритм решения задачи
1. Выразим все токи в функции одного переменногонапряжения , для чего в соответствии с законом Ома для участка цепи с источником эдс запишемив функциии:
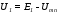 ;
(3.1)
;
(3.1)
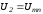 ;
(3.2)
;
(3.2)
 .
(3.3)
.
(3.3)
2. Задаваясь
различными значениями
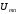 ,
на основании выражений (3.1)…(3.3) и данных
табл. 3.4 строим (см. рис. 3.15) графики
зависимостей
,
на основании выражений (3.1)…(3.3) и данных
табл. 3.4 строим (см. рис. 3.15) графики
зависимостей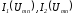 и
и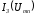 .
.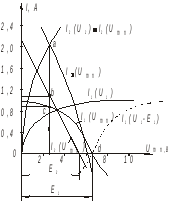
Рис.
3.15 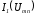 ,
то можно отметить следующее. Для точки
,
то можно отметить следующее. Для точки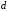
 и
и ;
следовательно,
;
следовательно,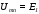 ,
т.е. начало кривой
,
т.е. начало кривой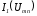 сдвинуто в точку
сдвинуто в точку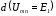 .
При этом кривая
.
При этом кривая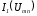 является зеркальным отображением кривой
является зеркальным отображением кривой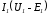 ,
получаемой путем переноса кривой
,
получаемой путем переноса кривой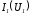 параллельно самой себе вдоль оси абсцисс
на отрезок
параллельно самой себе вдоль оси абсцисс
на отрезок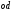 .
На основании изложенного на практике
кривая зависимости
.
На основании изложенного на практике
кривая зависимости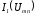 строится в соответствии с приведенной
выше методикой:
строится в соответствии с приведенной
выше методикой:
смещаем
кривую
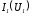 вдоль оси абсцисс параллельно самой
себе так, чтобы ее начало находилось в
точке
вдоль оси абсцисс параллельно самой
себе так, чтобы ее начало находилось в
точке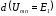 (см. пунктирную кривую
(см. пунктирную кривую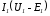 на рис. 3.15);
на рис. 3.15);
проводим
через точку
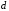 ортогональ и зеркально отражаем
относительно ее пунктирную кривую
ортогональ и зеркально отражаем
относительно ее пунктирную кривую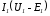
получаем кривую
получаем кривую
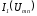 .
.
Аналогично
строится зависимость
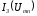 .Поскольку средняя ветвь не содержит
источника ЭДС, кривая
.Поскольку средняя ветвь не содержит
источника ЭДС, кривая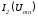 тождественна кривой
тождественна кривой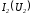 .
.
3.
Строим кривую
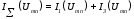 .
.
4. Поскольку
в соответствии с первым законом Кирхгофа
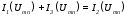 ,
точка
,
точка пересечения кривых
пересечения кривых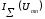 и
и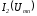 определяет рабочий режим цепи. Проекция
точки
определяет рабочий режим цепи. Проекция
точки на ось ординат соответствует току во
второй ветви:
на ось ординат соответствует току во
второй ветви: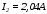 .
Проекции точки
.
Проекции точки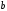 и
и пересечения перпендикуляра, опущенного
из точки
пересечения перпендикуляра, опущенного
из точки ,
с графиками зависимостей
,
с графиками зависимостей и
и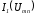 на ось ординат определяют соответственно
токи
на ось ординат определяют соответственно
токи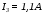 и
и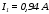 .
.
5.
Искомому напряжению соответствует
проекция точки
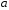 на ось абсцисс, т.е.
на ось абсцисс, т.е. .
.
Метод двух узлов может быть реализован и в другом варианте, отличающемся от изложенного выше меньшим числом графических построений.
В качестве примера рассмотрим цепь на рис. 3.14.
Задаемся
током, протекающим через один из
резисторов, например во второй ветви
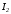 ,
и рассчитываем
,
и рассчитываем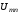 ,
а затем по
,
а затем по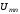 с использованием (3.1) и (3.3) находим
с использованием (3.1) и (3.3) находим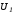 и
и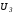 и по зависимостям
и по зависимостям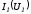 и
и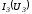
соответствующие им токи
соответствующие им токи
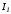 и
и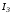 и т.д. Результаты вычислений сводим в
табл. 3.5, в последней колонке которой
определяем сумму токов:
и т.д. Результаты вычислений сводим в
табл. 3.5, в последней колонке которой
определяем сумму токов:
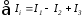 .
.
Таблица 3.5. Таблица результатов расчета методом двух узлов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгебраическая
сумма токов в соответствии с первым
законом Кирхгофа должна равняться нулю,
поэтому получающаяся в последней колонке
табл. 3.5 величина
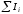 указывает, каким значением
указывает, каким значением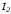 следует задаваться на следующем шаге.
следует задаваться на следующем шаге.
В
осях
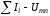 строим кривую зависимости
строим кривую зависимости и по точке ее пересечения с осью напряжений
определяем напряжение
и по точке ее пересечения с осью напряжений
определяем напряжение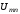 между точкамиm
и n.
Для найденного значения
между точкамиm
и n.
Для найденного значения
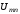 по (3.1)…(3.3) рассчитываем напряжения на
резисторах, после чего по заданным
зависимостям
по (3.1)…(3.3) рассчитываем напряжения на
резисторах, после чего по заданным
зависимостям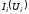 определяем токи в ветвях схемы.
определяем токи в ветвях схемы.