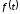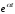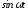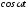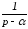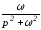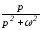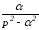Переходные процессы при подключении последовательной

R–L–C-цепи к источнику напряжения

Рассмотрим два случая:

а) ;

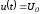б) .

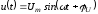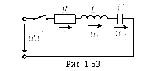
Согласно изложенной выше методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 1.53 можно записать

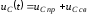. (1.13)

Тогда для первого случая принужденная составляющая этого напряжения

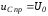. (1.14)

Характеристическое уравнение цепи имеет вид

,

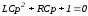решая его, получаем

.

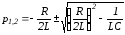В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:

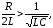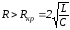1. или, где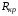–критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.

В этом случае

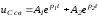. (1.15)

2. 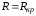– предельный случай апериодического режима.

В этом случае 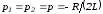и

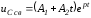. (1.16)

3. 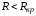– периодический (колебательный) характер переходного процесса.

В этом случае 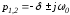и

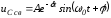, (1.17)

где – коэффициент затухания;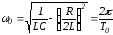–угловая частота собственных колебаний; 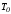– период собственных колебаний.

Для апериодического характера переходного процесса после подстановки (1.14) и (1.15) в соотношение (1.13) можно записать

.

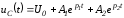Для нахождения постоянных интегрирования, учитывая, что в общем случае 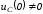и в соответствии с первым законом коммутации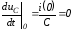, запишем дляt=0 два уравнения:

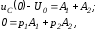
решая которые, получим

; .

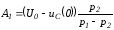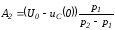Таким образом,

.

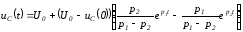Тогда ток в цепи

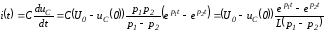
и напряжение на катушке индуктивности

.

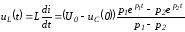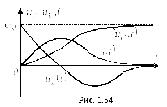
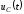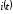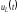На рис. 1.54 представлены качественные кривые ,и, соответствующие апериодическому переходному процессу при.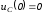

Для критического режима на основании (1.14) и (1.16) можно записать:

.

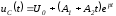При

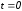
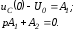
Таким образом,

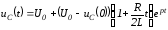
и

.

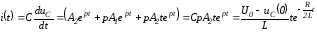Для колебательного переходного процесса в соответствии с (1.14) и (1.17) имеем

.

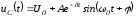Для нахождения постоянных интегрирования запишем

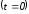
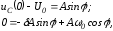
откуда 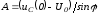и.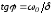

Тогда

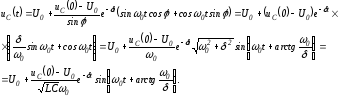
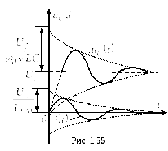
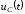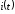На рис. 1.55 представлены качественные кривые и, соответствующие колебательному переходному процессу при.

При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым

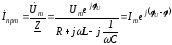и

,

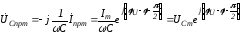где ;;.

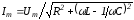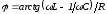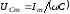Таким образом,

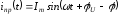и .

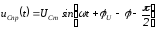Здесь также возможны три режима:

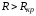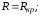1. ; 2.3.

. ..

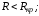
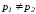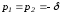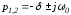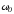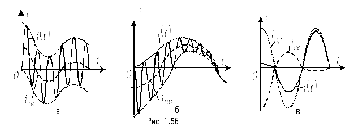
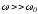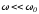Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 –; 2 –; 3 –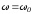, – которые представлены на рис. 1.56,а,б,в соответственно.

ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

Сущность операторного метода заключается в том, что функции 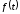вещественной переменнойt, которую называют оригиналом, ставится в соответствие функция 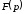комплексной переменной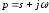, которую называютизображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что, в свою очередь, определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.

Изображение 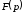заданной функции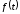определяется в соответствии спрямым преобразованием Лапласа:

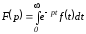. (1.18)

В сокращенной записи соответствие между изображением и оригиналом обозначается как

или .

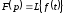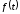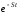Следует отметить, что если оригинал увеличивается с ростомt, то для сходимости интеграла (1.18) необходимо более быстрое убывание модуля . Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.

В качестве примера в табл. 1.6 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.

Таблица 1.6. Изображения типовых функций

Оригинал	А
Изображение