
- •Теоретические сведения к заданию 1
- •Классический метод расчета переходных процессов
- •Для последовательной цепи, содержащей линейные резистор r, катушку индуктивности l и конденсатор с, при ее подключении к источнику с напряжением u (см. Рис. 1.41) можно записать
- •Подставив в (1.1) значение тока через конденсатор
- •В общем случае уравнение, описывающее переходный процесс в цепи с nнезависимыми накопителями энергии, имеет вид
- •Начальные условия. Законы коммутации
- •Общая методика расчета переходных процессов классическим методом
- •Примеры расчета переходных процессов классическим методом
- •1. Переходные процессы в r-l-цепи при ее подключении к источнику напряжения
- •2. Переходные процессы при отключении катушки индуктивности от источника питания
- •3. Заряд и разряд конденсатора
- •Энергии и произвольным числом резисторов
- •Переходные процессы при подключении последовательной
- •В этом случае
- •Некоторые свойства изображений
- •Изображения производной и интеграла
- •Закон Ома в операторной форме
- •Для мгновенных значений переменных можно записать:
- •Законы Кирхгофа в операторной форме Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю:
- •Переход от изображений к оригиналам
- •Например, для изображения тока в цепи на рис. 1.61 можно записать:
- •Последовательность расчета переходных процессов операторным методом
- •Формулы включения
- •В результате
- •Сведение расчета переходного процесса к расчету с нулевыми начальными условиями
- •Метод переменных состояния
- •Методика составления уравнений состояния на основе принципа наложения
- •Решение
- •Решение
- •Решение
Общая методика расчета переходных процессов классическим методом
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
Запись выражения для искомой переменной в виде
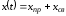 .
(1.6)
.
(1.6)
Нахождение принужденной составляющей общего решения на основании расчета установившегося режима послекоммутационной цепи.
Составление характеристического уравнения и определение его корней (для цепей, описываемых дифференциальными уравнениями первого порядка, вместо корней можно находить постоянную времени – см. далее). Запись выражения свободной составляющей в форме, определяемой типом найденных корней.
Подстановка полученных выражений принужденной и свободной составляющих в соотношение (1.6).
Определение начальных условий и на их основе – постоянных интегрирования.
Примеры расчета переходных процессов классическим методом
1. Переходные процессы в r-l-цепи при ее подключении к источнику напряжения
Такие процессы имеют место, например,
при подключении к источнику питания
электромагнитов, трансформаторов,
электрических двигателей и т.п.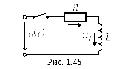
Рассмотрим два случая:
а)
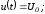
б)
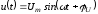 .
.
Согласно рассмотренной методике для тока в цепи на рис. 1.45 можно записать
 .
(1.7)
.
(1.7)
Тогда для первого случая принужденная составляющая тока
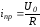 .
(1.8)
.
(1.8)
Характеристическое уравнение имеет вид
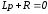 ,
,
откуда
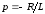 и постоянная времени
и постоянная времени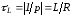 .
.
Таким образом,
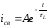 .
(1.9)
.
(1.9)
Подставляя (1.8) и (1.9) в соотношение (1.7), запишем:
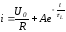 .
.
В соответствии с первым законом
коммутации
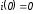 .
Тогда
.
Тогда
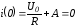 ,
,
откуда
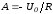 .
.
Таким образом, ток в цепи в переходном процессе описывается уравнением
 ,
,
а
напряжение на катушке индуктивности –
выражением 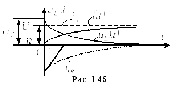
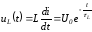 .
.
Качественный вид кривых
 и
и ,
соответствующих полученным решениям,
представлен на рис. 1.46.
,
соответствующих полученным решениям,
представлен на рис. 1.46.
При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:
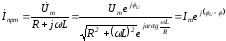 ,
,
где
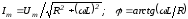 .
.
Отсюда
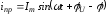 .
.
Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,
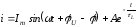 .
.
Поскольку
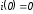 ,
то
,
то
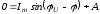 .
.
Таким образом, окончательно получаем
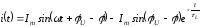 .
(1.10)
.
(1.10)
Анализ полученного выражения (1.10) показывает следующее.
При начальной фазе напряжения
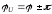 постоянная интегрированияА=0.
Таким образом, в этом случае коммутация
не повлечет за собой переходного
процесса и в цепи сразу возникнет
установившийся режим.
постоянная интегрированияА=0.
Таким образом, в этом случае коммутация
не повлечет за собой переходного
процесса и в цепи сразу возникнет
установившийся режим.При
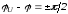 свободная составляющая максимальна
по модулю. В этом случае ток переходного
процесса достигает своей наибольшей
величины.
свободная составляющая максимальна
по модулю. В этом случае ток переходного
процесса достигает своей наибольшей
величины.
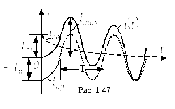
Если
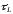 значительна по величине, то за полпериода
свободная составляющая существенно не
уменьшается. В этом случае максимальная
величина тока переходного процесса
значительна по величине, то за полпериода
свободная составляющая существенно не
уменьшается. В этом случае максимальная
величина тока переходного процесса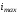 может существенно превышать амплитуду
тока установившегося режима. Как видно
из рис. 1.47, где
может существенно превышать амплитуду
тока установившегося режима. Как видно
из рис. 1.47, где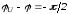 ,
максимум тока имеет место примерно
через
,
максимум тока имеет место примерно
через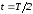 .
В пределе при
.
В пределе при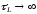
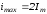 .
.
Таким образом, для линейной цепи
максимальное значение тока переходного
режима не может превышать удвоенной
амплитуды принужденного тока:
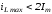 .
.
Аналогично для линейной цепи с
конденсатором: если в момент коммутации
принужденное напряжение равно своему
амплитудному значению и постоянная
времени
 цепи достаточно велика, то примерно
через половину периода напряжение на
конденсаторе достигает своего
максимального значения
цепи достаточно велика, то примерно
через половину периода напряжение на
конденсаторе достигает своего
максимального значения ,
которое не может превышать удвоенной
амплитуды принужденного напряжения:
,
которое не может превышать удвоенной
амплитуды принужденного напряжения: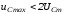 .
.
