27.Ротор вектора и его основные свойства.

Ротором векторного поля ā (M) = P (x;y;z ) i+ Q (x;y;z ) j+ R (x;y;z ) k называется вектор []

ОБОЗНАЧАЮТ: rot ā (M)

ФИЗИЧЕСКИЙ СМЫСЛ РОТОРА Вектор rot ā (M) указывает направление, ортогонально которому вращательная способность поля наибольшая.

СВОЙСТВА РОТОРА 1) Если ā (M) = const, то rot ā (M) = 0̄;

2) Если C1,C2 – const, то rot( С1ā1 + С2 ā 2 ) = С1rot ā 1+ С2rot ā2 ;

3) Если u = u (x,y,z) = u (M) , то rot[ u (M) · ā (M)]= u (M) · rot ā (M) +[grad u (M) , ā (M)] ;

4) rot(grad u) = 0̄; 5) div(rot ā) = 0 .

28. Оператор Гамильтона. Векторные дифференциальные операции 1-го и 2-го порядков.

-называется оператором Гамильтона и обозначается символом

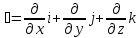
Дифференциальная операция 1-го порядка:

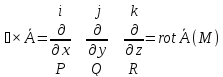
Дифференциальная операция 2-го порядка:

29. Сходимость и расходимость числового ряда.

Числовой ряд – это сумма членов числовой последовательности вида .

Ряд называется сходящимся если его n-я частичная сумма при неограниченном возрастании n стремится к конечному пределу т.е. если существует конечный предел.

Конечный предел частичных сумм при n-> бесконечности назыв. суммой ряда.

Если , или не существует, то ряд называется расходящимся и суммы не имеет.

30.Геометрическая прогрессия и случаи ее сходимости и расходимости.

Последовательность чисел {an} называется геометрической прогрессией, если отношение последующего члена к предыдущему равно одному и тому же постоянному числу q, называемому знаменателем геометрической прогрессии. Таким образом, для всех членов геометрической прогрессии. Предполагается, что q≠0 и q≠1.

Сумма первых n членов геометрической прогрессии определяется выражением

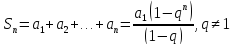
31.Необходимый признак сходимости ряда.

Необходимый признак сходимости числовых рядов имеет простую формулировку: общий член сходящегося ряда стремится к нулю. Можно записать этот признак и более формально:

Доказать: Рассмотрим ряд

По условию ряд сходится

Запишем ряд в виде U₁+U₂+U₃+…+U_n-1+U_n+…

Вычтем из равенства (1) равенство (2) по членно следовательно

Если общий член ряда не стремится к нулю при n->то ряд расходится еслито ряд может сходится может расходится.

32. Гармонический ряд и доказательство его расходимости.

- Гармонический ряд.

Докажем что гармонический ряд расходится воспользуемся неравенством

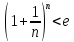
Прологарифмируем nln(1+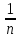)<lne

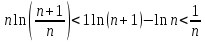
Это неравенство справедливо при любом n.

Будем придавать последовательно значения равными 1,2,3,…,n

Сложим левую и правую части неравенств, в правой части стоит n-я частичная сумма гармонического ряда Следовательно пределS_n равен ряд расходится.

33. Свойства сходящихся рядов.

1. (Линейность суммы ряда).

2. Если в сходящемся ряде ввести парные скобки, то сумма ряда не изменится. Отбрасывать скобки, вообще говоря, нельзя.

3. Если произвести перестановку, затрагивающую конечное число членов ряда, то это не повлияет ни на сходимость, ни на сумму ряда. Это уже не верно для бесконечных перестановок членов ряда.

34. Достаточные признаки сходимости знакоположительных рядов

I. Признак сравнения. Пусть заданы два ряда: a₁+a₂+...+a_n+...=_(n=1)∑^∞ a_n b₁+b₂+...+b_n+...=_(n=1)∑^∞ b_n Если для любого i выполняется a_i≥b_i, то ряд _(n=1)∑^∞ a_n называется мажорантным по отношению к ряду _(n=1)∑^∞ b_n, а ряд _(n=1)∑^∞ b_n - минорантным по отношению к _(n=1)∑^∞ a_n. Теорема(1): Если мажорантный ряд сходится, то и минорантный ряд также сходится.

Теорема(2) (достаточный признак расходимости): Если минорантный ряд расходится, то и мажорантный к нему ряд также расходится.

Замечание: Признак сравнения даёт ответ только в двух случаях из четырёх возможных при работе с двумя рядами. Чтобы сравнивать ряды необходимо иметь такие ряды для сравнения, про которые заранее известно о их сходимости или расходимости. К самым популярным из них относятся: 1. Ряды, составленные из членов геометрической прогрессии, про которые известно, что при |q|<1 они сходятся, а при |q|≥1 - расходятся. 2. Обобщённые гармонические ряды (_(n=1)∑^∞ 1/n^α), которые сходятся при α>1 и расходятся при α≤1. Особо стоит отметить гармонический ряд при α=1, который является расходящимся!

II. Признак д'Аламбера. Теорема: Если в ряде с положительными членами отношение (n+1)-го члена (а_n+1) к a_n при n→∞ имеет конечный предел, т.е. lim (а_n+1/а_n)=l<∞, то, в зависимости от значения предела l, доказано следующее: 1) l<1 - ряд сходится; 2) l>1 - ряд расходится; 3) l=1 - результат не определён.

III. Интегральный признак Коши Если члены знакоположительного ряда не возрастают, то вопрос о сходимости или расходимости ряда может быть решён с помощью так называемой "производной функции", где f(1)=a₁, f(2)=a₂, ..., f(n)=a_n. При этом, если ₁∫^+∞ f(x)dx - сходится, то ряд также сходится, а если ₁∫^+∞ f(x)dx - расходится, то и ряд - расходится.

Радикальный признак Коши используется для исследования сходимости рядов, общий член которых является неотрицательным, т.е. un≥0. Такие ряды называют положительными. В стандартных примерах радикальный признак Коши используют в предельной форме.

Радикальный признак Коши (в предельной форме)

Если ряд ∑n=1∞un положителен и

limn→∞un−−√n=L,

то при L<1 ряд сходится, а при L>1 (и при L=∞) ряд расходится.