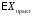Выводы.
В ходе выполнения практического задания были повторены свойства и способы построения случайной величины, а также получены навыки моделирования случайных величин. Результатом работы стали смоделированные равномерная, показательная и треугольная случайные величины на основе стандартной равномерной случайной величины. Были найдены экспериментальные значения математического ожидания, дисперсии и СКО для каждой величины. В ходе анализа полученных данных было установлено, что с ростом объёма выборки экспериментальное значение стремится к теоретическому значению величины, особенно это хорошо наблюдается для треугольного распределения.
Таблица 2 – Исследуемые величины для равномерного, экспоненциального и треугольного распределений
|
Распределение |
N |
|
|
|
|
|
|
σпракт |
σтеор |
∆σ |
|
|
100 |
39.7694 |
40 |
0.2306 |
526.5138 |
533.3333 |
6.8195 |
22.9459 |
23.0940 |
0.1481 |
|
500 |
40.8304 |
0.8304 |
552.9137 |
19.5804 |
23.5141 |
0.4201 |
||||
|
1000 |
40.9087 |
0.9087 |
521.1683 |
12.1650 |
22.8291 |
0.2649 |
||||
|
10000 |
40.0448 |
0.0448 |
535.1502 |
1.8169 |
23.1333 |
0.0393 |
||||
|
|
100 |
39.9502 |
40 |
0.0498 |
1538.4024 |
1600 |
61.5976 |
39.2225 |
40 |
0.7775 |
|
500 |
38.0347 |
1.9653 |
1301.2349 |
298.7651 |
36.0726 |
3.9274 |
||||
|
1000 |
38.4725 |
1.5275 |
1514.1333 |
85.8667 |
38.9119 |
1.0881 |
||||
|
10000 |
40.1030 |
0.1030 |
1636.3893 |
36.3893 |
40.4523 |
0.4523 |
||||
|
|
100 |
3.2980 |
3.3333 |
0.0354 |
5.4251 |
5.5556 |
0.1304 |
2.3292 |
2.3570 |
0.0278 |
|
500 |
3.4415 |
0.1082 |
5.9602 |
0.4047 |
2.4414 |
0.0843 |
||||
|
1000 |
3.4077 |
0.0743 |
5.4112 |
0.1443 |
2.3262 |
0.0308 |
||||
|
10000 |
3.3356 |
0.0022 |
5.5298 |
0.0258 |
2.3515 |
0.0054 |
Приложение а реализация программы, Генерирующая последовательности случайных чисел
alpha <- 80; lambda <- .025; A <- 10
N <- 1000
# U ~ U(0;1)
U <- runif(N)
# X1 ~ U(0; alpha)
X1 <- alpha * U
hist(X1)
# X2 ~ Exp(0, lambda)
X2 <- -log(U) / lambda
hist(X2)
# X3 ~ Tr(a, b, c)
a <- c <- 0; b <- A
X3 <- b - sqrt((1 - U) * (b - a) * (b - c))
hist(X3)
# Создание таблицы
distribution <- c("U(0, alpha)", "Exp(0, lambda)", "Tr(a, b, c)")
sample.size <- rep(N, 3)
mean.exper <- c(mean(X1), mean(X2), mean(X3))
mean.theor <- c(alpha / 2, 1 / lambda, (a + b + c) / 3)
var.exper <- c(var(X1), var(X2), var(X3))
var.theor <- c(alpha ^ 2 / 12,
1 / lambda ^ 2,
(a ^ 2 + b ^ 2 + c ^ 2 - a * b - a * c - b * c) / 18)
sigma.exper <- c(sd(X1), sd(X2), sd(X3))
sigma.theor <- c(alpha / sqrt(12),
1 / lambda,
sqrt(a ^ 2 + b ^ 2 + c ^ 2 - a * b - a * c - b * c) / sqrt(18))
delta.mean <- abs(mean.exper - mean.theor)
delta.var <- abs(var.exper - var.theor)
delta.sigma <- abs(sigma.exper - sigma.theor)
data.base <- data.frame(distribution,
sample.size,
mean.exper,
mean.theor,
delta.mean,
var.exper,
var.theor,
delta.var,
sigma.exper,
sigma.theor,
delta.sigma)
View(data.base)
Приложение Б
Гистограммы для равномерного распределения
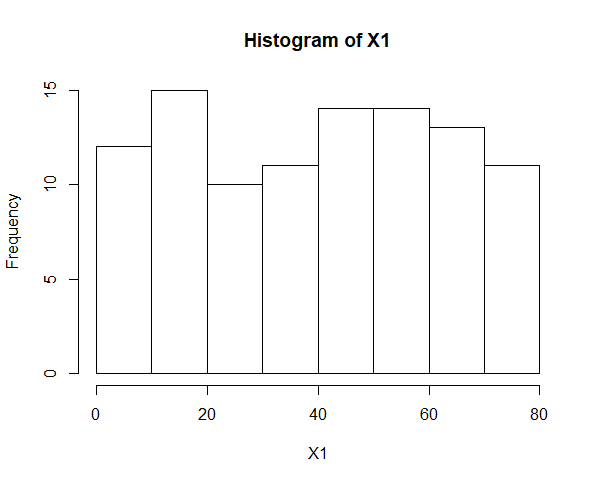
Рисунок 1 – Гистограмма для равномерного распределения при объёме выборки 100

Рисунок 2 – Гистограмма для равномерного распределения при объёме выборки 500

Рисунок 3 – Гистограмма для равномерного распределения при объёме выборки 1000

Рисунок 3 – Гистограмма для равномерного распределения при объёме выборки 10000
Приложение В
Гистограммы для Показательного распределения

Рисунок 5 – Гистограмма для показательного распределения при объёме выборки 100

Рисунок 6 – Гистограмма для показательного распределения при объёме выборки 500

Рисунок 7 – Гистограмма для показательного распределения при объёме выборки 1000

Рисунок 8 – Гистограмма для показательного распределения при объёме выборки 10000
Приложение Г
Гистограммы для Треугольного распределения

Рисунок 9 – Гистограмма для треугольного распределения при объёме выборки 100

Рисунок 10 – Гистограмма для треугольного распределения при объёме выборки 500

Рисунок 11 – Гистограмма для треугольного распределения при объёме выборки 1000

Рисунок 12 – Гистограмма для треугольного распределения при объёме выборки 10000