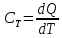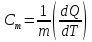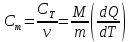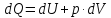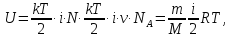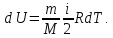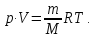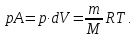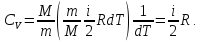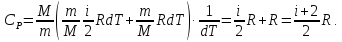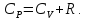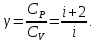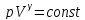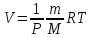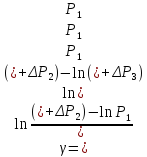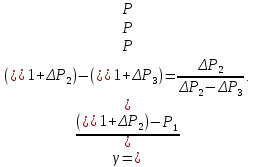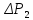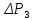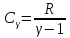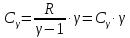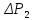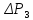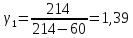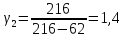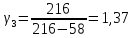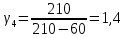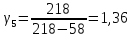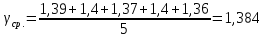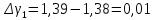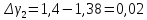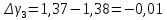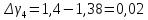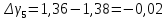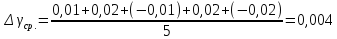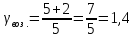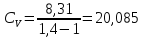Лабораторная работа №11 (готовая)

Липецкий государственный технический университет

Кафедра Физики и Биомедицинской техники

ЛАБОРАТОРНАЯ РАБОТА № 11

физике

наименование дисциплины

по

ОПРЕДЕЛЕНИЕ МОЛЯРНЫХ ТЕПЛОЁМКОСТЕЙ ГАЗОВ

название темы

подпись	ФИО

Студент:

Группа:

учёная степень	подпись	ФИО

Руководитель:

Липецк 2017 г.

Цель работы: изучение особенностей адиабатического процесса и определение молекулярных теплоёмкостей воздуха.

Приборы и принадлежности: баллон, насос-«груша», манометр для измерения разности давлений в баллоне и в атмосфере, кран, зажим, соединительные шланги.

Теплоемкостью тела 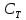называется количество теплоты, необходимое для нагревания тела на один кельвин (К):

(1)

Удельная теплоемкость ­– величина, равная количеству теплоты, необходимому для нагревания единицы массы вещества на один кельвин:

(2)

Молярная теплоемкость равна количеству теплоты, необходимому для нагревания одного моля вещества на один кельвин:

(3)

где М — масса одного моля, dQ - количество теплоты, необходимое для

увеличения температуры вещества массой m на dT Кельвин, 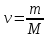- количество вещества (в молях).

Согласно первому началу термодинамики количество теплоты dQ, подводимое к системе, расходуется на приращение внутренней энергии системы dU и на совершение системой работы dA=p·dV против внешних сил: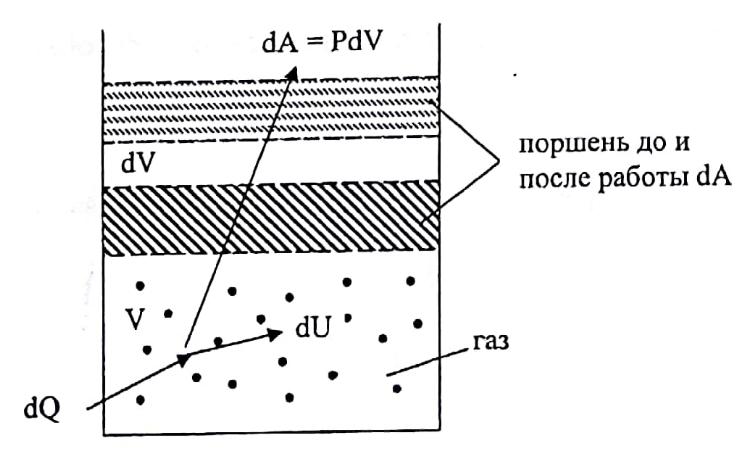

(4)

Где p – давление, dU – приращение объема системы (рис. 1).

Внутренняя энергия идеального газа равна средней кинетической энергии ε = кТ/2, приходящейся на одну степень свободы молекулы, умноженной на число степенной свободы (і·N) всех N молекул газа в данном количестве вещества:

(5)

где 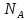– число Авогадро; K – постоянная Больцмана; 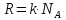– универсальная газовая постоянная; m/M = N/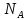 – число молей вещества, і – число степеней свободы одной молекулы, равное наименьшему числу независимых координат, которые необходимо указать, чтобы определить положение молекулы в пространстве. Другое определение: і – это число независимых движений, в которых одновременно может участвовать тело. Из формулы (5) следует, что приращение внутренней энергии выражается формулой (6)

(6)

Из уравнения состояния идеального газа

(7)

получим выражение работы при расширении идеального газа на dV при P=const.

(8)

Молярная теплоемкость газа зависит от условий его нагревания. При изохорическом процессе (V=const) dV=0, следовательно dA=0, поэтому с учетом уравнения (4), (6) и (3) найдем

(9)

При изобарическом процессе (p=const), используя уравнения (4), (6), (8) и (3), получим

(10)

Из формул (9) и (10) следует связь между молярными теплоемкостями (уравнение Майера)

(11)

С учетом (8) можно показать, что R равна работе 1-го моля идеального газа при его нагревании на 1 К в изобарном процессе. Из (11) следует, что 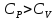‚ так как в изобарном процессе часть тепла расходуется на совершение газом работы‚ а в изохорном процессе работа газом не совершается.

Экспериментальное определение молярных теплоемкосте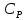й , и 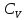по формуле (3) затруднено тем, что масса газа обычно очень мала по сравнению с массой сосуда, в которой он находится. Поэтому из опыта находят отношение

теплоемкостей, которое с учетом формул (9) и (10) равно:

(12)

МЕТОДИКА ИЗМЕРЕНИЙ

Экспериментальная установка состоит из баллона (1), насоса-«груши» (2), манометра (3), тройника (4), зажима (5), соединительных трубок (6) и (7), клапана (8).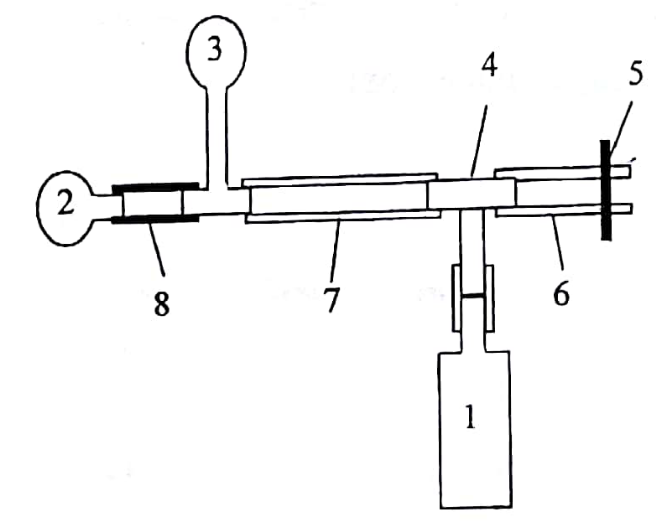

Исходное состояние газа в баллоне характеризуется параметрами 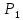V, ,

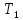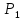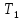где V – объем баллона, и – давление и температура воздуха в лаборатории. Измерения проводятся в 3 этапа.

1. Зажимом (5) пережимают шланг (6). Насосом-«грушей» создают в системе избыточное давление 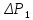в результате состояние системы характеризуется параметрами 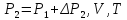. Следует отметить, что при накачке температура газа несколько повышается, а после прекращения накачки температура газа и его давление в системе несколько снижаются.

2. После стабилизации температуры и давления открывают шланг (6), соединяющий систему с атмосферой, и давление в системе выравнивается с атмосферным. Соединение баллона с атмосферой может быть также осуществлено поворотом клапана (8) на насосе-груше (2).

Процесс выравнивания давлений идет достаточно быстро, теплообмен с окружающей средой не успевает произойти, и этот процесс можно считать адиабатическим. Состояние газа в конце этого процесса характеризуется параметрами 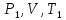. Поскольку работа расли/трения газа совершается за счет уменьшения его внутренней энергии, .

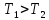3. Сразу после выравнивания давлений отсоединяют систему (баллон) от атмосферы, используя зажим (5) или клапан (8). После этого происходит медленное изохорное нагревание воздуха со скоростью, определяемой теплопроводностью стенок баллона и других частей системы. Нагрев воздуха происходит до комнатной температуры 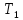и сопровождается повышением давления до величины 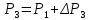. Величина 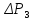– это новое избыточное давление (по сравнению с атмосферным), определяемое экспериментально.

Далее рассмотрим газовые законы для двух процессов:

6) адиабатного

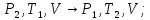
в) изохорного

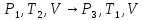
Адиабатический процесс расширения воздуха характеризуется уравнением

Пуассона (этап б):

(13)

Используя уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) (7), находим

(14)

Используя (13) и (14), можно исключить из рассмотрения неизвестный объём V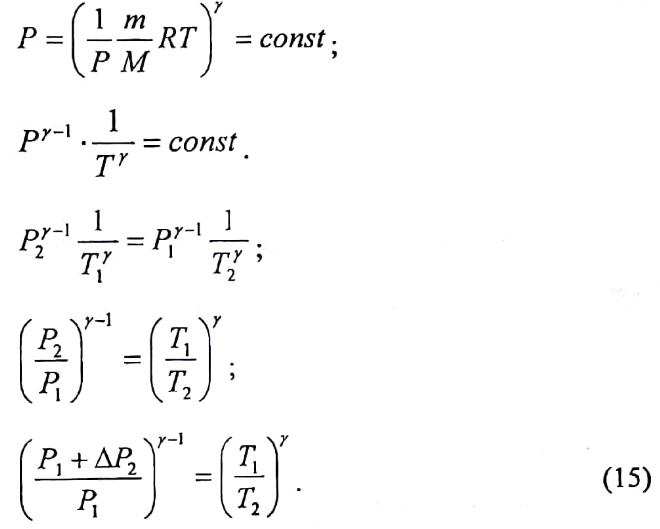

Изохорный процесс выравнивания температуры воздуха в баллоне и лаборатории при закрытом зажиме 5 подчиняется закону Шарля (этап в):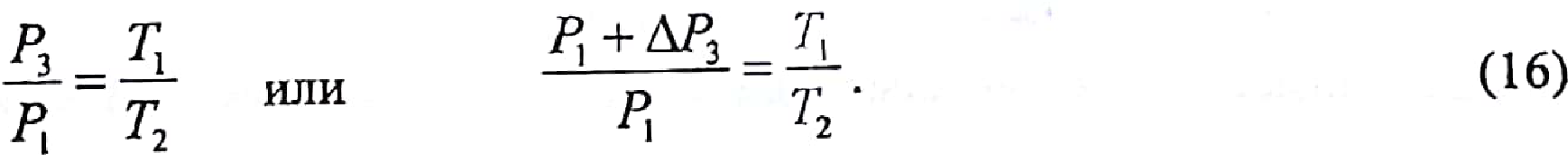

Исключив из уравнений (15) и (16) 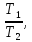получим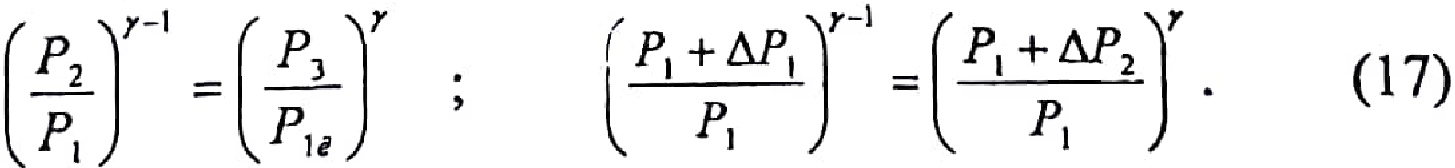

Логарифмирование формулы (17) лает результат

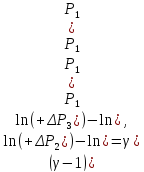
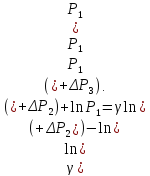
Решая это уравнение, получаем

(18)

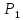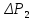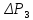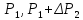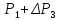Так как атмосферное давление много больше и и, соответственно, давления и мало отличаются друг от друга, то разности логарифмов можно принять пропорционально разности самих давлений. Исходя из этого предположения, получим расчетную формулу для определения отношения теплоёмкостей

(18)

Для записи результатов измерений подготовить таблицу.

№ опыта			γ	Δγ
1
2
3
4
5
Ср.

Число опытов и возможные значения ΔР задает преподаватель или лаборант. Для каждого замера определите у и его среднее значение по результатам всех опытов.

После проведения экспериментов вычислите 7 для воздуха, исходя из связи теплоемкостей газов и числа степеней свободы молекул и с учетом того, что воздух состоит преимущественно из двухатомных молекул (№ и 02). Сравните экспериментальное (среднее) и расчетное значение 7 для воздуха с учетом погрешностей.

Молярные теплоемкости можно найти на системы двух уравнений (11) и

(12).

	(20)
	(21)

РЕШЕНИЕ

№ опыта			γ	Δγ
1	214	60	1,39	0,01
2	216	62	1,4	0,02
3	216	58	1,37	-0,01
4	210	60	1,4	0,02
5	218	58	1,36	-0,02
Ср.			1,384	0,004

Так как воздух состоит из двухатомных молекул :
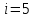