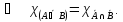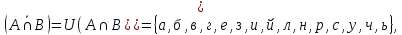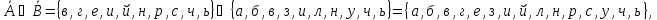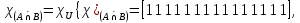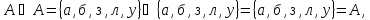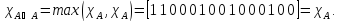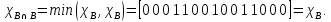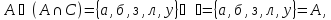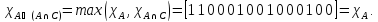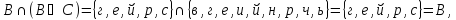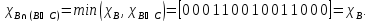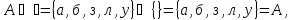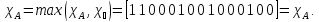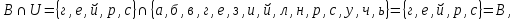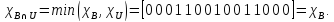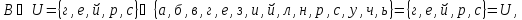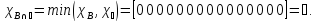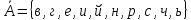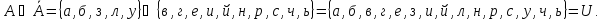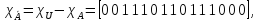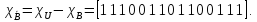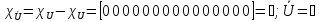ИДЗ №1 (И. И. Супрунов)
.docxРешение
-
Формирование множеств
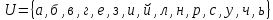 ,
,
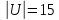 ;
;
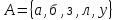 ,
,
 ;
;
 ,
,
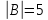 ;
;
 ,
,
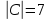 .
.
-
Отношение включения. Рассмотрим отношение включения множеств А, В, С и U между собой.
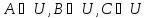 – по
условию задачи. Кроме того, так как
– по
условию задачи. Кроме того, так как
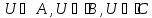 ,
то
множества А,
В,
С
являются строгими подмножествами
универсального множества U,
т.е.
,
то
множества А,
В,
С
являются строгими подмножествами
универсального множества U,
т.е.
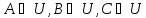 .
.
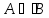 ,
так как существует элемент множества
А,
который не принадлежит множеству В,
например,
,
так как существует элемент множества
А,
который не принадлежит множеству В,
например,
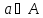 ,
но
,
но
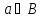 .
.
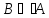 ,
так как существует элемент множества
В,
который не принадлежит множеству А,
например
,
так как существует элемент множества
В,
который не принадлежит множеству А,
например
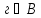 ,
но
,
но
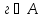 .
.
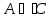 ,
так как существует элемент множества
А,
который не принадлежит множеству С,
например
,
так как существует элемент множества
А,
который не принадлежит множеству С,
например
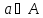 ,
но
,
но
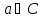 .
.
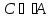 ,
так как существует элемент множества
С, который не принадлежит множеству А,
например
,
так как существует элемент множества
С, который не принадлежит множеству А,
например
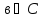 ,
но
,
но
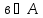 .
.
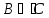 ,
так как существует элемент множества
В,
который не принадлежит множеству С,
например
,
так как существует элемент множества
В,
который не принадлежит множеству С,
например
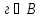 ,
но
,
но
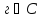 .
.
 ,
так как существует элемент множества
С,
который не принадлежит множеству В,
например
,
так как существует элемент множества
С,
который не принадлежит множеству В,
например
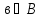 ,
но
,
но
 .
.
Отношение равенства
Так
как
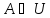 ,
но
,
но
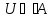 ,
то
,
то
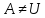 .
.
Так
как
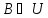 ,
но
,
но
 ,
то
,
то
 .
.
Так
как
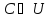 ,
но
,
но
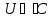 ,
то
,
то
 .
.
Так
как
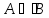 и
и
 ,
то
,
то
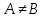 .
Так
как
.
Так
как
 и
и
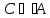 ,
то
,
то
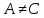 .
Так
как
.
Так
как
 и
и
 ,
то
,
то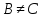 .
.
Отношение эквивалентности
Множества являются эквивалентными, если их мощности равны.
Так
как
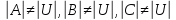 ,
то
,
то
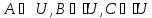 .
.
Так
как
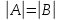 ,
то
,
то
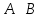 .
Так
как
.
Так
как
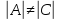 ,
то
,
то
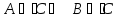
-
Характеристические функции
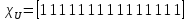 ,
,
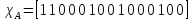 ,
,
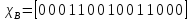 ,
,
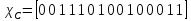 .
.
-
Проверка законов теории множеств
|
а) |
|
|
б) |
|
 .
.
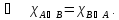
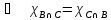 .
.
Законы коммутативности
Законы ассоциативности
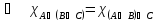
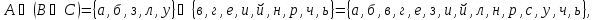
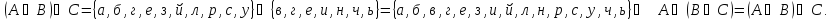

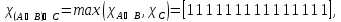


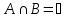
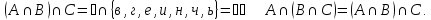
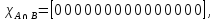
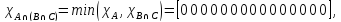
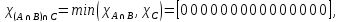
Законы дистрибутивности
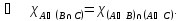

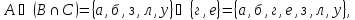
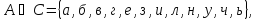
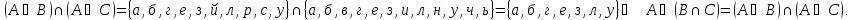
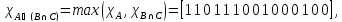
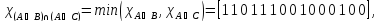
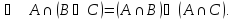

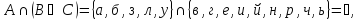
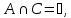
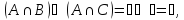
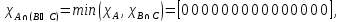
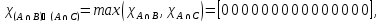
Законы де Моргана
|
а) |
|
|
б) |
|
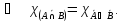
Законы идемпотентности
|
а) |
|
|
б) |
|
Законы поглощения
|
а) |
|
|
б) |
|
Законы тождества
|
а) |
|
|
б) |
|
Законы констант
|
а) |
|
|
б) |
|
Законы дополнения
|
а) |
|
|
б) |
|
|
в) |
|
|
г) |
|
Законы инволюции
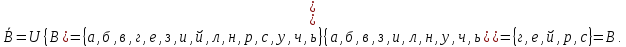
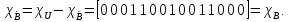
-
Формирование комплектов
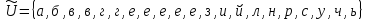 ,
,
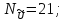
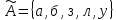 ,
,
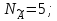
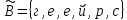 ,
,
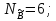
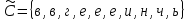 ,
,
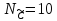 .
.
-
Функции экземплярности
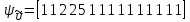 ,
,
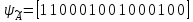 ,
,
 ,
,
 .
.
-
Проверка законов теории множеств
Закон дистрибутивности

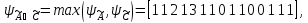

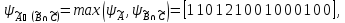
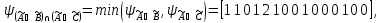
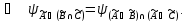
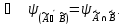
Закон
де Моргана
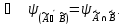

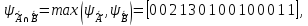
Закон поглощения
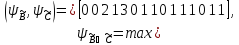


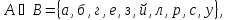
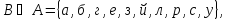
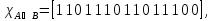
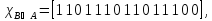
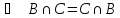
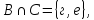
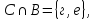
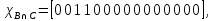
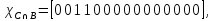
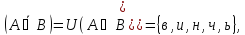
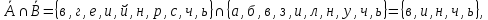
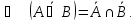
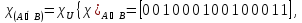
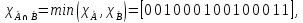
 .
.