Лабораторная работа №1 Многочлен Уилкинсона
Корнями
многочлена являются:
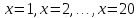
>> p=poly(1:20);
>> roots(p)
ans =
20.0003
18.9972
18.0112
16.9711
16.0483
14.9354
14.0653
12.9491
12.0334
10.9840
10.0061
8.9984
8.0003
7.0000
6.0000
5.0000
4.0000
3.0000
2.0000
1.0000
Видим, что корни полинома найдены приближенно.
Изменим значение, например, второго
уоэффициента полинома на малую величину
(составляющую
от числа):
>> p(2)=p(2)+10^(-7);
>> roots(p)
ans =
20.4220 + 0.9992i
20.4220 - 0.9992i
18.1573 + 2.4702i
18.1573 - 2.4702i
15.3150 + 2.6988i
15.3150 - 2.6988i
12.8466 + 2.0627i
12.8466 - 2.0627i
10.9213 + 1.1037i
10.9213 - 1.1037i
9.5678
9.1137
7.9941
7.0002
6.0000
5.0000
4.0000
3.0000
2.0000
1.0000
Видим, что половина корней стала комплексными. Из этого можно сделать вывод, что исходная задача неустойчива к входным данным.
Представление числа в компьютере
Число формата double –
64-разрядное число (8 байт), в котором 1
бит – знаковый, 52 отводятся под мантиссу
и 11 под порядок числа. (
,
- мантисса числа, n
- порядок). Так как в порядке тоже есть
знаковый бит, то множество его значений
лежит от
до
.
>> 2^1023
ans = 8.9885e+307
>> 2^1024
ans = Inf
>> realmax
ans = 1.7977e+308
>> realmin
ans = 2.2251e-308
Мантиса числа содержит 15-16 десятичных знаков, а все, что выходит за эти пределы, отбрасывается. Убедимся в этом:
>> format long e
>> sqrt(2)
ans = 1.414213562373095e+000
Если сложить
в мантиссу уложатся 15 десятичных знаков
и будет получен верный результат, а если
выполнить
,
то малое число выйдет за разрядную
сетку, и получим те же
>> 10^8+10^-7
ans = 1.000000000000001e+008
>> 10^8+10^-8
ans = 1.000000000000000e+008
Найдём значение выражения
при
,
где
Очевидно, что значением данного выражение
является единица при любых
.
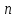step=0;
for n=0:55
step=step+1;
e=2^(-n);
answer=(1+e-1)/e;
fprintf('Шаг %d. epsilon=%d Результат=%d \n',step,e,answer);
end
Шаг 1. epsilon=1.000000e-000 Результат=1
Шаг 2. epsilon=5.000000e-001 Результат=1
Шаг 3. epsilon=2.500000e-001 Результат=1
Шаг 4. epsilon=1.250000e-001 Результат=1
Шаг 5. epsilon=6.250000e-002 Результат=1
...
Шаг 50. epsilon=1.776357e-015 Результат=1
Шаг 51. epsilon=8.881784e-016 Результат=1
Шаг 52. epsilon=4.440892e-016 Результат=1
Шаг 53. epsilon=2.220446e-016 Результат=1
Шаг 54. epsilon=1.110223e-016 Результат=0
Шаг 55. epsilon=5.551115e-017 Результат=0
Видим, что на 54-м шаге результ вычисления неожиданно стал равен нулю. Объяснить это можно тем, что на этом шаге складываются два числа, порядок которых сильно отличается, поэтому прибавяя к единице столь малое число, компьютер получает получает всё ту же единицу, а затем, вычитая из неё другую единицу, получает в числителе ноль.
Погрешности численных методов
Используюя следующий алгоритм вычисления
интеграла, наёдем с помощью MatLab
его значение для различных
.
и т.д.
Подынтегральная функция на всем отрезке
интегрирования неотрицательна,
следовательно, и значение интеграла –
положительное число. Более того,
подынтегральная функция на данном
интервале ограничена функцией
,
т.е. значение интеграла не может превышать
единицы.
Посмотрим на результаты MatLab:
I0=1/exp(1);
fprintf('I1=%f \n',I0);
for n=2:30
I=1-n*I0;
fprintf('I%d=%f \n',n,I);
I0=I;
end
I1=0.367879
I2=0.264241
I3=0.207277
I4=0.170893
I5=0.145533
...
I15=0.058961
I16=0.056621
I17=0.037447
I18=0.325949
I19=-5.193040
I20=104.860796
I21=-2201.076725
I22=48424.687947
I23=-1113766.822771
I24=26730404.746505
I25=-668260117.662624
I26=17374763060.228214
I27=-469118602625.161800
I28=13135320873505.531000
I29=-380924305331659.370000
I30=11427729159949784.000000
Видим, что на 19-ом шаге значение интеграла стало вдруг отрицательным, а дальше значение стали вообще абсурдными.
Объяснить это можно следующим образом: на самом деле значение интеграла было подсчитанно с некоторой погрешностью уже на первом шаге, а на следующих шагах погрешность возрастала и складывалась, т.е.
и так далее... Это приводит к возникновению существенно большой погрешности, в результате чего получается неверный результат.