Упражнение 3. Вычислить площадь треугольника с помощью векторного произведения

Вычислить площадь треугольника с вершинами иИзобразить плоскость треугольника. Как соотносятся (алгебраически и геометрически)площадь треугольника и векторное произведение. Изобразить это соответствие по аналогии с предыдущим упражнением.

Отметим, что векторное произведение векторов и смешанное произведение векторов (которого мы здесь не касались) наряду со скалярным произведением используется не только для вычисления площадей и объёмов, но является одним из основных инструментов для исследования прямых и плоскостей в пространстве (задач на составление уравнений прямых и плоскостей, взаимное расположение прямых и плоскостей и т.д.).

3. Прямая на плоскости.

   1. Уравнение прямой линии, проходящей через заданную точку перпендикулярно заданному вектору.

(нумерацию рисунков и формул начнем заново)

Пусть на плоскости (см. рис.1) заданы декартовая система координат OXY, точкаи ненулевой вектор, где числаA и B любые действительные числа, неравные нулю одновременно.

Требуется построить прямую L, проходящую через точку перпендикулярно направлению вектора, и составить ее уравнение

Рассмотрим вектор , где- любая точка прямойL. Точка M принадлежит прямой L тогда и только тогда, когда , см. рис.2.

Рис.1. Рис.2.

Значит, будет выполняться условие равенства нулю скалярного произведения между взаимно перпендикулярными (ортогональными) векторами

(1)

Уравнение (1) – векторное уравнение прямой L, проходящей через заданную точку перпендикулярно вектору .

Вектор называетсянормальным вектором прямой.

Иными словами нормальный вектор прямой - это ненулевой вектор, перпендикулярный прямой.

Записав векторное уравнение (1) в координатной форме получим: если прямая L имеет нормальный вектор и проходит через точку, то её уравнение может быть записано в виде:

. (2)

При построении прямой линии будем использовать функцию plot(x,y), в которой аргумент y будет вычисляться по формуле . Координаты нормального вектораи координаты точки прямойявляются входными параметрами в системуMATLAB.

2. Построение уравнения прямой, проходящей через заданную точку перпендикулярно данному вектору.

Задача. Построить в тетради и в MATLAB прямую L, проходящую через точку с нормальным вектором. Записать и вывести в заголовок уравнение прямой вида (2).

Обучающий пример будет состоять из трех частей. Мы постепенно освоим процедуру создания графической иллюстрации к задачам аналитической геометрии. При написании программ, главным образом, нужно стремиться к тому, чтобы команды тела программы были написаны в общем виде (как это будет показано в части 3), а в комментариях описываем эти команды с конкретными числовыми данными и с ожидаемым результатом на основе письменного решения.

Часть 1.

Построить штриховую «--» прямую линию красного цвета толщины 2.

Значение абсцисс точек прямой изменяются в диапазоне от – 2 до 6 с шагом 2.

В узловых точках вывести маркеры красного цвета «r» в виде шестиконечных звезд «h».

Вопрос: сколько будет узловых точек у функции plot( )?

В заголовок вывести общее уравнение прямой.

Построить и обозначить оси координат.

Отметить точку .

Решение:

В окне редактора Editor создаем М-файл (скрипт):

% часть 1

% задание исходных данных - коэффициентов уравнения и начальной точки M0(4,2):

A=-1; B=1; x0=4; y0=2;

% формирование диапазона абсцисс

x=-2:2:6; % массив размерности 1х5;

% Вычисление значений ординат

y=(-A/B)*(x-x0)+y0; % также получим массив размерности 1х5;

% Вопрос: сколько будет узловых точек у функции plot( )?

% Ответ:

% Так как для аргументов функции plot были созданы массивы размерности1х5,

% то узловых точек будет 5.

% построение красной штриховой линии с 5-ю маркерами в виде 6-конечных звезд

plot(x,y,'r--h', 'LineWidth',2)

% построение осей координат

line([-3,0;7,0],[0,-5;0,5],'Color','black')

% обозначение осей и ввод заголовка

xlabel('X'),ylabel('Y'), title(' -3 (x - 4) + 3 (y - 2) = 0')

% включим отображение координатной сетки и режим добавления графиков

grid on, hold on

% установим одинаковый масштаб

axis equal

% обозначим прямую L и точку M0(4,2)

% пометим прямую L

text(-1.75,-2.5,'L')

%пометим точку M0(4,2) круговым маркером черного цвета

plot(4,2,'o','LineWidth',2,...

'MarkerEdgeColor','k',...

'MarkerSize',8)

% и выведем обозначение точки M0(4,2)

text(4.2,1,'M_0(4,2)')

Получаем график (рис.3) прямой L: , проходящей через точку.

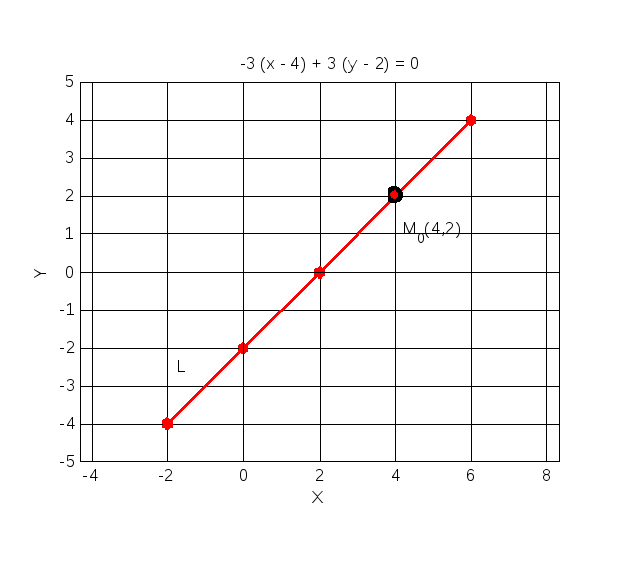
Рис.3.