Способ 4. Построение графика cпомощьюpolar.
Для отображения
графиков функции в полярных координатах
удобно использовать команду «polar».
Так, например, можно реализоватьполярную
розу
.
n=3;a=1;phi=0:pi/180:2*pi;
polar(phi, a*sin(n*phi),'r');
При обращении к полярным координатам в средах MATLAB или Wolfram Mathematica, следует отметить, что в этих средах допускается отрицательность радиуса в полярной системе координат, что нарушает взаимно однозначность при сопоставлении декартовой и полярной систем координат.
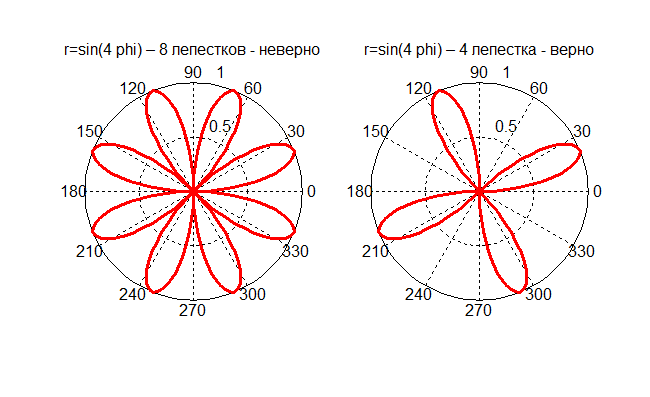
Например, если мы ничего не предпримем, то в случае с четным n,например,n= 4, мы получим 8 лепестков (а должно быть четыре).
Отрицательные
значения радиуса «отражаются» в
противоположном направлении полярной
оси
относительно полюсаO.
Для того чтобы ограничить r, можно ввести, например, «r=max(0,r)».
n=4; a=1; phi=0:pi/100:2*pi;
r=a*sin(n*phi);
subplot(1,2,1)
polar(phi, r,'r')
title('r=sin(4 phi) – 8 лепестков - неверно')
subplot(1,2,2)
r=max(0,r);
polar(phi, r,'r')
title('r=sin(4 phi) – 4 лепестка - верно')
Но лучше написать свою программу по отбору нужных значений радиусов.
Упражнение 4. Построение полярной розы.
Напишите подобную
программу, для
.
Используйте циклы for end; if end.
n=4; a=1;
for phi=0:pi/100:2*pi;
r=a*sin(n*phi);
if (r>=0) действие end
polar(phi, r,'r');
end
Упражнение 5. Уравнения однолепестковых роз в полярной системе координат, построение.
Построить графики
в полярных координатах с помощью функции
«polar»
.
Сравните полученные результаты с
результатами упражнения 2.
Упражнение 6. Линии в декартовых и полярных координатах.
Построить линии
,x=1,y=1 в
декартовой системе координат с помощью
различных команд. Перейти к полярной
системе координат, построить линии в
полярных координатах с помощью функции
«polar». Сравнить,
прокомментировать полученные результаты.
Преобразование системы координат
Поворот системы координат
Пусть заданы
прямоугольная декартовая система координат OXY;
точка M с декартовыми координатами (x,y).
Можно также сказать,
что положение точки на плоскости
определяются
- радиус-вектором
точкиM.
(φ, r) - полярные координаты точкиM
Рассмотрим два случая и найдем связь между ними. В первой мы будем рассматривать поворот координатных осей относительно начала координат на угол α (альфа) в положительном направлении. Во второй - поворот радиус-вектора точки Mна угол α (альфа) в положительном направлении относительно начала координат.
Случай 1. Поворот координатных осей относительно начала координат
Назовем OXY- старой системой координат,OX 'Y '
- новой. На рисунке точкаMосталась неподвижной. Теперь у нее есть
старые (x,y)
и новые (x ',y ')
координаты. Составим формулы перехода
между старыми и новыми координатами
через полярную систему координат.
Напомним
- полярный
радиус.
Согласно рисунку слева
,
(1)
,
(2)
,
получили формулы перехода от старых координат к новым при повороте координатных осей на угол α (при α >0 против часовой стрелке):
.
(3)
Теперь обратно.
Согласно рисунку
справа:
, (4)
тогда
, (5)
,
,
получили формулы перехода от новых координат к старым:
.
(6)
При этом в старой системы координат OXY
базисом являются
орты
,
базисом новой
системы координат - орты
,
Связь между ортами, согласно (3) и (6)
(7),
(8).
Что это значит?
Например, точка Mимеет
старой системе координаты
То есть радиус-вектор
точки можно записать
.
Найдем теперь, чему равны координаты этой же точки в новой системе координат, при повороте ее относительно старой на 45°. В силу (8) имеем:
-
координаты точки в старой и новой
системах координат. В новой системе
координат координаты точки выглядят
«приятней». Целью преобразования системы
координат является поиск наиболее
«удобной» для изучения объекта системы
координат.