Контрольное мероприятие № 4. Защита л.2.1, л.2.2, л.2.3

проводится на 16-ой неделе.

Темы индивидуальных заданий Линейная алгебра.

Продумать решения каждой задачи средствами MATLAB. Продумать иллюстрации в MATLAB.

Задания, выдаваемые студенту, могут незначительно отличаться от нижеследующих.

1. Вычислить ранг матрицы методом элементарных преобразований строк. Проверить соответствующей встроенной функцией МАТЛАБ.

2. Найти обратную матрицу A^-1 методом элементарных преобразований в МАТЛАБ, если . Сделать проверку. A*A^-1 = E

3. Решить методом Гаусса и LU- разложением.

Найти число обусловленности и оценить - относительную погрешность решения систем, подобрав какой-нибудь вектор db ≠ 0 – погрешность (возмущение ) правой части. Решить системы методом простой итерации. . Проверить выполнение условий для матрицы .

4. Решить матричное уравнение методом элементарных преобразований.

5. Найти число обусловленности и оценить - относительную погрешность решения систем, подобрав какой-нибудь вектор db ≠ 0 – погрешность (возмущение ) правой части.

6. Найти собственные векторы и собственные значения линейного оператора, заданного матрицей и проверить результат с помощью функции eig()

>> d=eig(A) %Функция вычисляет собственные значения матрицы A.

>>[U,D]=eig(A) %Матрица V состоит правых собственных векторов, удовлетворяющих соотношению A * V= V * D. Эти векторы нормированы так, что норма каждого из них равна единице.

7. Привести матрицу линейного оператора к диагональному виду и найти соответствующий базис. Результаты поверить с помощью функции eig ()

8. Для матрицы найти диагональную матрицу D и унитарную (ортогональную) матрицу U и проверить результат с помощью функции eig()

9. Найти собственные числа и собственные векторы линейного оператора, заданного матрицей .

Сначала найти на листочке, затем с помощью встроенных команд МАТЛАБ проверить себя.

10. В пространстве L³ заданы векторы в некотором базисе. Доказать, что векторы составляют базис, найти матрицу перехода в базисе , найти координаты вектора в базисе . .

11. Заданы векторы 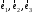в некотором базисе. Проверить, что векторы составляют базис. Применяя процесс ортогонализации Шмидта построить новый ортогональный базис. .

Задачу сначала решить на листочке. Опорные вычисления проверяйте на МАТЛАБ. Затем сделать графическую трехмерную иллюстрацию в МАТЛАБ. Изобразите заданные векторы, векторы нового базиса, орты нового базиса, вспомогательные векторы (демонстрирующие процесс ортогонализации). В графическом окне выведите списком, за какие цветные линии - векторы отвечают за те или иные векторы из задачи.

12. Определить, является ли положительно определённой квадратичная форма

.

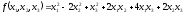13 . Методом Лагранжа привести форму к каноническому виду:

14. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду

15. Записать каноническое уравнение кривой второго порядка, определить тип и найти каноническую систему координат. Применить теорию квадратичных форм.

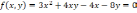
16. Записать каноническое уравнение поверхности второго порядка, определить тип и найти каноническую систему координат. Применить теорию квадратичных форм.

17. Определить по критерию Сильвестра какие квадратичные формы являются квадратичными или отрицательными, а какие нет.

1) ; 2) ; 3) ;

4) ;

5) ;

6) ; 7).

1. Список рекомендуемой литературы

1. А. Кривелёв. Основы компьютерной математики с использованием системы MATLAB. М, 2005.

2. В.А.Ильин, Э.Г.Позняк. Аналитическая геометрия. М.,Наука,2001, Шифр – 514.12(075.8) И-46.

3. Ржавинская Е.В., Соколова Т.В., Олейник Т.А. Лекции по линейной алгебре и аналитической геометрии, М.,МИЭТ. 2007.

4. Сборник задач по математике для втузов под редакцией А.В.Ефимова, А.С.Поспелова. В 4 частях. Часть 1.(4-е изд. перераб. и доп.)2001, 2004.