
- •Порядок выполнения.
- •Геометрические векторы и линейные операции над ними.
- •Свойства операции сложения геометрических векторов:
- •Построение векторов в графическом окне matlab.
- •Построение прямых. Команда line.
- •Размещение нескольких рисунков в одном графическом окне.
- •Пример 1. Разбиение графического окна на несколько областей.
- •Построение векторов на плоскости.
- •Пример 2. Векторы на плоскости
- •Построение векторов в пространстве.
- •Скрипты, м – файлы.
- •Создание Script m–Files
- •Упражнение 6. Для самостоятельной работы.
- •Упражнение 7. Для самостоятельной работы.
- •Упражнение 8. Правило треугольника.
- •Упражнение 9. Правило параллелограмма.
- •Упражнение 10. Сумма и разность векторов.
- •Логическое равенство.
- •Упражнение 11. Свойства суммы векторов
- •Упражнение 12. Проверить свойства умножения вектора на число.
- •Длина вектора
- •Упражнение 13. Длина вектора, орт вектора. Пространство.
- •Упражнение 14. Длина вектора, орт вектора. Плоскость.
- •Направляющие косинусы
- •Определение
- •Упражнение 18. Изобразить векторы базиса. Пространство.
- •Упражнение 19. Изобразить векторы базиса. Плоскость.
- •Упражнение 20. Разложение вектора по двум неколлинеарным векторам.
- •Упражнение 21. Разложение вектора по трем некомпланарным векторам.
- •Упражнение 22. Линейная зависимость четырёх векторов.
- •Косоугольная и прямоугольная система координат.
- •Скалярное произведение векторов
- •Пример 2.Вычисление скалярного произведения в косоугольном базисе, состоящем из единичных векторов.
- •Пример 3.Вычисление скалярного произведения в косоугольном базисе, состоящем из векторов произвольной длины.
- •Скалярное произведение в координатной форме
- •Упражнение 26. Скалярное произведение в координатной форме.
- •Контрольные вопросы
- •Контрольное мероприятие № 1. Защита л.1.1 и л.1.2.
- •Индивидуальные задания № 1 Векторная алгебра.
- •Список рекомендуемой литературы
Индивидуальные задания № 1 Векторная алгебра.
Задания разного уровня сложности.
Задачи необходимо иллюстрировать в MATLAB
1.
Дан правильный шестиугольник
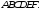 Точка
Точка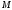 – середина стороны
– середина стороны Выразить вектор
Выразить вектор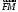 через векторы
через векторы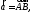


.
2.
В параллелограмме

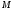 и
и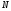 – середины сторон
– середины сторон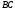 и
и соответственно. Выразить вектор
соответственно. Выразить вектор через векторы
через векторы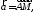
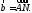

3.
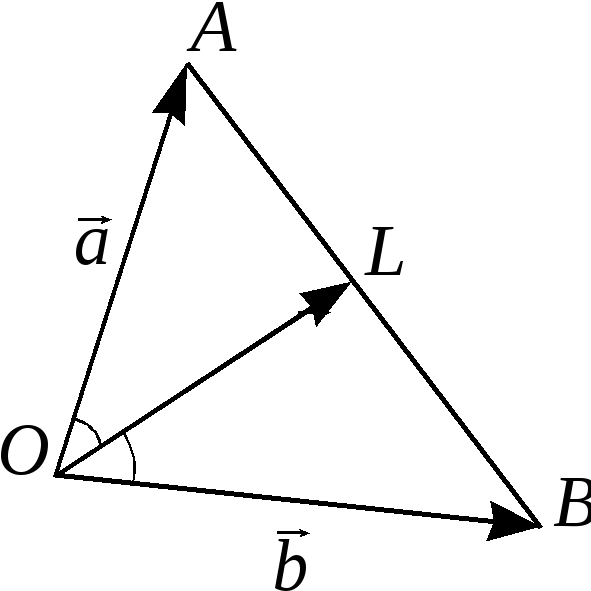
В треугольнике
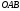
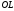 – биссектриса угла
– биссектриса угла Выразить вектор
Выразить вектор через векторы
через векторы
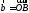 и длины этих векторов.
и длины этих векторов.
4.
Пусть
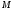 – точка пересечения медиан треугольника
– точка пересечения медиан треугольника Вычислить сумму
Вычислить сумму

5.
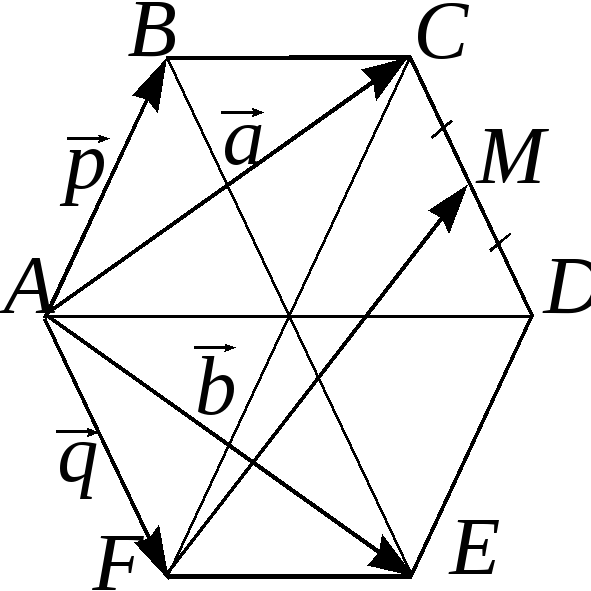
Дан правильный шестиугольник
 Точка
Точка – середина стороны
– середина стороны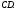 Разложить вектор
Разложить вектор по базису
по базису

6.
На сторонах
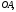
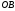 треугольника
треугольника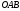 соответственно взяты точки
соответственно взяты точки и
и такие, что
такие, что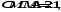
 Пусть
Пусть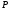 – точка пересечения отрезков
– точка пересечения отрезков и
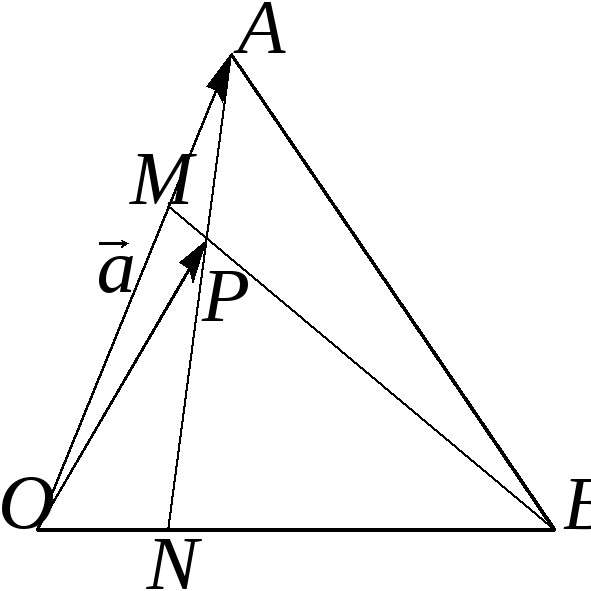
и Разложить вектор
Разложить вектор по базису
по базису
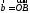
7. Доказать, что высоты треугольника пересекаются в одной точке.
Указание.
Пусть
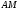 и
и – высоты, пересекающиеся в точке
– высоты, пересекающиеся в точке Утверждение будет доказано, если мы
покажем, что
Утверждение будет доказано, если мы
покажем, что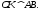 Переформулируем нашу задачу на языке
скалярного произведения:
Переформулируем нашу задачу на языке
скалярного произведения:
дано:

доказать:
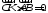
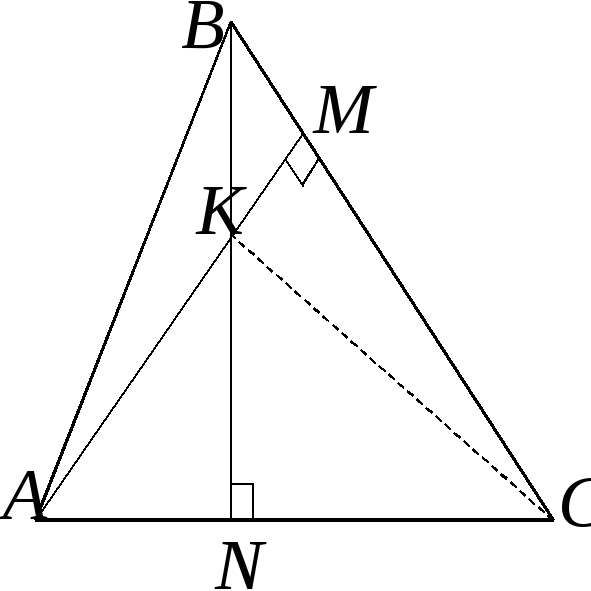
8.
В треугольнике
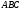 проведена высота
проведена высота Выразить вектор
Выразить вектор через векторы
через векторы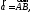


9.
Пусть

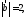
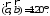
Вычислить:
1)
 2)
2)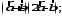 3)
3)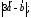 4)
4) 5)
5)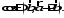
Следующие две задачи наглядно показывают возможности скалярного произведения для решения задач элементарной геометрии. Например, для нахождения длин отрезков и для вычисления углов между скрещивающимися прямыми.
10. Все рёбра правильной треугольной призмы равны 1. Найти угол между скрещивающимися диагоналями двух боковых граней призмы.
Решение (см. рис. 17).
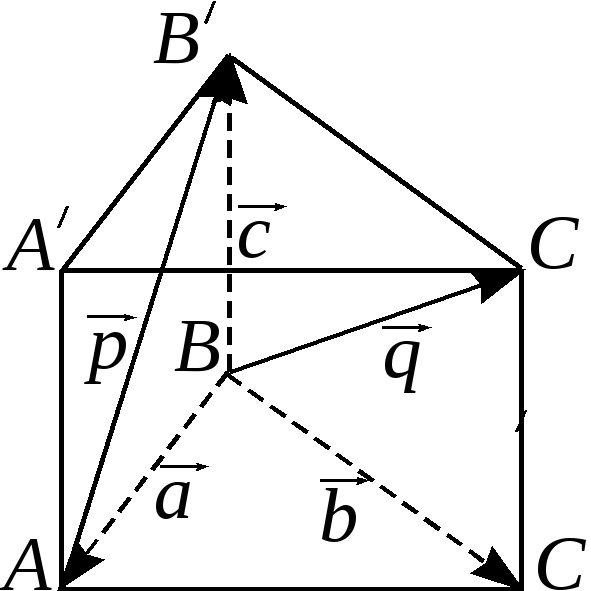
11.
Все грани параллелепипеда – ромбы со
стороной 1 и углом
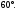 Найти наибольшую диагональ параллелепипеда.
Найти наибольшую диагональ параллелепипеда.
Дан правильный шестиугольник
 Точка
Точка – середина стороны
– середина стороны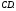 Выразить вектор
Выразить вектор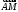 через векторы
через векторы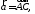
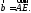
Точка
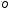 – центр правильного шестиугольника
– центр правильного шестиугольника Выразить вектор
Выразить вектор через векторы
через векторы
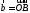
В треугольнике


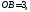
 Из точки
Из точки опущена высота
опущена высота Разложить вектор
Разложить вектор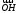 по базису
по базису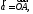

В треугольнике
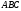 проведены медианы
проведены медианы
 и
и пересекающиеся в точке
пересекающиеся в точке Разложить вектор
Разложить вектор по базису
по базису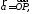
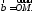
В параллелограмме
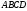 точка
точка – середина стороны
– середина стороны Разложить вектор
Разложить вектор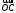 по базису
по базису

Доказать, что в любой трапеции следующие 4 точки лежат на одной прямой: середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон.
Пусть
 – точка пересечения медиан треугольника
– точка пересечения медиан треугольника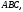 а
а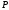 – произвольная точка. Доказать, что
– произвольная точка. Доказать, что
Пусть
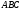 и
и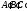 – треугольники,
– треугольники, и
и – точки пересечения медиан этих
треугольников соответственно. Выразить
вектор
– точки пересечения медиан этих
треугольников соответственно. Выразить
вектор через векторы
через векторы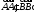 и
и
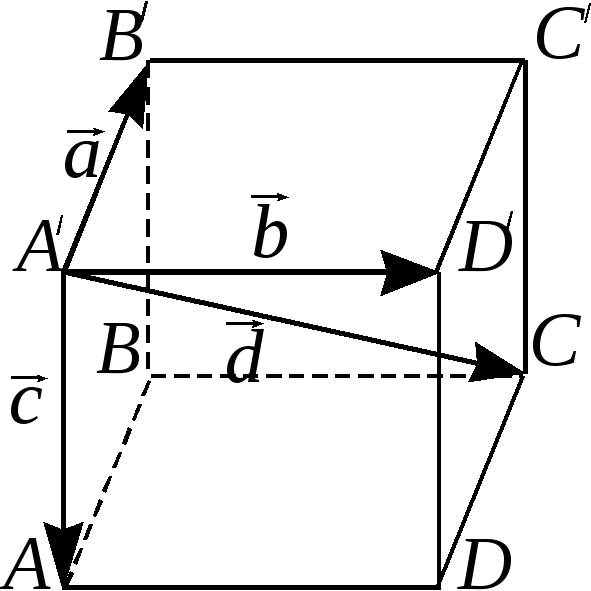
Дан параллелепипед
 Разложить вектор
Разложить вектор по базису
по базису

Список рекомендуемой литературы
А. Кривелёв. Основы компьютерной математики с использованием системы MatLab. М, 2005.
В.А.Ильин, Э.Г.Позняк. Аналитическая геометрия. М.,Наука,2001, Шифр - 514.12(075.8) И-46.
Ржавинская Е.В., Соколова Т.В., Олейник Т.А. Лекции по линейной алгебре и аналитической геометрии, М.,МИЭТ. 2007.
Сборник задач по математике для втузов под редакцией А.В.Ефимова, А.С.Поспелова. В 4 частях. Часть 1.(4-е изд. перераб. и доп.)2001, 2004.
