6. Уравнения плоскости в пространстве.

   1. Различные уравнения плоскости.

(Начнем заново нумерацию всех формул и рисунков.)

Поверхность в пространстве рассматривается как геометрическое место точек, удовлетворяющих какому-либо условию. Уравнением поверхности в прямоугольной системе координат называется такое уравнение , которому удовлетворяют координаты каждой точки, принадлежащей поверхности, и не удовлетворяют координаты точек, не принадлежащих этой поверхности. Простейшей поверхностью является плоскость.

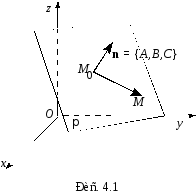
Рис.1.

Нормальным вектором плоскости называется любой ненулевой вектор, перпендикулярный этой плоскости. Пусть – нормальный вектор плоскости π и- фиксированная точка плоскости π (см. рис. 1).

Точка пространства принадлежит плоскости π тогда и только тогда, когдаа значит, имеет место равенство

(1)

выражающее векторное уравнение плоскости. Из уравнения (1) ввиду того, что мы получаем уравнение плоскости в виде

(2)

или общее уравнение плоскости:

(3)

где .

Для того чтобы составить уравнение плоскости, из условия той или иной задачи находят нормальный вектор и точку, принадлежащую точке. После этого записывают уравнение в виде (2). Раскрывая скобки и приводя подобные члены, получают уравнение в виде (3).

Если известны длины отрезков, отсекаемых плоскостью от осей координат, то имеет место уравнение плоскости “в отрезках”:

(4)

2. Построение плоскости графическим средствами matlab.

В МАТЛАБ плоскость (поверхность) можно изображать с помощью различных функций: plot3(), mesh(),surf(), surfl(), surface(). Общим для всех этих функций является необходимость использовать функцию meshgrid. Посмотрите в help как они устроены. А также читайте Кривиёва стр. 153.

Функция plot3() позволяет строить графики по точкам и выводить маркеры точек в координатном пространстве.

Для того чтобы проще было понять роль функции meshgrid рассмотрим простой пример с выводом массивов на экран. В этом же примере мы познакомимся также с функцией view(). Прочтите в help и/или в Кривилёве на стр.151 как она работает.

Пример. 1. Общее уравнение плоскости. Функция meshgrid.

Построить плоскость, заданную общим уравнением 3 x+ 4y+ 6z– 12 = 0.

Решение:Создадим скрипт, в ходе создания разберем работу функции meshgrid.

% оформление графика

xlabel('x'), ylabel('y'), zlabel('z')

title('3 x + 4 y +6 z - 12 = 0')

hold on, axis equal, grid on

% зададим оси координат

line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',1.5, 'Color', 'black' )

% вводим исходные данные

% но код преимущественно будем писать в общем виде

A = 3; B = 4; C = 6; D = -12;

% задаем диапазоны изменения переменных x и y в виде массивов, строк-векторов.

x=0:1:4; % массив 1х5, вектор из 5-ти элементов

y=0:1:3, % массив 1х4, вектор из 4-ех элементов

% С помощью функции meshgrid начальные векторы x и y

% трансформируются в матрицы X и Y.

% При этом число столбцов в матрицах соответствует

% числу элементов в векторе x,

% а число строк в матрицах соответствует

% числу элементов в векторе y.

% на входе принимает значения векторов x и y, а на выходе дает матрицы X и Y

[X,Y]=meshgrid(x,y)

% Из уравнения плоскости выражаем Z.

Z = (-A*X-B*Y-D)/C

% plot3 выведет круговые маркеры черного цвета в узлах сетки, всего узлов 5х4=20.

plot3(X,Y,Z,'ok','MarkerSize',8, 'LineWidth',2)

При написании кода мы не подавляли вывод команд. Посмотрим, что выводится в командном окне.

Массив абсцисс xсостоит из пяти точек

x = 0 1 2 3 4

Массив ординат yсостоит из четырех точек

y = 0 1 2 3

Двумерный массив абсцисс Х 5х4 для каждой узловой точки сетки

X =

0 1 2 3 4

0 1 2 3 4

0 1 2 3 4

0 1 2 3 4

Двумерный массив ординат У 5х4 для каждой узловой точки сетки

Y =

0 0 0 0 0

1 1 1 1 1

2 2 2 2 2

3 3 3 3 3

Двумерный массив Z 5х4 для значений функции Z=f(X,Y) в каждой узловой точки сетки .Z=f(X,Y) понимается как функция двух переменных, задающая в общем случае поверхность, в нашем случае плоскость.

Z =

2.0000 1.5000 1.0000 0.5000 0

1.3333 0.8333 0.3333 -0.1667 -0.6667

0.6667 0.1667 -0.3333 -0.8333 -1.3333

0 -0.5000 -1.0000 -1.5000 -2.0000

Функция plot3 выводит круговые маркеры со значением аппликаты Zв узловых точках сетки (в точках области задания поверхности) с координатами (X,Y).

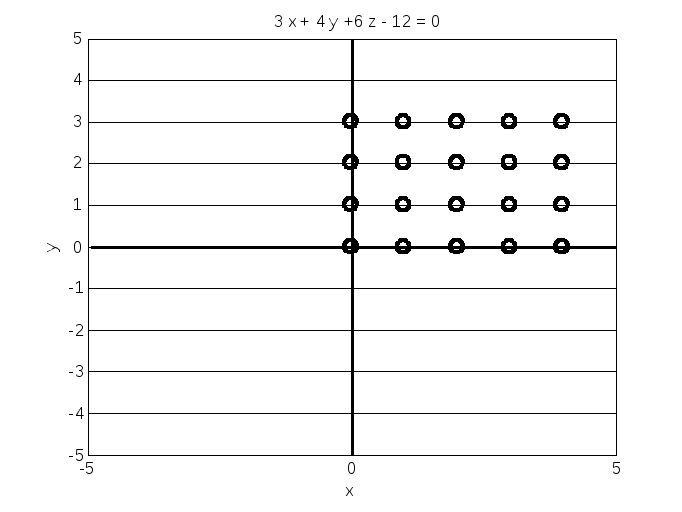
Рис. 2.

На рис.2 мы видим изображение 20-ти круговых маркеров.

Развернем график в пространстве с помощью Rotate; на рис.3 увидим распределение круговых маркеров по плоскости.

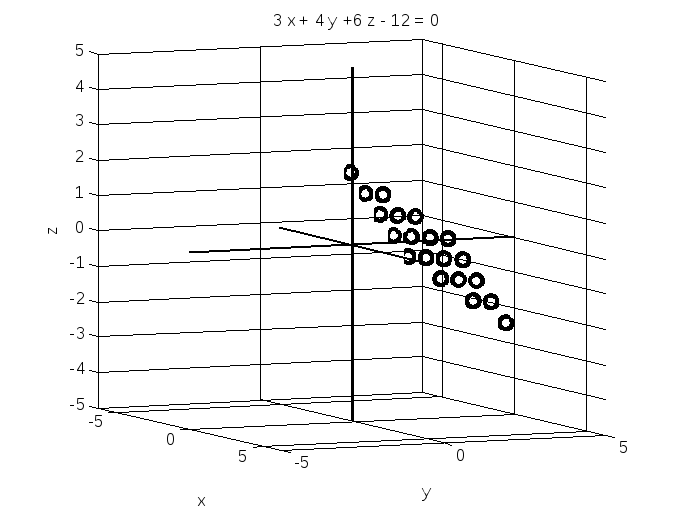
Рис. 3.

Добавим команду:

surf(X,Y,Z)

Функция surf () закрашивает каждую клетку плоскости (поверхности) определенным цветом, который зависит от значений массива аппликат Z. При этом из четырех узловых точек, ограничивающих клетку, выбирается и учитывается минимальная по значению. Изменение цвета на плоскости (поверхности) означает изменение по оси аппликат (высоте, глубине).

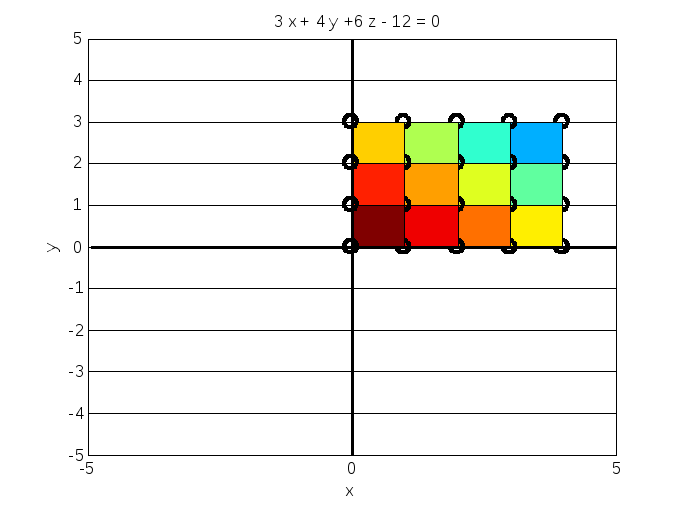
Рис. 4.

При вращении графика с помощью Rotate, в левом нижнем углу графического окна вы увидите, как меняются параметры Az и El. Выбрав наилучшее положение, например, Az:126 и El:22, мы можем написать соответствующую команду в скрипт, и после запуска программы картинка сама появиться в нужном ракурсе.

view(126,22)

Рис. 5.