Упражнение 8. Общее уравнение прямой.
Используя функцию
plot(), построить ту же
прямую, заданную общим уравнением
сплошную, зеленого цвета, толщины 2.
Значение абсцисс точек прямой – массив,
состоящий из двух точек -6 и 6.
В заголовок вывести общее уравнение прямой.
Построить и пометить оси координат.
Вывести квадратные маркеры в узловых точках линии.
Отобразить координатные оси черным цветом, пометить начало координат
Изобразить вектор
,
орт вектора
,
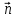берущими начало
а) из начала координат;
б) из точки (0,-2), лежащей на заданной прямой.
Программу снабдить комментариями.
Сделать выводы.
M -function
Рассмотренные в первом разделе пример и упражнения требовали от нас снова и снова строить прямые на плоскости. В следующем разделе нам также предстоит выполнять несколько раз одни и те же действия. Поэтому было бы полезно написать одну программу и пользоваться ей по мере необходимости. Ранее мы писали файл-программы с последовательностью команд MATLABвскриптах, в окне редактореEditor(M - File Script). В дальнейшем полезно и необходимо уметь составлять собственные файл-функции, которые производят необходимые действия с входными аргументами.
Создание м-файла.
Предположим, что нам надо построить несколько однотипных прямых линий. Имеет смысл один раз написать файл-функцию, а потом вызывать столько раз сколько потребуется. Откройте в редакторе M-Fileновое окно, наберите текст:
functionmyline(A,B,C,x)
y=-(A*x+C)/B;
plot(x,y,'r-', 'LineWidth',2)
grid on, hold on
axis equal
line([-8,0;8.5,0],[0,5;0,-9],'Color','black')
plot(8,0,'>k')
plot(0,5,'^k')
text(8,-0.5,'x')
text(-0.5,5,'y')
plot(0,0,'ok')
text(-0.5,-0.5,'O')
Слово «function» в первой строке определяет, что данный файл содержит файл-функцию. Первая строка являетсязаголовком функции, в которой размещаетсяимя функцииисписки входных аргументов. В примере 2 myline- имя функции, y – возвращаемое значение,A,B,C,x - четыре входных аргумента. После заголовка следуеттело функции,которое в данном примере состоит из 11-ти строк.
Теперь сохраните файл в рабочем каталоге. Выбор пункту SaveилиSaveasменю приводит к появлению диалогового окна сохранения файла, в полеFilenameкоторого уже содержится названиеmyline.Не изменяйте его, сохраните файл-функцию в файле с предложенным именемmyline.m.
Теперь созданную функцию можно использовать так же, как и встроенные стандартные функции MATLAB, например, из командной строки нужно набрать две строчки.
В первой строке мы вводим значения входных аргументов - трех коэффициентов общего уравнения прямой и матрицы для аргумента значений абсцисс x.
Вторая строка вызывает функцию myline, которая построит прямую.
>> A=1;B=-1;C=0;x=[-6,6];
>> myline(A,B,C,x)
Рис. 14
Построим еще одну прямую, с другими коэффициентами, но теперь значения аргументов мы разместим сразу внутри М-функции
>>myline(1,-1,-2,[-5,5])
Рис. 15
Первые четыре строчки функции можно посвятить описанию работы данной м-функции, а затем с помощью helpmylineвызвать это описание. Например, введите текст в тело М-функции:
functionmyline(A,B,C,x)
% Функция строит прямую по общему уравнению прямой.
% Для построения введите коэффициенты общего уравнения прямой A, B, C,
% а также диапазон изменения аргумента абсциссы x в виде массива 1х2
% Возвращаемое значение – ординаты прямой в точках x.
y=-(A*x+C)/B;
plot(x,y,'r-','LineWidth',2)
grid on, holdon
axis equal
line([-8,0;8.5,0],[0,5;0,-9],'Color','black')
plot(8,0,'>k')
plot(0,5,'^k')
text(8,-0.5,'x')
text(-0.5,5,'y')
plot(0,0,'ok')
text(-0.5,-0.5,'O')
Хороший стиль. Функции и скрипты.
Главное отличие скриптов от функций состоит в том, что скрипты исполняются в базовом рабочем пространстве (Base workspase), к которому пользователь имеет доступ из командной строки. Функции же исполняются в собственном пространстве переменных. Если в вашем базовом пространстве есть переменная X, то использовать её в функции нельзя, она её “не видит” и, как следствие, не может изменить. Эта особенность функций очень удобна – можно не бояться, что вызов функции как-то повлияет на ваши переменные. Функция может только вернуть значение.
Однако переменные – это ещё не всё, что можно ненароком испортить. Представьте, что в функцию myline мы включили команды по изображению координатных осей. Теперь мы не сможем использовать эту функцию, если оси нам рисовать не нужно, или мы хотим нарисовать их по-другому. Такие взаимодействия с «миром за пределом функции» называются побочными эффектами. К ним относится так же неподавленный вывод, функция disp(), команды hold и grid.
Отсюда правило написания функций: функция должна иметь минимально возможное количество побочных эффектов.
А рисование осей лучше вынести в скрипт.
Сохраните и вызовите описание функции из командной строки
>> help myline
Мы увидим:
Функция строит прямую по общему уравнению прямой.
Для построения введите коэффициенты общего уравнения прямой A, B, C,
а также диапазон изменения аргумента абсциссы x в виде массива 1х2
Вводим в командной строке:
>> A=1;B=-1;C=2;x=[-6,6];
>> myline(A,B,C,x)
Рис. 16