Упражнение 5. Уравнение прямой, проходящей через две точки.

Графическое окно разбить на две области. В первой области изобразить прямую L1, во второй – прямуюL2. В заголовки вывести соответствующие уравнения вида (4).

1. Прямая L1 задана двумя точкам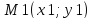ии.

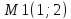
Определиться с входными данными.

Выразить из канонического уравнения y, как функцию отx.

Используя функцию plot(), построить прямуюL1. Пометить прямуюL1.

Отметить и подписать на прямой точки и.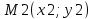

Провести с помощью функции line( ) оси координат черного цвета.

Пометить начало координат.

Найти и построить направляющий вектор 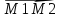, берущим начало

а) из начала координат, б) из точки .

Найти и построить нормальный вектор , берущим начало

а) из начала координат, б) из точки .

2. Сделать все тоже самое для прямой L2, проходящей через точкии.

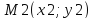
5. Параметрическое задание прямой.

Рассмотрим совсем иной подход к заданию прямой на плоскости, см. рис.9. Пусть на плоскости задана прямая, проходящая через точку в направлении вектора.

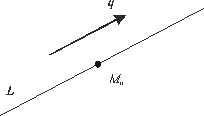
Рис. 9

Рассмотрим вектор , где- любая точка прямойL. Введем параметр t – любое вещественное число, см. рис.10.

Условие коллинеарности прямой и направляющего вектора с помощью параметра t можно записать в виде векторного уравнения: .

Отсюда понятен геометрический смысл параметра прямой t:

• модуль числа означает, сколько векторов“укладывается” на векторе,

• знак обозначает расположение точки на прямойL относительно :

при точканаходится с той стороны, куда направлен векторпри– в противоположной стороне, см. рис. 10.

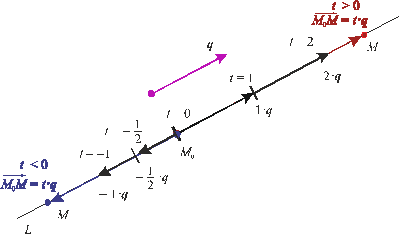
Рис. 10

Параметрическое уравнение прямой в векторной форме однозначно определяет прямую Lна плоскости и не зависит от системы координат.

Введем декартовую прямоугольную систему координат OXY, координаты точки, координаты направляющего вектораи координаты произвольной точки прямой.

Как было сказано выше, условие коллинеарности направляющего вектора и прямой - условие пропорциональности соответствующих координат векторов и . Вместе с параметромtполучаем соотношение:

(5)

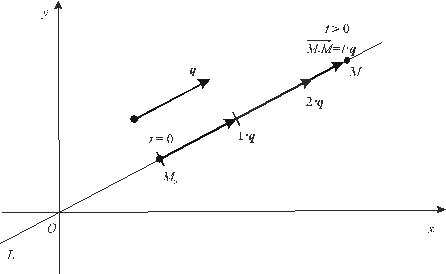
Рис. 11

Из уравнения (5) получаем два соотношения:

(6)

Уравнение (6) называется параметрическим уравнением прямой L, проходящей через точку параллельно направлению вектора.

Упражнение 6. Параметрическое задание прямой.

Построить прямую L, заданную параметрическим уравнением

.

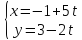Найти ее направляющий вектор 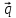и его орт, найти нормальный вектори его орт. Изобразить и пометить данные векторы исходящими из начала координат и из точки, соответствующей нулевому значению параметра t = 0. Пометить прямуюL.

6. Уравнение прямой с угловым коэффициентом

(7)

Рис.12.

Здесь – угловой коэффициент, т.е., где- угол наклона прямойк осиУравнением (7) может быть задана любая прямая, неколлинеарная оси

7. Уравнение прямойв отрезках.

(8)

Рис.13.

Здесь aиb– величины отрезков, отсекаемых прямойот осей координат. При этом допускается, чтоилиУравнением (7) может быть задана любая прямая, за исключением прямых, коллинеарных какой-либо из осей координат, а также прямых, проходящих через начало координат.

Упражнение7. Задание прямой в отрезках.

Построить прямую, заданную уравнением L:.

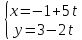Найти ее направляющий вектор и его орт, найти нормальный вектори его орт. Изобразить и пометить данные векторы исходящими из начала координат и из точки.

Отметить отрезки aиb, где прямая отсекает оси координат. Пометить прямуюL.

8. Общее уравнение прямой на плоскости

Если на плоскости фиксирована произвольная декартова прямоугольная система координат OXY, всякое уравнение первой степени с двумя переменнымиxиy определяет относительно этой системы прямую линию.

В самом деле, пусть задано уравнение первой степени

, (9)

в котором A,BиC– любые вещественные числа, причемAиBне равны одновременно нулю. Уравнение заведомо имеет хотя бы одно решение, координаты которой удовлетворяют уравнению (9):

. (10)

Вычитая из уравнения (9) тождество (10), мы получим уже знакомое уравнение (2)

,

эквивалентное уравнению (9).

Числа AиB определяют координаты нормального вектора прямой, т.е. любой ненулевой вектор, перпендикулярный этой прямой.

Частные случаи формулы (9) – неполные уравнения прямой:

1. А = 0,B ≠ 0- уравнение прямой приводится к виду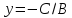. Это уравнение прямой параллельной осиOx; приC = 0 прямаяy = 0 совпадет с осьюOx.

2. B= 0,A ≠ 0- уравнение прямой приводится к виду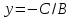. Это уравнение прямой параллельной осиOy; приC = 0 прямаяx = 0 совпадет с осьюOy.

3. C = 0,A ≠ 0, B ≠ 0- уравнение прямой приводится к виду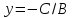. Прямая проходит через начало координат. (ПриA= 0 прямаяy = 0 будет совпадать с осьюOx. ПриB = 0 прямаяx = 0 будет совпадать с осьюOy)

Построение прямой линии по уравнению (1) означает, что входными параметрами в систему MATLABявляются коэффициенты уравнения (1)A,BиC. Поэтому, если B ≠ 0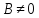,мы всегда можем выразитьyи подать его на вход одноименному аргументу функцииplot(x,y). Для построения прямой будет достаточно двух точек, поэтому аргументxдостаточно задать двумерным массивом, а аргументyбудет вычисляться по формуле, где коэффициентыA,BиCзадаются заранее. Эта формула будет для каждогохвычислять свойу.