3. Уравнение прямой линии, проходящей через данную точку в заданном направлении. Каноническое уравнение прямой на плоскости.

Пусть на плоскости (см. рис.5) заданы декартовая система координат OXY, точкаи ненулевой вектор, гдеkиl- любые действительные числа, неравные нулю одновременно.

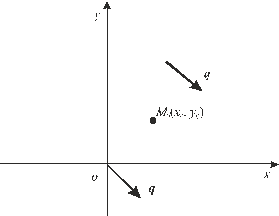
Рис. 5.

Требуется построить прямую L, проходящую через точкупараллельно направлению вектора, и составить ее уравнение.

Рассмотрим вектор , где- любая точка прямойL. Точка M принадлежит прямой L тогда и только тогда, когда , см. рис.6.

Рис.6.

Условие коллинеарности вектора прямой , а, значит, и самой прямой, направляющему вектору- пропорциональность соответствующих координат векторов - даетуравнение прямой линии, проходящей через заданную точку в заданном направлении:

(3)

Уравнение вида (3) называется каноническим уравнением прямой.

Ненулевой вектор называетсянаправляющим векторомпрямой.

Отметим, что в уравнении (3) формально допускается 0 в знаменателе.Это не означает, конечно, что допустимо деление на 0. Формулу (3) следует считать эквивалентом равенства, в которомникакого деления на 0 нет. Уравнения, в которых одна из компонент направляющего вектораравна нулю, называются неполными.

Приведём примеры неполных уравнений прямых линий:

• уравнение определяет прямуюпроходящую через точкупараллельно осинаправляющий вектор прямой.

• уравнение - уравнение оси, прямаяy= 0, проходящая через начало координат; направляющий вектор прямой.

Итак, вместо нормального вектора и точкиположение прямойLна плоскости может быть заданонаправляющим вектором и все той же точкой, см. рис. 7.

Рис.7.

Направляющий вектор прямой ортогонален нормальному вектору прямой.

По виду уравнения прямой вида (2) мы знаем координаты вектора нормали , а из условия ортогональности векторов нормали и направляющего вектора следует, что направляющий вектор будет иметь координаты.

По виду уравнения прямой вида (3) мы знаем координаты направляющего вектора , а стало быть, и координаты нормального вектора.

Упражнение 4. Каноническое уравнение прямой.

Пусть прямая Lпроходит через точкупараллельно направляющему вектору.

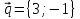
1. Записать каноническое уравнение прямой (см формулу (3)) и сделать его заголовком графика.

2. Входными параметрами сделать координаты kиlнаправляющего вектораи координатыx₀иy₀ точки.

3. Выразить из канонического уравнения y, как функцию отx.

4. Используя функцию plot(), построить прямуюL, сплошную, фиолетового (m) цвета, толщины 2. Значения абсцисс точек прямой –массив, состоящий из двух точек.

5. Пометить прямую L. Отметить на прямой точку.

6. Провести с помощью функции line( ) оси координат черного цвета. Обозначить начало координат.

7. Построить направляющий вектор и орт вектора, берущими начало

а) в начале координат; б) в точке

8. Найти и построить нормальный вектор и орт вектора, исходящими

а) из начала координат; б) из точки _.

4. Уравнение прямой, проходящей через две точки.

Пусть на плоскости (см. рис.8) декартовая система координат OXY, две точкии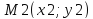. Требуется построить уравнение прямой, проходящей через эти две точки и составить ее уравнение.

Рис.8.

Уравнение этой прямой можно построить, сведя задачу к предыдущей. То есть надо найти направляющий вектор 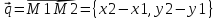,а в качестве точки взять любую из заданных точек, например,.

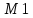
(4)